
- •2. Метрические пространства. Основные примеры. Сходящиеся последовательности и последовательности Коши. Непрерывные и равномерно непрерывные отображения. Условияе Липшица.
- •3. Топология метрического пространства.
- •4. Полные метрические пространства. Примеры полных и неполных пр-в Принцип вложенных шаров.
- •4. Полные метрические пространства. Примеры полных и неполных пр-в Принцип вложенных шаров.
- •5. Теорема Бэра в разных формулировках.
- •6. Продолжение тождеств в метрич пр-вах. Продолжение отображений в метрических пространствах
- •7. Пополнение метрического пространства
- •8. Необходимость пересмотра понятия интеграла.
- •9. Системы подмножеств: кольца, полукольца, алгебра.
- •10.Общее понятие меры. Монотоность, сигма-аддитивность,непрерывность, субаддитивность. Полнота меры,
- •11.Продолженне мера но Лебегу: конструкция(внешняя мера, измеримые множества). Субаддитигзность, критерий измеримости.
- •12. Основная теорема о продолжении меры по Лебегу
- •13. Мера Лебега на отрезке и на прямой: конструкция, множество Кантора. Неизмеримые множества, сравнение измеримых множествс борелевкими.
- •14. Меры Лебега-Стилтьеса: конструкция, мера одноточесного множества, множества меры нуль
- •15. Абсолютная непрерывность меры относительно другой меры. Абсолютные непрерывные функции и порожденные ими меры Лебега-Стилтьеса.Функция Кантора.
- •15. Абсолютная непрерывность меры относительно другой меры. Абсолютные непрерывные функции и порожденные ими меры Лебега-Стилтьеса.Функция Кантора.
- •16. Измеримые функции. Различные типы сходимости. Теорема о пределе последовательности измеримых функций, замкнутость относительно алгебраических операций.
- •17. Простые функции. Приближение измеримых функций простыми.
- •18. Теорема Егорова.
- •19. Интергал Лебега: определение, элементарные свойства, неравенство Чебышева,сравнение с конструкцией интеграла Римана
- •20. Свойство абсолютной обсалютной непрерывности интеграла Лебега
- •21. Теорема Лебега о мажорированной сходимости.
- •22. Теорема б.Леви. Следствие для рядов
- •23. Теорема Фату
- •24. Заряды. Взаимная сингулярность мер и зарядов. Теорема Радон-Никодима. Формула Ньютона-Лейбница.
- •25. Продолжение сигма-конечных мер. Интеграл по сигма-конечной мере.
- •26. Произведение мер. Теорема Фубини.
- •27. Пространство l1(X,m): конструкция‚ метрика, полнота.
- •2. Метрические пространства. Основные примеры. Сходящиеся последовательности и последовательности Коши. Непрерывные и равномерно непрерывные отображения. Условияе Липшица.
7. Пополнение метрического пространства
О
п р е д е л е н и е 1.
Полное метрическое пространство
 называется
называется
 ,
если
,
если
 является его всюду плотным подпространством.
является его всюду плотным подпространством.
Так как изометричные метрические пространства с точки зрения теории метрических пространств считаются одинаковыми, то любое метрическое пространство, изометричное , также будем называть пополнением метрического пространства и и пополнение пространства, изометричного , будем считать пополнением пространства . Как будет показано, из общих соображений следует, что пополнение метрического пространства единственно с точностью до изоморфизма.
Т
е о р е м а 1. (о
пополнении метрического пространства).
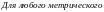
 .
.
Л
е м м а 1.


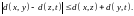
Л
е м м а 2.

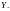

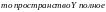 .
.
П
р и м е р 1. Построим
пополнение метрического пространства
из примера 4 лекции3 с помощью конструкции,
описанной в общем виде в теореме о
пополнении. Если
 - последовательность Коши в
,
то есть
- последовательность Коши в
,
то есть
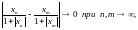
то
последовательности Коши возможны только
трех видов:
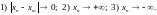 Последовательности Коши первого вида
сходятся, последовательности вида 2) и
3) не сходятся в рассматриваемом
пространстве. Последовательности вида
2) эквивалентны между собой и, следовательно,
образуют один класс эквивалентных
последовательностей, который обозначим
Последовательности Коши первого вида
сходятся, последовательности вида 2) и
3) не сходятся в рассматриваемом
пространстве. Последовательности вида
2) эквивалентны между собой и, следовательно,
образуют один класс эквивалентных
последовательностей, который обозначим
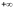 ;
последовательности вида 3) образуют
другой класс, который обозначим символом
;
последовательности вида 3) образуют
другой класс, который обозначим символом
 .
Таким образом, множество
.
Таким образом, множество
 в данном примере состоит их двух точек
и
,
и процесс пополнения пространства
сводится к добавлению двух точек.
Построенное пространство иногда называют
в данном примере состоит их двух точек
и
,
и процесс пополнения пространства
сводится к добавлению двух точек.
Построенное пространство иногда называют
 .
.
В других конкретных примерах построение пополнения с помощью общей конструкции из доказательства теоремы о пополнении приводит к весьма громоздким объектам. Поэтому обычно пополнения стараются строить так, чтобы их элементами были более простые объекты (функции, последовательности и так далее). Например, в лекции 6 будет показано, что пополнение пространства может быть описано более просто – как множество функций, интегрируемых по Лебегу.
8. Необходимость пересмотра понятия интеграла.
 обычно
называют уравнения относительно
неизвестной функции, в которые эта
функция входит под знаком интеграла.
Такое описание не является точным
определением, так как не указано, какие
еще операции допустимы в записи уравнения.
обычно
называют уравнения относительно
неизвестной функции, в которые эта
функция входит под знаком интеграла.
Такое описание не является точным
определением, так как не указано, какие
еще операции допустимы в записи уравнения.
Ограничимся рассмотрением интегральных уравнений вида
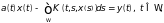
где
 - некоторое пространство с мерой;
- некоторое пространство с мерой;
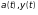 - заданные на
функции;
- заданные на
функции;
 -
-
заданная
на
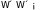 функция;
функция;
 - неизвестная функция. Чаще всего в
качестве
рассматривается некоторое подмножество
в
- неизвестная функция. Чаще всего в
качестве
рассматривается некоторое подмножество
в
 с
мерой Лебега, например, отрезок
с
мерой Лебега, например, отрезок
 .
Решение
ищется в различных пространствах
функций, определенных на
,
в зависимости от свойств функций
и
.
Решение
ищется в различных пространствах
функций, определенных на
,
в зависимости от свойств функций
и
 .
В случае, когда рассматриваются
непрерывные функции, интеграл можно
понимать в смысле Римана. Заметим, что
пространства выбираются так, чтобы для
функций из этого пространства интеграл
в уравнении существовал.
.
В случае, когда рассматриваются
непрерывные функции, интеграл можно
понимать в смысле Римана. Заметим, что
пространства выбираются так, чтобы для
функций из этого пространства интеграл
в уравнении существовал.
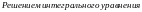 (записанного
выше) называется функция
(записанного
выше) называется функция
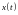 ,
при подстановке которой в уравнение
выполняется равенство для всех
,
при подстановке которой в уравнение
выполняется равенство для всех
 или почти всех
или почти всех
 .
.
К исследованию интегральных уравнений приводит, например, решение задачи Коши для обыкновенного дифференциального уравнения:

Проинтегрировав
на отрезке
 данное дифференциальное уравнение с
учетом начального условия, получаем
интегральное уравнение
данное дифференциальное уравнение с
учетом начального условия, получаем
интегральное уравнение

которому удовлетворяет решение задачи Коши.
Выделим
некоторые классы интегральных уравнений.
Интегральное уравнение будем называть
 ,
если функция
,
если функция
 линейна по
линейна по
 ,
то есть имеет вид
,
то есть имеет вид
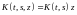 .
Линейное интегральное уравнение имеет
вид
.
Линейное интегральное уравнение имеет
вид

Функция
двух переменных
 называется
называется
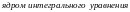 .
.
Если
 ,
то линейное интегральное уравнение
называют
,
то линейное интегральное уравнение
называют
 ,
а при
,
а при
 -
-
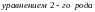 .
При произвольном
.
При произвольном
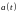 данное уравнение обычно называют
данное уравнение обычно называют
 .
Таким образом, уравнение 1-го рода имеет
вид
.
Таким образом, уравнение 1-го рода имеет
вид
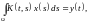
уравнение
2-го рода -

