5. Теорема Бэра в разных формулировках.

Th.1:

Пусть (X,p) – полное метрическое пр-во, U_k-последовательность открытых всюду плотных множеств. Тогда пересечение U= _k является всюду плотным множеством.

Th.2:

Пусть (X,p) – полное метрическое пр-во, F_k-такая последовательность замкнутых множеств в X, что Х= _k. Тогда хотя бы одно из множеств F_k содержит открытый шар.

Def:

Мн-во А называется нигде не плотным, если его замыкание не содержит ни одного открытого шара.

Следствие:

Полное метрическое пр-во не может быть представлено в виде объединения счетного числа нигде не плотных множеств.

6. Продолжение тождеств в метрич пр-вах. Продолжение отображений в метрических пространствах

Пусть и - метрические (или топологические) пространства, - подмножество и - заданное на непрерывное отображение. Требуется найти непрерывное отображение такое, что для , или доказать его существование. Отображение называется .

Заметим, что задача продолжения не всегда имеет решение.

П р и м е р 1. Если и , то не существует непрерывной на функции , совпадающей с при (функцию нельзя доопределить в нуле так, чтобы она стала непрерывной).

Ясно также, что, вообще говоря, продолжение может быть не единственным. Поэтому представляют интерес теоремы о существовании и о единственности продолжения. Наиболее простой случай, который рассмотрен ниже, связан с продолжением функции с некоторого подмножества на его замыкание.

Т е о р е м а 1.

С л е д с т в и е 1. (о продолжении тождеств).

П р и м е р 2. Пусть и . Последовательности и эквивалентны и являются последовательностями Коши. Но последовательность не является последовательностью Коши и не эквивалентна последовательности . Это является следствием того, что функция не является равномерно непрерывной.

Более сильным условием , чем равномерная непрерывность, является условие Липшица.

О п р 1. Говорят, что отображение , если существует такая постоянная , что для любых выполняется неравенство

Отображение , удовлетворяющее условию Липшица, является равномерно непрерывным, а равномерно непрерывное отображение является непрерывным. Обратное, вообще говоря, неверно.

П р и м е р 3. Числовая функция на непрерывна, но не является равномерно непрерывной.

П р и м е р 4. Числовая функция на равномерно непрерывна, но не удовлетворяет условию Липшица.

Т е о р е м а 2.

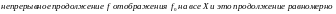
П р и м е р 5. Пространство . Стандартное счетное всюду плотное множество в - множество рациональных чисел.

П р и м е р 6. Пространство . Счетным всюду плотным множеством в этом пространстве является множество полиномов с рациональными коэффициентами.

П р и м е р 7. Пространство . Счетным всюду плотным множеством является множество финитных последовательностей с рациональными координатами, то есть последовательностей вида , где .