40. Метод симметричных составляющих в трехфазных цепях

Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их работы, в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют симметричными составляющими. Различают симметричные составляющие прямой, обратной и нулевой последовательностей, которые различаются порядком чередования фаз.

Симметричную систему прямой последовательности образуют (см. рис. 1,а) три одинаковых по модулю вектора  и  со сдвигом друг по отношению к другу на  рад., причем  отстает от , а   от .

 

Введя, оператор поворота , для симметричной системы прямой последовательности можно записать

.

Симметричная система обратной последовательности образована равными по модулю векторами  и  с относительным сдвигом по фазе на  рад., причем теперь  отстает от , а  - от  (см. рис. 1,б). Для этой системы имеем .

Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (1,в): .

Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно,

Таким образом, получена система из трех уравнений относительно трех неизвестных , которые, следовательно, определяются однозначно. Для нахождения  сложим уравнения (1)…(3). Тогда, учитывая, что , получим

Для определения  с соотношением (1) складываем уравнения (2) и (3), предварительно умноженные соответственно на  и . В результате имеем:

Формулы (1)…(6) справедливы для любой системы векторов , в том числе и для симметричной. В последнем случае .

В заключение раздела отметим, что помимо вычисления симметричные составляющие могут быть измерены с помощью специальных фильтров симметричных составляющих, используемых в устройствах релейной защиты и автоматики.

41. Механические характеристики ад.

Л юбой электродвигатель является частью машинного агрегата, поэтому механические свойства электродвигателей и рабочих машин должны соответствовать друг другу. Эти свойства определяются их механическими характеристиками, т.е. зависимостями вращающего момента электродвигателя от скольжения (угловой скорости, частоты вращения).

Из характеристики М=f(S) видно, что рабочей (устойчивой) ее частью является участок, заключенный между точками 0 и М_т. На этом участке при изменении нагрузки на валу двигатель автоматически переходит из одного установившегося состояния в другое. При увеличении нагрузки скольжение двигателя возрастает, двигатель увеличивает электромагнитный момент, т. е. принимает на себя нагрузку. Если нагрузочный момент превысит максимальный, двигатель останавливается. При уменьшении нагрузки на валу двигателя скольжение уменьшается и одновременно уменьшается электромагнитный момент.

Участок характеристики М=f(S), заключенный между точками М_т и М_п является неустойчивой частью характеристики, так как при увеличении нагрузки скольжение возрастает, а момент двигателя уменьшается и он останавливается. При уменьшении нагрузки скольжение уменьшается, а момент возрастает. Следовательно, частота вращения ротора увеличивается, и режим работы двигателя переходит на устойчивую часть характеристики.

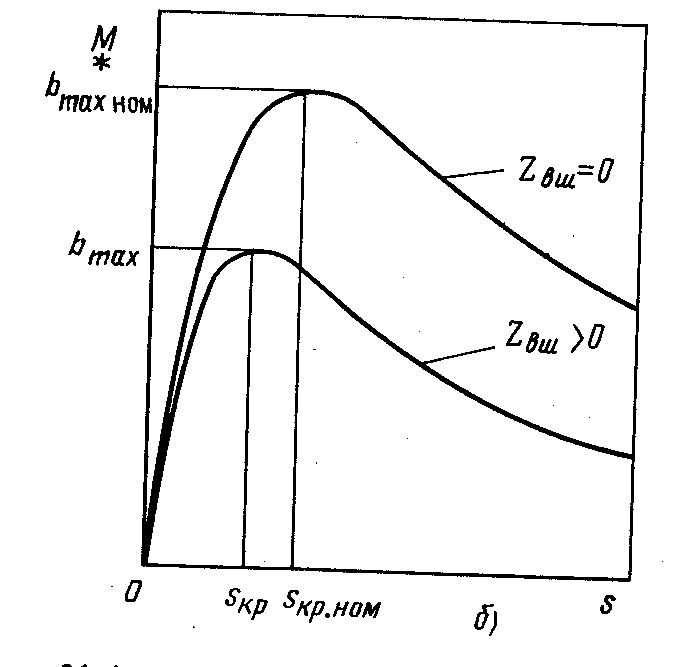
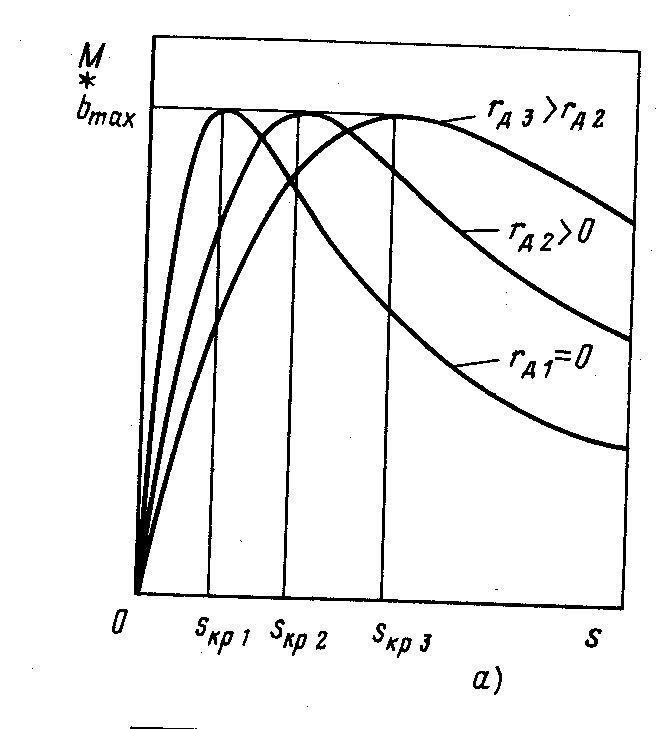
Рисунок – Механические характеристики АД при разных значениях сопротивления: а – активного, включенного в цепь ротора; б – внешнего в цепи статора.