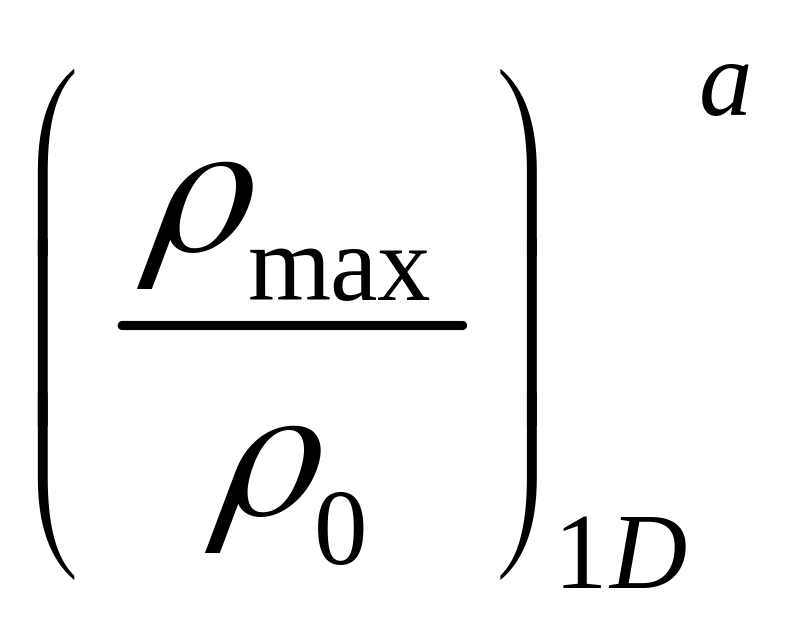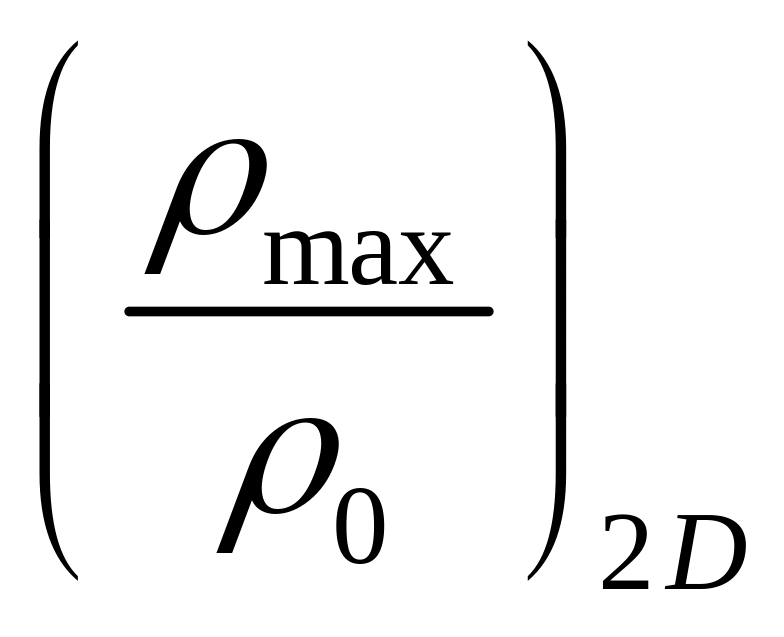4.1. Эволюция теплового разрыва

Рассмотрим задачу распространения тепловой волны в однородной неподвижной среде. Это хорошо известный тест на способность численной схемы рассчитывать тепловые скачки. Первоначальная модель включала 57 908 частиц, равномерно распределенных по квадратной решетке так, что плотность получается равной . -образный скачок внутренней энергии порождает фронт тепловой волны, который эволюционирует по закону:

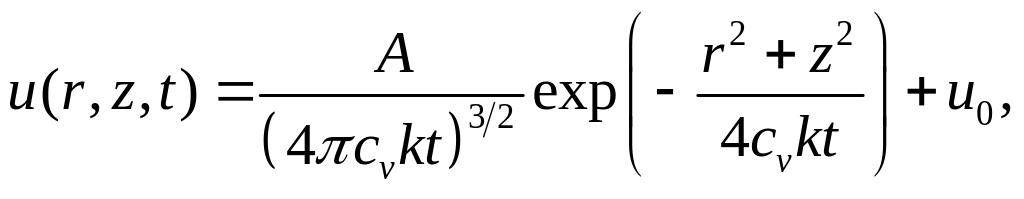(52)

где – удельная теплоемкость, а – коэффициент теплопроводности. Был принят следующий набор значений: , , а . Профиль начальной внутренней энергии задан уравнением (52) при , которое было принято за начальное время ( ) для расчета по методу SPH. Тогда эволюция тепла следует уравнению теплопроводности (35).

На рис. 4 (слева) представлены профили тепловой волны на различные моменты времени. Как можно заметить, они прекрасно согласуются с аналитическим решением (52). С течением времени амплитуда волны и угол наклона уменьшаются из-за диффузии тепла. Первоначальный разрыв быстро размывается в результате диффузии тепла, и вскоре появляется тепловая волна, направляющаяся вправо, которая выравнивает внутреннюю энергию системы. В момент времени график уже довольно плоский, а система недалека от состояния теплового равновесия. В этот момент суммарная энергия сохраняется с точностью до . На рис. 4 (справа) показана эволюция тепловой волны, получающейся после удаления первого члена в правой части уравнения (35). Как видим, она уже не согласуется с решением по методу SPH. Поэтому этот член очень важен, особенно в расчетах с сильными тепловыми градиентами вблизи оси симметрии.

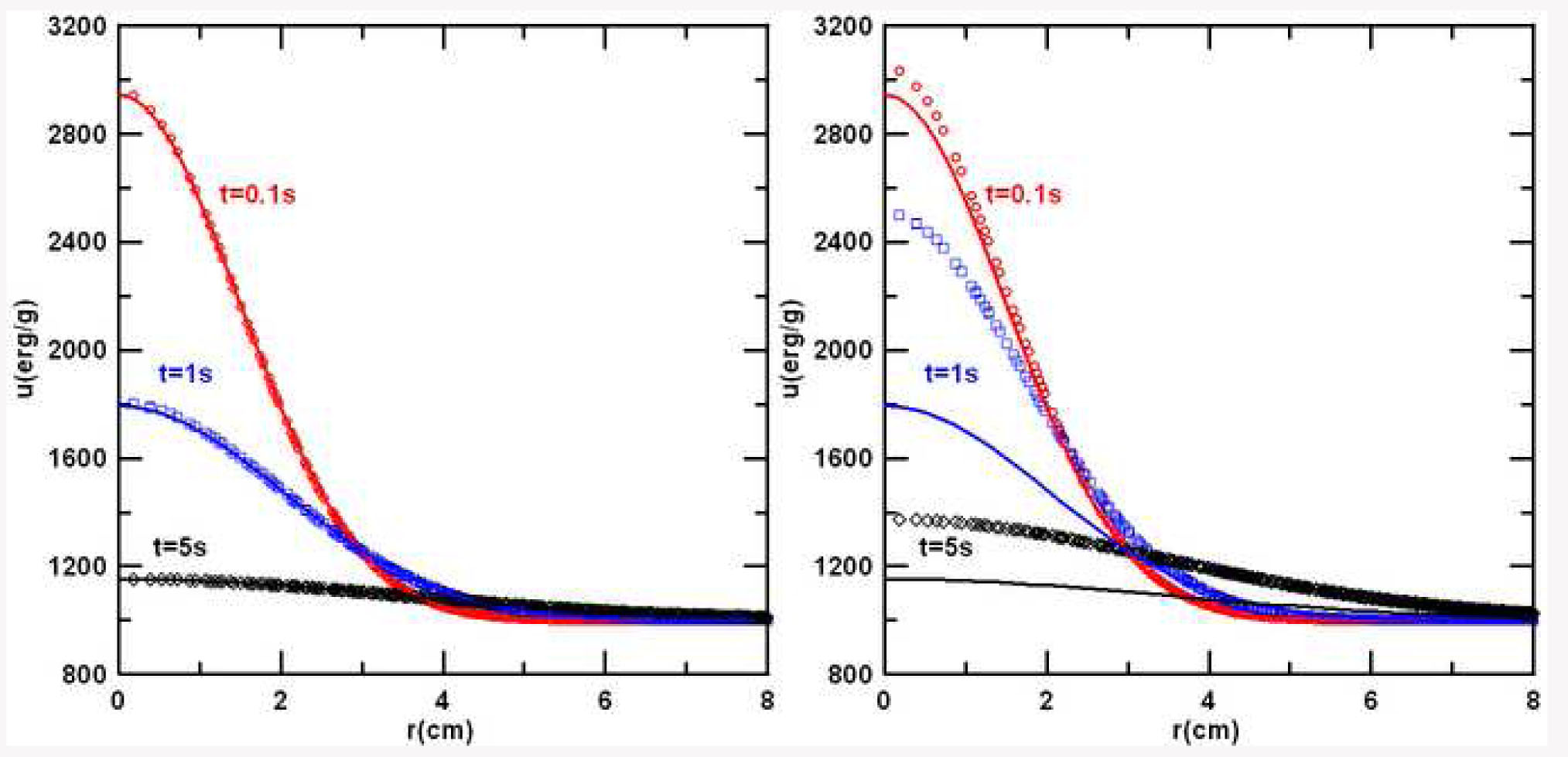
Рис.4 Эволюция теплового разрыва, первоначально заданного в окрестности оси симметрии. График внутренней энергии в различные моменты времени хорошо воспроизводится методом SPH, если учитывается член окружного напряжения (график слева). Однако если этот член игнорируется, результаты не ложатся на кривые аналитических решений, представленных сплошной линией (график справа).

4.2. Гравитационный коллапс политропы

Во втором тесте рассматривается катастрофический, хотя и весьма неправдоподобный астрофизический сценарий. Сферически-симметричная солнцеподобная политропа внезапно выходит из состояния равновесия из-за потери 20% своей внутренней энергии, в результате чего структура коллапсирует под действием силы гравитации. В некоторой точке коллапс останавливается, и формируется ударная волна аккреции, в результате которой часть массы политропы сбрасывается. Затем следует несколько эпизодов сжатия, сопровождающихся потерей массы, пока звезда не достигает нового состояния равновесия. Хотя данный сценарий и не реалистичен, он включает несколько интересных физических явлений, так как аккреционные ударные волны и пульсирующие неустойчивости весьма распространены в астрофизике. Поскольку первоначальная модель обладает сферической симметрией, мы рассчитываем, что она сохранит ее во время имплозии и последующего отражения от центра. Сохранение сферической симметрии – это важный тест для многомерных гидрокодов в тех случаях, когда имеются эпизоды с сильным торможением. В случае осесимметричной гидродинамики, более высокий численный шум вблизи оси симметрии может инициировать рост конвективных неустойчивостей. Использование в качестве начальной модели сферически симметричной имеет то дополнительное преимущество, что эволюцию, рассчитанную при помощи кода SPH, можно проверить, используя стандартную лагранжеву гидродинамику с одним измерением.

Первоначальной моделью являлась сферически симметричная политропа с индексом Радиус был положен равным так что центральная плотность составила После того, как была построена одномерная модель равновесия, она была преобразована в двухмерное распределение 51 408 частиц, размещенных на прямоугольной решетке. Масса частиц была подогнана таким образом, чтобы она воспроизводила профиль плотности политропы.

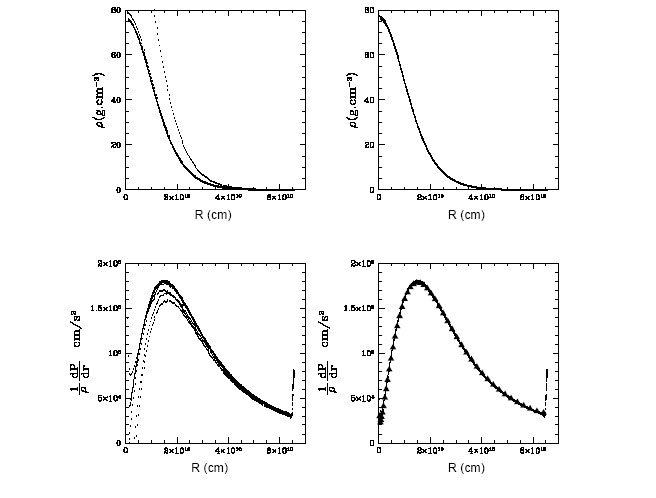
Рис 5. Профили плотности, гравитации и градиента давления политропы. Верхний ряд: профиль плотности с осевыми коррекциями (справа) и без них (слева). Нижний ряд: то же самое для градиента давления. Абсолютное значение силы гравитации, рассчитанное с использованием градиента гравитационного потенциала, полученного из уравнения (45), отмечено закрашенными треугольниками (нижний ряд, справа). Представлены все массовые частицы политропы. Игнорирование осевых коррекций усиливает дисперсию профилей.

На рис. 5 показаны профили плотности и градиента давления при вычисленные с использованием двухмерного метода SPH. Как видим, включение коррекционного члена заданного уравнением (5), в уравнение импульса оказывается решающим для получения профилей этих величин, достаточно хороших, чтобы гарантировать устойчивость первоначальной модели. В политропу было внесено возмущение путем повсеместного уменьшения температуры на 20% по сравнению со значением, отвечающим состоянию равновесия. После этого при помощи двухмерного метода SPH мы проследили эволюцию от имплозии до первой пульсации и сравнили ее с эволюцией, полученной при помощи одномерного лагранжева гидрокода. Основные характеристики модели и краткие выводы приведены в таблице 1.

Таблица 1. Основные характеристики тестовых моделей, описанных в разделах 4.2 и 4.3. Сохранение импульса представлено центром перемещения массы и поделенным на радиус структуры в данный момент времени (столбцы 5 и 6). Сохранение импульса и энергии соответствует последней рассчитанной модели, приведенной на рис. 6-9.

Тест	Число частиц
Политропа	51408	2,43	2,49
Имплозия капсулы	30448	29	32
Тест Ноха	50334	64	58
Столкновение газовых облаков	55814	–	–

Аналитическое значение для теста Ноха.

Вскоре после того, как модель была дестабилизирована, политропа начала коллапсировать. В момент времени был достигнут максимум центральной плотности Подобный максимум был получен с использованием одномерной гидродинамики. Профили плотности и радиальной скорости в различные моменты времени представлены на рис. 6. Как можно увидеть, эволюции, рассчитанные в одном и двух измерениях, очень схожи и, в целом, обе кривые очень хорошо согласуются между собой. В последний момент времени, вошедший в наши расчеты, ударная волна уже прорывает поверхность политропы. Вскоре после этого с поверхности выбрасывается некоторое количество массы, и, как показывает одномерный расчет, для звезды наступает долгая стадия пульсации, которая длится до наступления следующего состояния равновесия.

Таким образом, численная схема оказалась пригодной для работы с таким сценарием. Алгоритм, призванный вычислять силу гравитации по уравнению (45), который основан на прямом взаимодействии между кольцами (рис. 2), продемонстрировал свою эффективность на практике. Модуль искусственной вязкости смог сохранить траекторию ударных волн, хотя на некоторых стадиях в послеударной области наблюдались небольшие паразитные колебания. Эти численные колебания на профиле скорости отчетливо видны на рис. 6 в момент времени В трех последних столбцах таблицы 1, содержится информация, касающаяся сохранения импульса и энергии в нашей последней модели в момент времени Наблюдалось превосходное сохранение импульса, близкое к точности компьютера, в то время, как сохранение энергии было более скромным, всего С другой стороны, сферическая симметрия также достаточно хорошо сохранялась во время расчетов. К отрицательным моментам можно отнести то, что двухмерные вычисления систематически запаздывали по сравнению с одномерными. Относительный сдвиг во времени оставался примерно постоянным, около на протяжении всей эволюции. Для большей ясности, временные отрезки на рис.6 были взяты из моделирования по методу SPH, а временные отрезки одномерной эволюции выбирались так, чтобы соответствовать двухмерным профилям.

о

радиус

о

радиус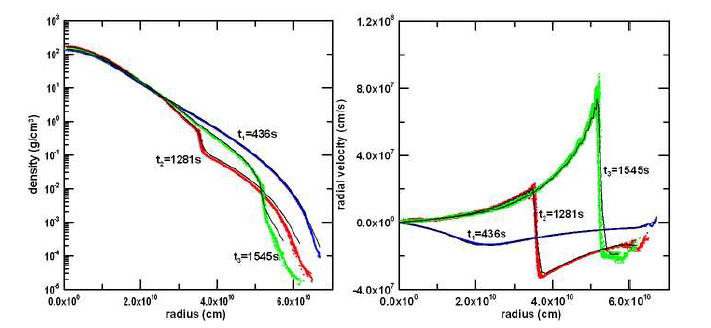

Рис. 6 Профиль плотности (слева) и радиальная скорость (справа) во время имплозии и последующего отражения от центра в различные моменты времени. Черная сплошная линия представляет собой профиль, вычисленный с использованием одномерного гидрокода такого же разрешения. В момент времени ударная волна пробивает поверхность звезды. На рисунке показаны все частицы, используемые при расчетах.