4. Тестовые примеры

В этом разделе мы опишем и обсудим в подробностях пять тестовых примеров с целью проверки расчетной схемы, изложенной в четырех предыдущих разделах. В первом тестовом примере рассматривается распространение теплового скачка, возникающего на оси симметрии. Этот случай хорошо изучен и имеет аналитическое решение, удобное для сравнения. Три расчета: гравитационный коллапс политропы, имплозия однородной капсулы и задача о взаимодействии с преградой ударной волны – связаны с имплозией сферически-симметричных систем. Хотя на первый взгляд такое ограничительное условие кажется слишком жестким, на самом деле оно таковым не является, так как сферическая симметрия не является естественной геометрией для осесимметричных систем, описанных в цилиндрических координатах. Любое отклонение от чисто сферической геометрии во время имплозии будет инициировать рост гидродинамических неустойчивостей. Поэтому, сохранение симметрии во время расчета является важным условием, которое следует добавить к сохранению массы, импульса и энергии. Наконец, последний тест был разработан с целью моделирования столкновения двух пузырей жидкости, движущихся вдоль оси Z.

Первоначальные модели рассчитывались при помощи отображения сферически симметричных профилей на двухмерное распределение частиц, расположенных на квадратной решетке. Масса частиц была подогнана таким образом, чтобы она воспроизводила кривую плотности одномерной модели. Например, чтобы получить модели с постоянной плотностью, брались массы, пропорциональные координате частицы по оси r. Вдоль оси z были введены граничные условия зеркальной симметрии с использованием зеркальных частиц-призраков. В тесте, моделирующем коллапс политропы, использовалось уравнение идеального газа с с излучением, а во всех остальных тестах – только уравнение идеального газа. Мы использовали регулируемый параметр длины сглаживания , который обновлялся на каждом этапе так, чтобы число соседей внутри круга радиусом оставалось постоянным и равным . Интерполяционным ядром являлся кубический сплайн. Численное интегрирование гидродинамических уравнений SPH выполнялось с использованием двушаговой центрированной схемы со вторым порядком точности.

Стоит отметить, что в тесте со свободным падением однородной сферы, скорость обновлялась с использованием XSPH варианта метода (где X обозначает некоторую отфильтрованную величину), предложенного Monaghan в 1989 году, чтобы избежать проникновения частиц за ось симметрии. В этом частном случае массовые частицы при малых радиусах более склонны пересекать ось Z, так как давление и силы вязкости искусственно полагались равными нулю. Поэтому любое остаточное значение гравитации может заставить частицы, расположенные близко к центру, принять физически невозможные значения . Мы скорректировали только r-компоненту скорости, используя следующее выражение:

(50)

где – новая более гладкая скорость. Параметр является переменным.

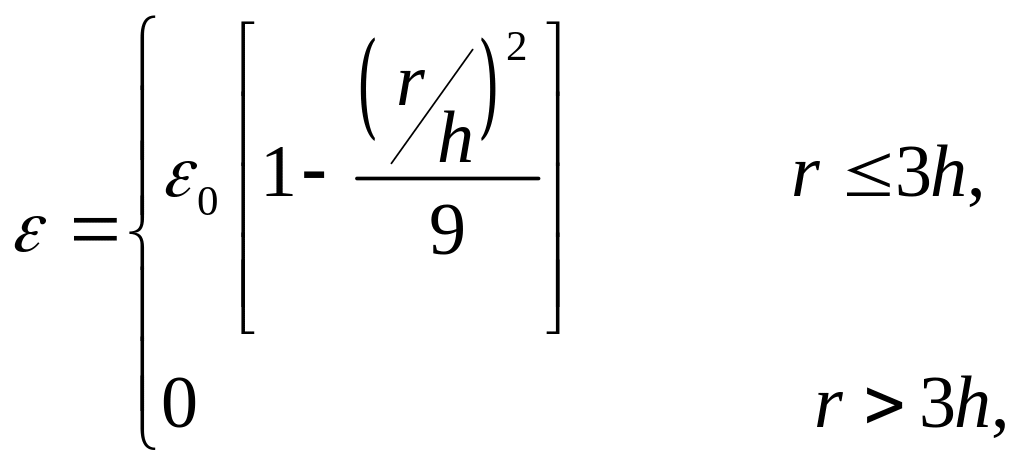(51)

где . Использование варианта метода XSPH для движения частиц навязывает ограничение при и не дает частицам пересекать ось.