3.3.1. Коллапс однородных газовых структур при свободном падении. Вращение

В качестве первичной проверки алгоритма гравитации, основанного на уравнении (45), мы смоделировали коллапс сферы с однородной плотностью, массой и радиусом при свободном падении. Это стандартный тест, который имеет следующее аналитическое решение:

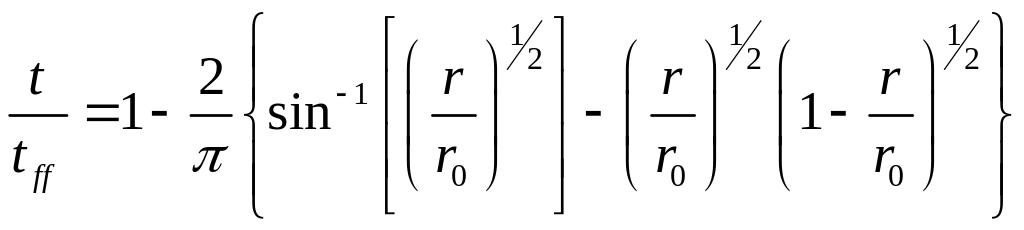, (46)

где – начальное положение элемента жидкости, а . Время свободного падения равно:

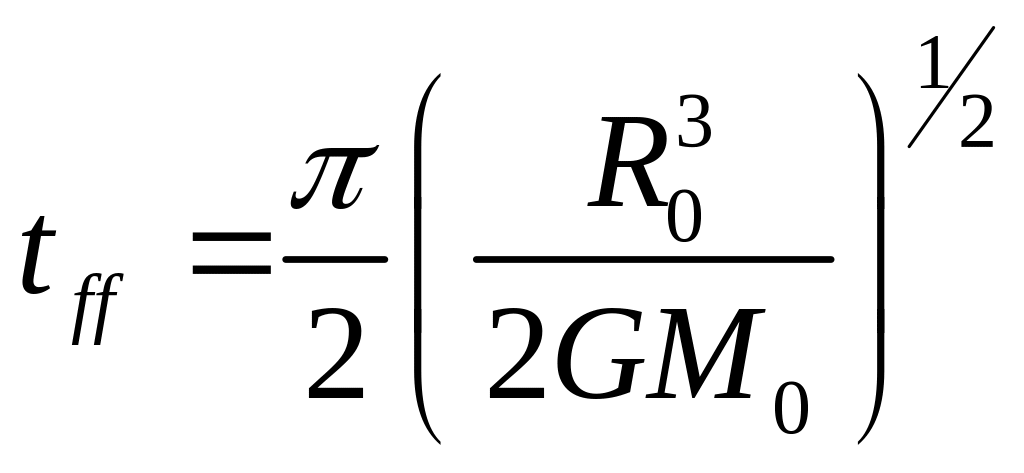. (47)

Мы строим однородную сферу с и , заполненную частицами, которые располагаются в квадратной решетке. Давление газа и искусственная вязкость полагались равными нулю, так что структура коллапсировала под действием гравитационных сил. После этого последовала имплозия, которая продолжалась до момента времени, близкого к . Хотя тест свободного падения ограничен сферически симметричной геометрией, он достаточно эффективен, так как эволюция в высокой степени нелинейна, что обеспечивает хорошую проверку как модуля расчета гравитации, так и схемы интегрирования (подробнее в следующем разделе). На рис. 3 изображена эволюция частицы, находящейся в начальный момент времени в точке . Как видим, эволюция хорошо согласуется с аналитическим решением, представленным формулой (46).

Однородная сфера

Однородный цилиндр

Однородный вращающийся цилиндр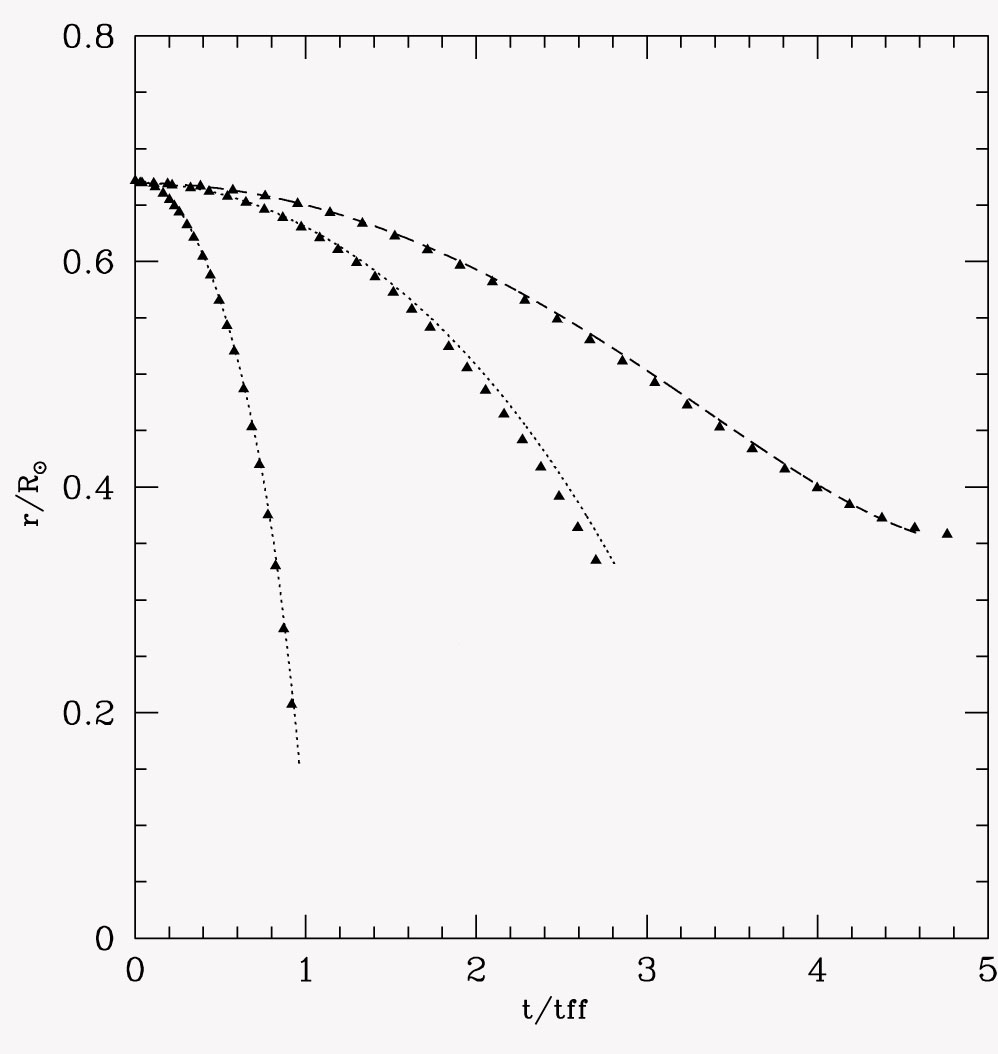

Рис.3 Тест свободного падения. Треугольниками отмечены аналитические решения для каждого случая. Первоначальный радиус частицы , для всех случаев.

Один из вопросов, особенно интересующих астрофизиков – это способность осесимметричных кодов SPH оперировать с вращением. Тема далеко не тривиальна, поскольку в целом она включает перенос вращательного момента за счет вязкого сцепления. Хотя окончательный ответ на этот вопрос не входит в задачи нашего исследования, есть один случай, который может быть рассмотрен в рамках приведенной схемы: быстрая имплозия (или разлет) вращающегося самогравитирующего облака. Если характерное динамическое время существенно меньше, чем время вязкого взаимодействия, для решения задачи можно навязать условие сохранения углового (вращательного) момента вокруг оси симметрии. Мы собираемся просто добавить центробежную силу, которая возникает из конечного вращательного момента, к r-компоненте гравитации.

В качестве примера мы смоделировали коллапс тонкого вращающегося газового цилиндра с однородной плотностью и центром в начале координат. Начальные координаты определены массой радиусом и длиной цилиндра . Если мы положим условие твердотельного вращения, то удельный вращательный момент частицы задается формулой , где – начальная скорость вращения цилиндра , а – положение элемента жидкости в начальный момент времени . Сохранение вращательного момента требует выполнения равенства , поэтому центробежная сила равна , и это выражение прибавляется к первой компоненте гравитации, вычисленной, по уравнению (45), для получения эффективного значения гравитации. Как и в случае сферического коллапса, мы взяли и , в то время как длина цилиндра была равна . Эволюция частиц массы прослеживалась для двух значений вращательного момента: (1) нулевой вращательный момент и (2) , где , для которого центробежная сила равна половине силы гравитации в этой точке. В этом случае мы использовали большое количество частиц, , чтобы уменьшить граничные эффекты.

С другой стороны, полагая и используя закон Гаусса, можно разработать аналитический подход к вышеназванному сценарию. Уравнение для ускорения приобретает вид:

, (48)

где , а – значение гравитации при . Согласно закону Гаусса, , но лучше взять непосредственно из расчета по SPH, чтобы обеспечить одинаковые начальные условия для обоих расчетов. Решение уравнения (48) примет вид:

, (49)

оно решается численно при заданных и .

На рис. 3 изображена эволюция частицы, находящейся в начальный момент времени в точке , без начального вращательного момента и с ним, а также с вращательным моментом, полученным с использованием аналитического подхода из уравнения (49). В случае с нулевым вращательным моментом мы получаем свободное падение частицы, которое оказалось не таким сильным, как в сферическом случае, благодаря более низкой начальной плотности цилиндра. Как можно увидеть на рис. 3, аналитические результаты согласуются с результатами метода SPH не так хорошо, как в сферическом случае для . Это и не удивительно, так как граничные эффекты на ребрах цилиндра все больше влияют на гравитацию в контрольном положении частицы, а ее эволюция очень чувствительна к небольшим изменениям силы гравитации.

При добавлении цилиндру вращательного момента при с, имплозия структуры замедлилась. Как было упомянуто выше, мы подбирали величину вращательного момента таким образом, чтобы вклад центробежной силы при был равен половине силы гравитации в этой точке. Как можно увидеть на рис. 3, результат моделирования согласуется с аналитическими результатами лучше, чем в случае «чистого» свободного падения. Это связано с тем, что на эволюцию влияет не только гравитация, а из-за конечного размера вращающегося цилиндра погрешности не так сильно сказываются на конечном результате, как в случае невращающегося цилиндра. В момент времени элемент жидкости начинает поддерживаться центробежной силой, что хорошо согласуется с аналитической оценкой.