3.3. Самогравитация

В настоящее время в двухмерных гидрокодах часто учитывают гравитацию с помощью решения уравнения Пуассона или, если система остается близкой к сферически-симметричной, просто рассчитывая лагранжеву массу, заключенную в сферу, ниже рассматриваемой точки, и используя закон Гаусса. Методы, основанные на решении уравнений Пуассона, доказали свою пригодность для определения гравитации в эйлеровой гидродинамике, где для расчета гравитации может использоваться та же сетка, которая используется для расчета движения элементов жидкости. Однако, они испытывают затруднения с определением внешних граничных условий, что связано с бесконечным радиусом действия силы гравитации. В лагранжевых бессеточных методах, таких, как метод SPH, для вычисления гравитации лучше использовать взаимодействие между самими частицами. Оценка гравитационной силы через прямое взаимодействие частицы с частицей приводит к схеме, что оставляет возможность расчета только для небольшого числа частиц. При больших N, что часто требуется при трехмерных расчетах, приходится полагаться на приближенные схемы, основанные, например, на методах иерархического дерева Hernquist & Katz (1989). Однако в двумерном осесимметричном случае иерархические методы работают недостаточно эффективно, так как то, что мы называем частицами, на самом деле является кольцами различного размера. Обычно отношение радиуса этих колец к расстоянию до точки, в которой необходимо вычислить силу, слишком велико, чтобы можно было применить мультиполярный подход для оценки гравитационной силы. К счастью, хорошее разрешение, обычно достигаемое в двухмерных кодах при использовании приемлемого числа частиц, позволяет выполнить расчет напрямую.

Согласно Рис.2, гравитационная сила на единицу массы в точке P с координатами (где Z – ось симметрии) с учетом кольцевой структуры имеет следующий вид:

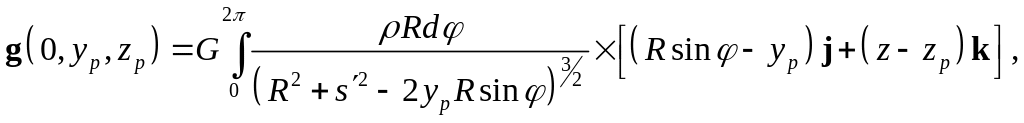(36)

где смысл символов ясен из рис. 2. Гравитационная сила, действующая на частицу, может быть записана в виде:

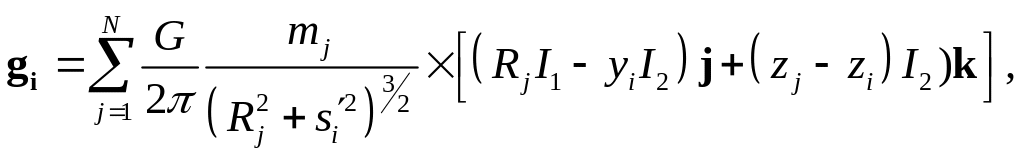(37)

где а - масса частицы, ассоциируемая с кольцом j.

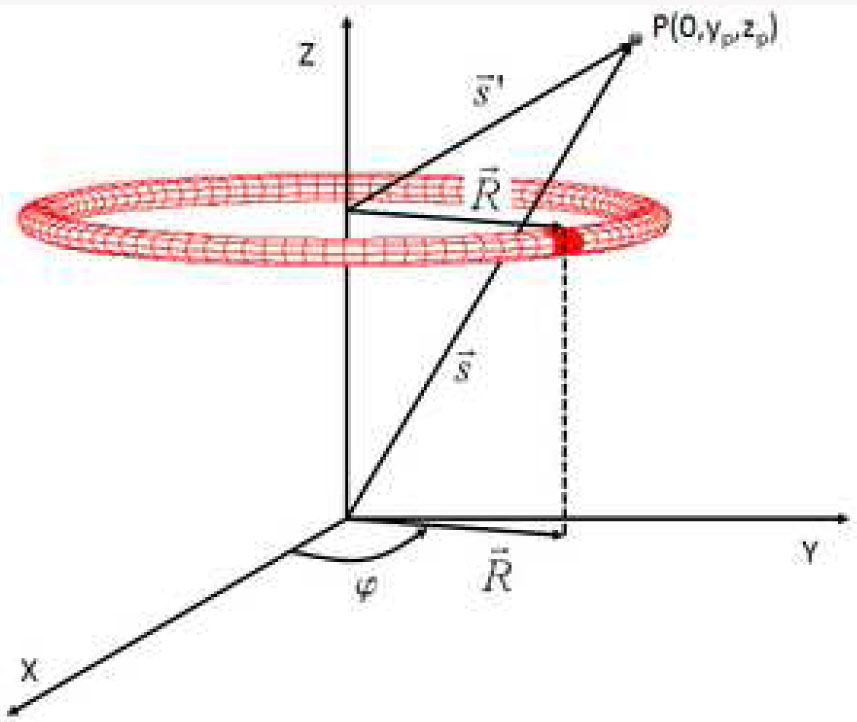
Рис.2 Система координат и условные обозначения, используемые для описания гравитации.

Интегралы и определяются следующим образом:

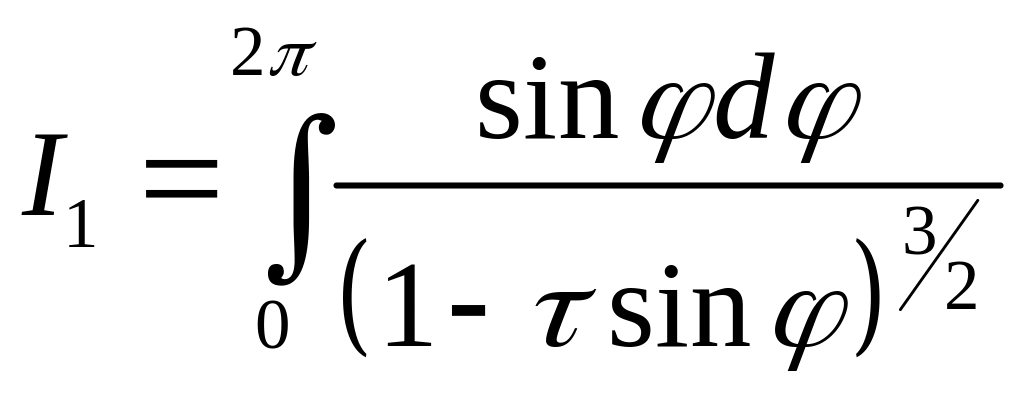(38)

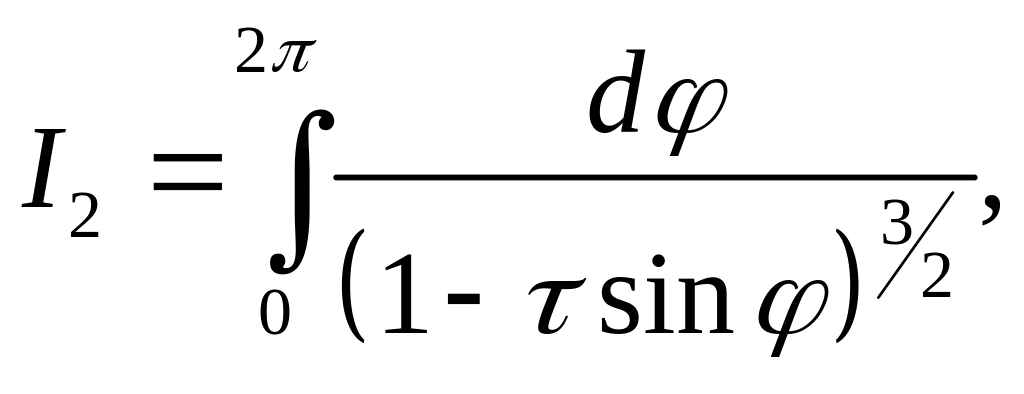(39)

где параметр равен:

(40)

Хотя эллиптические интегралы и нельзя вычислить аналитически, их можно затабулировать как функции от параметра определенного в уравнении (40). Легко показать, что значение всегда находится внутри интервала хотя при интегралы и становятся расходящимися. Таким образом, силу гравитации можно успешно вычислить по следующей схеме.

1. Составить таблицу для интегралов и как функций от . Достаточно будет построить таблицу с 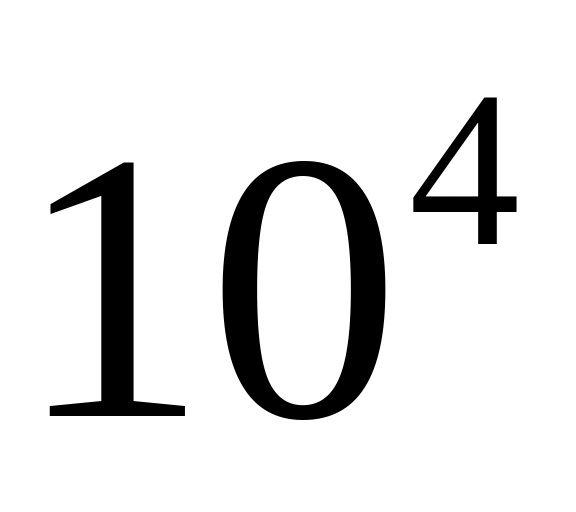строками, в которых аргументы равномерно распределены в интервале

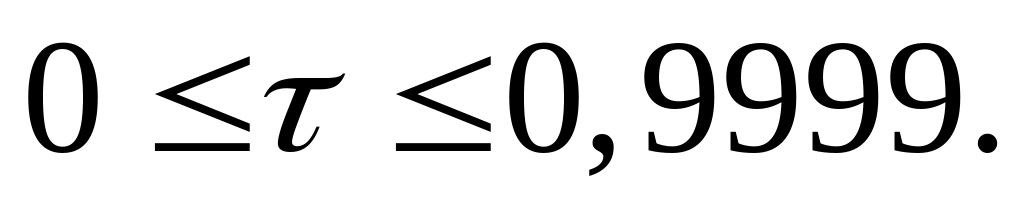
2. Для ускорения счета не обязательно интерполировать по таблице, достаточно взять число, расположенное ближе всего к значению , найденному по формуле (40).

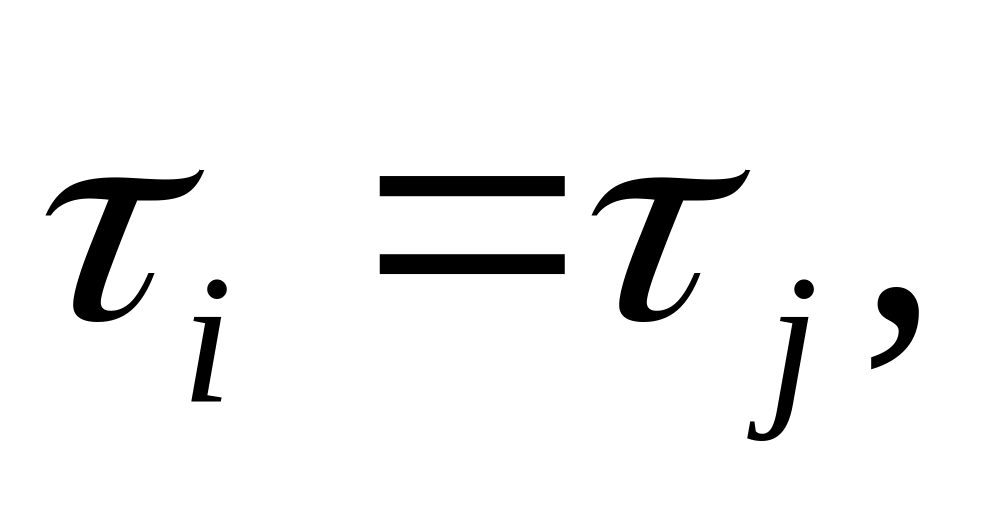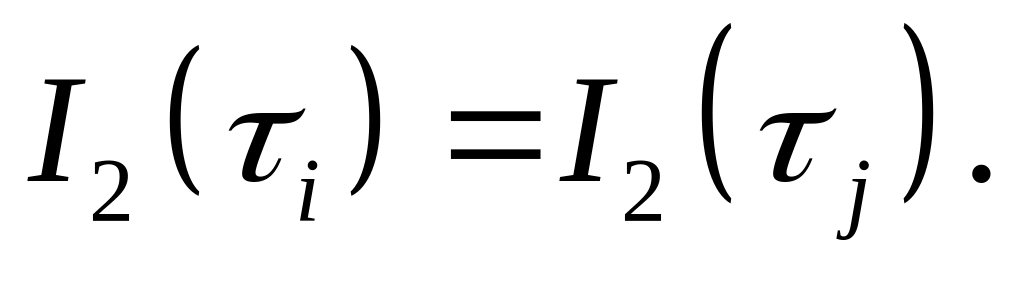3. Заметим, что параметр симметричен относительно любой пары частиц, так что и Поэтому вычислять достаточно только половину значений.

Если алгоритм оптимизирован, такая схема позволяет достаточно точно учесть гравитацию для десятков тысяч частиц. Во многих приложениях для обеспечения хорошего разрешения достаточно использовать частиц в двух измерениях.

Другой интересующей нас физической величиной является гравитационный потенциал в месте нахождения i-частицы. Легко показать, что вклад кольца j в гравитационный потенциал находится по формуле

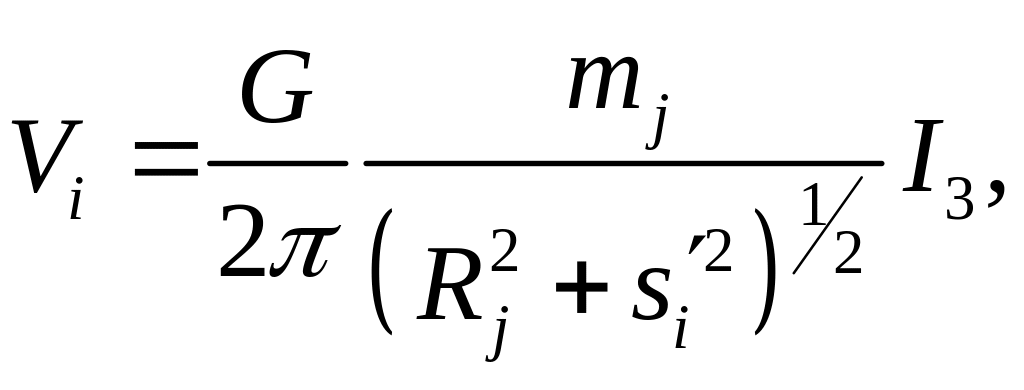(41)

где

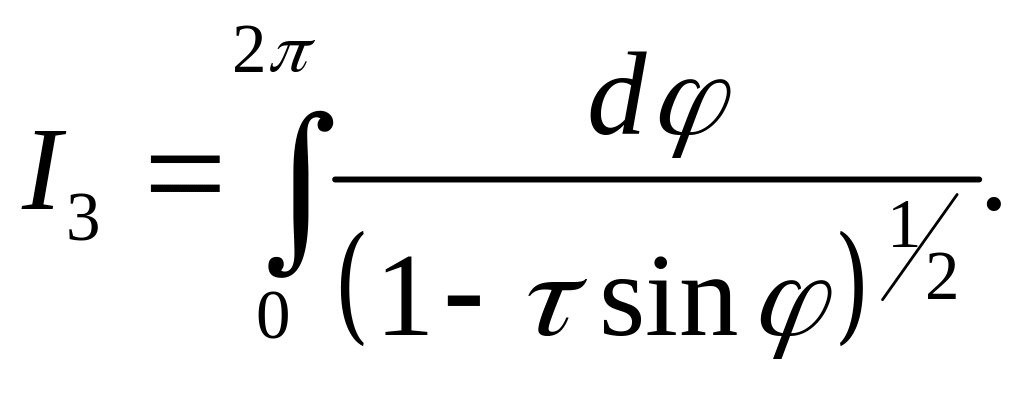(42)

Описанную выше процедуру для вычисления силы можно также с успехом использовать для нахождения С другой стороны, точное вычисление гравитационного потенциала позволяет вычислить силу гравитации, взяв градиент V в любой точке.

(43)

Форма, больше подходящая для расчетов по методу SPH, может быть получена с использованием формулы

(44)

которая, в соответствии с уравнениями (7) и (9), ведет к следующему дискретному уравнению:

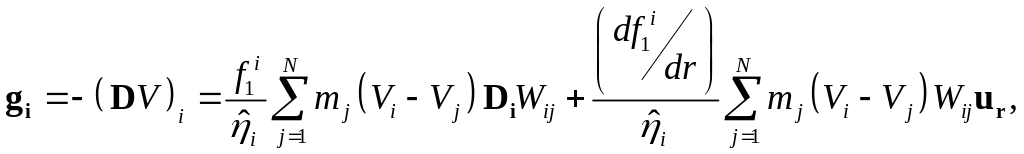(45)

где – поправочный член из уравнения (5), а – единичный вектор по оси

Этот второй способ нахождения гравитационной силы в расчетном отношении эффективнее, чем оценочное уравнение (37), потому что градиент потенциала является локальным параметром, который можно вычислить в той же части алгоритма гидрокода, где вычисляются плотность и другие величины. Он имеет то дополнительное преимущество, что полученная сила сглажена по процедуре интерполяции метода SPH и позволяет избежать расходимостей, когда две частицы подходят слишком близко друг к другу. На рис. 5 (внизу справа) показаны профили силы гравитации, вычисленной по уравнению (45) (закрашенные треугольники), и члена градиента давления (сплошная линия) вдоль структуры солнцеподобной политропы. Как можно увидеть, совпадение вполне удовлетворительно, за исключением поверхности, где градиент давления завышен. Хотя расчеты гравитации с использованием потенциала не так точны, как непосредственные расчеты, они в два раза быстрее, поскольку требуют меньшего количества численных операций в двойном цикле программы расчета гравитации.

Излишне говорить, что простота предложенной схемы облегчает параллелизацию расчетных модулей гравитации. В этом случае, расчеты для частиц можно будет выполнять даже на ноутбуке с многоядерным процессором.