3.2. Учет теплопроводности

Дифференциальное уравнение, описывающее эволюцию удельной внутренней энергии в результате теплопроводности:

(28)

где к – коэффициент теплопроводности, который, в свою очередь, является функцией локального термодинамического состояния вещества. Основная трудность записи уравнения (28) в виде дискретного уравнения, подходящего для расчетов по методу SPH, заключается в существовании второй производной. Хорошо известно, что производные второго и более высоких порядков влекут за собой многочисленные трудности при расчетах в неупорядоченных системах. Один из способов устранить этот дефект – это понизить порядок производной, перейдя к интегральной форме уравнения (28), Brookshaw (1985). Как было показано (см., например, Jubelgas, Springel & Dolag 2004), в трехмерных декартовых координатах следующее выражение позволяет аппроксимировать вторую производную, используя только первую производную ядра интерполяции:

(29)

где Y представляет скалярную величину, а . Полезное алгебраическое выражение, которое позволяет записать уравнение переноса тепла в формализме метода SPH, выглядит следующим образом:

. (30)

Комбинируя уравнения (29) и (30), получаем стандартную форму уравнения переноса тепла, используемую в трехмерном методе SPH. Математическое выражение для уравнения переноса тепла в осесимметричном варианте метода SPH было представлено в работе Brookshaw (2003). Однако при выводе уравнения (29) не учитывался член , который естественным образом возникает всякий раз, когда дивергенция вектора оценивается в цилиндрических координатах:

. (31)

В разделе 4.1 будет показано, как включение первого члена в правую часть уравнения (31) улучшает результаты в конкретном тестовом примере.

Чтобы получить адекватную численную аппроксимацию для уравнения (28) в осесимметричном варианте метода SPH, воспользуемся сначала уравнением (30):

(32)

Затем, используя уравнение (31) для разложения каждого члена внутри скобок и используя двухмерный оператор вместо , получаем следующее выражение:

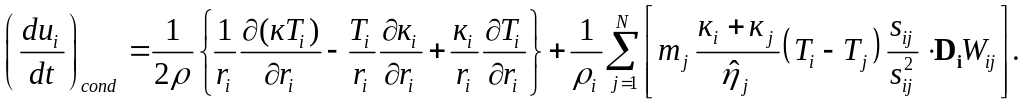(33)

Величины в скобках являются новыми членами, относящимися к окружному напряжению. Чтобы вычислить производные, воспользуемся одним из золотых правил метода SPH (Monaghan 2005):

(34)

После некоторых алгебраических преобразований получаем:

(35)

Присутствие в уравнении гарантирует отсутствие теплового потока между различными частями изотермической системы. Заметим, что присутствие множителя во втором члене в правой части уравнения (35) не гарантирует полного сохранения теплового потока. Однако суммарные потери энергии в приведенной ниже численной тестовой задаче, моделирующей тепловую волну, были пренебрежимо малы. Конечно, уравнение (35) можно привести к симметричному виду, взяв вместо среднее арифметическое , но в этом случае эволюция тепловой волны воспроизводится не так хорошо. Заметим также, что уравнение (35) согласуется со вторым принципом термодинамики, в том смысле, что тепло всегда перетекает от частиц с более высокой температурой к частицам с более низкой. Чтобы продемонстрировать это, возьмем две частицы i и j , такие, что . Второй член правой части уравнения становится отрицательным, так как скалярное произведение всегда отрицательно. Первый член правой части отрицателен при и положителен при . Поскольку тепловой поток от частицы i должен быть отрицательным, единственное затруднение может возникнуть, когда . Тем не менее, даже в этом случае тепловой поток отрицателен, если , так как знак второго члена в уравнении (35) превалирует. Таким образом, неравенство является достаточным условием для получения верного знака теплового потока между любыми двумя частицами. При это условие выполняется для большей части системы. Исключением может служить окрестность оси, где . Однако, в этом случае тепловой поток отрицателен благодаря симметрии. Поэтому мы ожидаем предсказуемого поведения вектора теплового потока, хотя нельзя исключить незначительные нарушения при плохом разрешении и сильных тепловых потоках вблизи . Гарантировать полное соответствие второму принципу гидродинамики можно, приняв поток между любыми двумя частицами, нарушающий этот принцип, равным нулю.