3. Добавление физических процессов: ударные волны, теплопроводность и гравитация

3.1. Искусственная вязкость

Как и в трехмерном пространстве, работа с ударными волнами в осесимметричном случае основывается на формализме искусственной вязкости. Тем не менее, существует широкий выбор алгоритмов искусственной вязкости, подходящих для метода SPH. Мы адаптировали стандартную процедуру Monaghan & Gingold (1983) к особенностям двухмерной осесимметричной гидродинамики. В этом подходе, искусственная вязкость приводит к росту вязкого объема и сдвигового давления, которое добавляется к обычному давлению газа только в тех областях, где частицы сталкиваются друг с другом (в понимании SPH¹). В трехмерном пространстве определена величина :

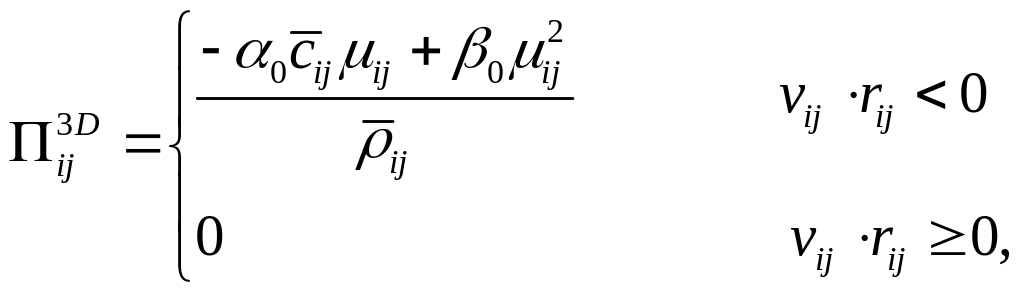(19)

которая тесно связана с вязким давлением. В уравнении (19) и являются константами порядка единицы, и – средними для плотности и скорости звука частиц i и j, а находится по формуле:

(20)

где и перестают различаться при . Скалярная величина имеет линейный и квадратичный члены. Линейная компонента имитирует объемную и сдвиговую вязкость жидкости, в то время как квадратичная компонента важна для того, чтобы избежать взаимного проникновения частиц в сильных ударных волнах.

Самый простой способ записать вклад искусственной вязкости в уравнения импульса и энергии для осесимметричного кода – это заменить массу частиц в соответствии с их удаленностью от оси Z: . Вязкое ускорение приобретает вид:

(21)

Полагая в уравнении (19), мы избавимся от явной зависимости от в формуле вязкого ускорения,

(22)

где соответствует

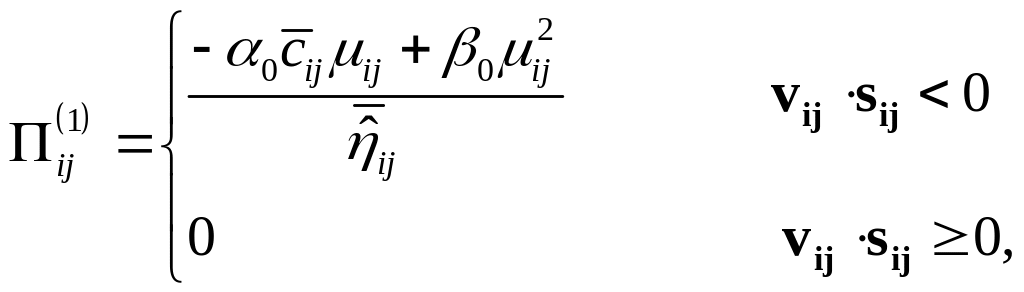(23)

причем:

(24)

Выражения (22)-(24) отвечают за декартову часть вязкости. Как было показано (см. Monaghan 2005), в непрерывном пределе эти выражения приобретают вид уравнений Навье-Стокса при условии, что коэффициенты сдвиговой и объемной вязкостей равны и соответственно. Однако, в цилиндрической геометрии, тензор напряжения, который появляется в уравнениях Навье-Стокса, также включает член, пропорциональный дивергенции скорости через посредство так называемого второго коэффициента вязкости. Поэтому в необходимо ввести дополнительный член, включающий величину , чтобы учесть схождение потока к оси. Этот новый член должен удовлетворять следующим базовым условиям. (1) Он должен быть пренебрежимо малым на достаточном расстоянии от оси, (2) должен исчезать для частиц с , (3) для случая однородного сжатия вязкое ускорение, связанное с этим членом, должно быть пренебрежимо малым, (4) он должен быть симметричным относительно частиц i и j для сохранения импульса. Выражение, удовлетворяющее всем четырем условиям:

(25)

где 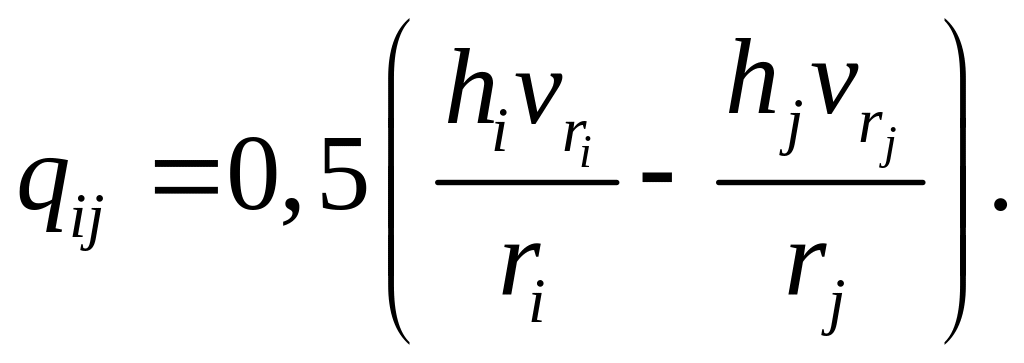Итоговая формула для вязкого ускорения выглядит следующим образом:

(26)

где Заметим, что для однородного сжатия , что означает , следовательно, градиент исчезает, и тем самым выполняется третье из выше перечисленных условий. В расходящихся ударных волнах исчезает, и остается только декартова часть вязкости. Поэтому константы должны оставаться близкими к их стандартным значениям и . Все расчеты, представленные в данной работе, были выполнены с использованием значений и . Однако, в сходящихся волнах эффект от приводит к увеличению искусственной вязкости, что вносит в систему большую диссипацию.

Уравнение (26) имеет то преимущество, что оно формально аналогично уравнению в трехмерном пространстве. Поэтому можно с удобством для себя пользоваться хорошо известными свойствами искусственной вязкости в трехмерном пространстве, которые непосредственно переносятся в осесимметричную версию (несколько полезных вариантов уравнения (19) можно найти в работе Monaghan 2005). В частности, легко записать соответствующее уравнение энергии:

(27)

которое должно быть добавлено к правой части уравнения (3).