5. Выводы

Несмотря на успех техники SPH при решении газодинамических задач в трех измерениях, на разработку двумерных (осесимметричных) приложений до настоящего момента обращали мало внимания. В данной работе была сделана попытка заполнить этот пробел, решив многие задачи, часто упоминаемые в связи с методом SPH, в цилиндрических координатах. К ним относится работа с осью сингулярности, операции с ударными и тепловыми волнами в различных астрофизических сценариях, точная процедура для нахождения гравитационной силы. Нашим основным стремлением при разработке математического формализма было оставаться как можно ближе к декартовой схеме, что позволило бы с минимальными изменениями экстраполировать многие результаты стандартного метода SPH в трех измерениях в осесимметричную версию.

Отталкиваясь от гидродинамических уравнений Эйлера, приводимых в работе Brookshaw (2003), мы получили аналитические коррекции для частиц, движущихся вблизи оси сингулярности. Эти коррекции выступают в качестве мультипликативных факторов к различным членам гидродинамических уравнений. Эти мультипликативные факторы равны единице при (рис.1), поэтому нет необходимости вычислять их вне этого диапазона, и метод оказывается выигрышным в расчетном отношении. Разработав основной формализм, мы рассмотрели несколько случаев применения нашей схемы в физике, чтобы проверить ее пригодность для решения широкого спектра задач. Прежде всего, был разработан механизм распространения трехмерной стандартной искусственной вязкости на двухмерные осесимметричные случаи, уравнения (22)-(25). Искусственная вязкость включает сходимость потока по направлению к оси симметрии посредством линейных и квадратичных членов, пропорциональных (где – расстояние до оси симметрии). Эти члены возникают из-за того, что диагональная часть тензора напряжения в цилиндрических координатах включает дивергенцию скорости потока. Однако декартова часть дивергенции уже была представлена в стандартном формализме уравнений (22) и (23), что привело к появлению объемной и сдвиговой вязкости. Поэтому была добавлена только сходящаяся часть дивергенции скорости, пропорциональная . Полученная в результате вязкая сила включает два члена: (декартова часть) и (часть, включаемая при схождении к оси), которые рассчитываются при помощи сходных выражений, уравнения (23) и (25), в состав которых входят четыре константы и Часть вязкости, стремящаяся к оси, понадобится нам только для случаев сильных имплозий. Хотя для моделей, описанных в данной работе, мы взяли и , существуют и другие комбинации, достойные изучения. Аналогичный подход был использован для построения уравнения переноса тепла. Отталкиваясь от выражения, предложенного Brookshaw (1985), мы добавили новый член, учитывающий дивергенцию температурного градиента в окрестности оси. Хотя полученное выражение и не было полностью анти-симметричным, оно привело к удовлетворительному сохранению энергии в тестах, описанных в разделах 4.1 и 4.4. Наконец, в довершение набора уравнений в него была включена самогравитация. В осесимметричной геометрии для расчета гравитации лучше рассматривать случаи прямого взаимодействия, кольцо с кольцом. Такая процедура, хотя, в целом, она и требует больших вычислительных затрат, имеет ряд преимуществ: (1) она не опирается ни на какой вид сетки и дает точное значение гравитационной силы, (2) расчеты осуществляются для умеренного числа частиц (т.е. около на серийных ноутбуках), чего зачастую оказывается достаточно для многих двумерных моделей, и (3) схема наглядна и чрезвычайно проста, что делает ее удобной для сравнений. Алгоритм, разработанный для вычисления гравитации, доказал свою пригодность в случае коллапса при свободном падении однородной сферы, а также однородного вращающегося цилиндра. При заданном характере вращения эволюция каждой точки цилиндра находится путем ввода сохранения углового момента вокруг оси симметрии.

Чтобы проверить расчетную схему, мы рассмотрели пять тестовых примеров. В каждом из них проверялось конкретное физическое явление: теплопроводность (разделы 4.1 и 4.4), ударные волны (разделы 4.3 и 4.4) и гравитация (разделы 3.3.1 и 4.2). Сохранение импульса специально проверялось в разделе 4.5. Поскольку по большей части первоначальные конфигурации имели сферическую симметрию, сохранение этой симметрии во время коллапса и дальнейшей экспансии системы рассматривалось нами, в целом, как показатель способности схемы справляться с большими изменениями пространственной шкалы. Также удалось выполнить детальное сравнение наших результатов с результатами, полученными либо из аналитических расчетов, как это было в случае распространения тепловой волны, либо при одномерном моделировании, выполненном с использованием стандартной лагранжевой гидродинамики. Сравнение показало, что наши результаты, полученные на основе нескольких десятков тысяч частиц, хорошо согласуются и с аналитическими решениями, и с одномерным моделированием. Кроме того, наблюдалось превосходное сохранение импульса, в то время как численные потери энергии никогда не превышали 1%. Сферическая симметрия сохранялась хорошо, хотя в тесте с имплозией капсулы и присутствовало легкое отклонение, частично из-за так называемой неустойчивости песочных часов (в результате первоначального размещения частиц на решетке), а частично, несмотря на коррекционные члены, – из-за действия, оказываемого на приближающиеся частицы осью сингулярности. Подобный, но, пожалуй, более трудоемкий, тест представляла собой задача о взаимодействии с преградой ударной волны (?), в которой речь шла о сферически симметричной имплозии сверхзвукового потока газа. Хотя результаты и не столь хороши, как те, что были получены при помощи других методов, не использующих искусственную вязкость, они сопоставимы с одномерными расчетами с одинаковым разрешением, основанными на схемах искусственной вязкости. Однако, результаты улучшились, когда мы подключили искусственную теплопроводность, которая определяется по уравнениям (35) и (53).

Как было сказано в разделе 4.5, слабым местом этого формализма является то, что включение отражательных частиц в схему может ухудшить сохранение полного импульса в направлении . Однако, в тех системах, в которых поле скорости не слишком анизотропно, можно ожидать сохранение импульса, гораздо лучшее, чем, к примеру, сохранение энергии. Если ожидается сильный обмен импульсами вдоль оси как это было в тесте, описанном в разделе 4,5, импульс будет сохранен в такой же степени, как полная энергия.

В заключение можно сказать, что формализм осесимметричного метода SPH, представленный в данной работе, является надежным инструментом для выполнения моделирования с использованием этого метода частиц. Однако здесь еще остается ряд нерешенных вопросов, заслуживающих дальнейшего исследования. Один из них заключается в том, как построить хорошую стартовую модель, не размещая частицы различной массы по квадратным решеткам. Это важно, так как упорядоченные решетки вызывают паразитные неустойчивости в системе, а смешение частиц с разной массой может привести к численным артефактам. Другое затруднение связано с искусственной вязкостью, поскольку она вводит слишком большую сдвиговую вязкость в систему, заглушая нормальное развитие гидродинамических неустойчивостей. Новый член вводимый уравнением (25) для искусственной вязкости, происходит от диагонали тензора напряжения, так что его вклад в сдвиговую вязкость, возможно, ниже, чем вклад В любом случае, формулировка искусственной вязкости, предлагаемая в данной работе, настолько близка к стандартной, что в будущем ее можно будет обогатить за счет достижений, сделанных в гораздо более изученном трехмерном методе SPH. Наконец, простой тест с имплозией вращающегося цилиндра показывает, что осесимметричный метод SPH способен рассчитывать вращающиеся структуры, а вот для включения переноса углового момента в численную схему потребуется больше усилий.

БЛАГОДАРНОСТИ

Авторы хотели бы поблагодарить рецензента за многочисленные поправки и предложения. В особенности, за предложение включить в статью тест Ноха и сценарий столкновения облаков, описанные в разделах 4.4 и 4.5, а также за творческий стимул к обсуждению вращения в разделе 3.3.1. Данное исследование финансировалось испанским филиалом организации DGICYT grants AYA2005-08013-C03-01, а также получило поддержку от DURSI, Generalitat de Catalunya.

ЛИТЕРАТУРА

Blondin J.M., Lundquist P. Chevalier R.A., 1996, ApJ, 472, 257

Brookshaw L., 1985, Proc. Astron. Soc. Aust., 6, 207

Brookshaw L., 2003, ANZIAM J, 44, C114

Cabezón R., García-Senz D., Relaño A., 2008, J. Comput. Phys., 227, 8523

Gingold R.A., Monaghan J.J., 1997, MNRAS, 181, 375

Herant M., Benz., W., 1992, ApJ, 387, 294

Hernquist L., Katz N., 1989, ApJS, 70, 419

Jubelgas M., Springel K., Dolag K., 2004, MNRAS, 351, 423

Lucy L. B., 1977, AJ, 82, 1013

Monaghan J. J., 1989, J. Comput. Phys., 82, 1

Monaghan J. J., 1992, Annu. Rev. Astron. Asrophys., 30, 543

Monaghan J. J., 2005, Rep. Prog. Phys., 68, 1703

Monaghan J. J., Gingold R. A., 1983, J. Comput. Phys., 52, 374

Noh W. F., 1987, J. Comput. Phys., 72, 78

Omang M., Borve S., Trulsen J., 2006, J. Comput. Phys., 213, 391

Omang M., Borve S., Trulsen J., 2007, Shock Waves, 16, 467

Owen J. M., Villumsen J. V., Saphiro P. R., Martel H., 1998, ApJS, 116, 155

Petscheck A. G., Libersky L. D., 1993, J. Comput. Phys., 109, 76

Velarde P., García-Senz D., Bravo E., Ogando P., Relaño A., García C., Oliva E., 2006, Phys. Plasmas, 13, 092901

ПРИЛОЖЕНИЕ А: КОРРЕКЦИОННЫЕ МНОЖИТЕЛИ ВБЛИЗИ ОСИ

Прежде всего, выведем множитель влияющий на двухмерную плотность Из-за симметрии относительно оси трехмерная плотность должна иметь вблизи оси максимум или минимум. Таким образом, мы можем положить в окрестности оси Если сделать одномерную оценку средней плотности вдоль оси по методу SPH,

(А1)

где – ядро кубического сплайна в одном измерении:

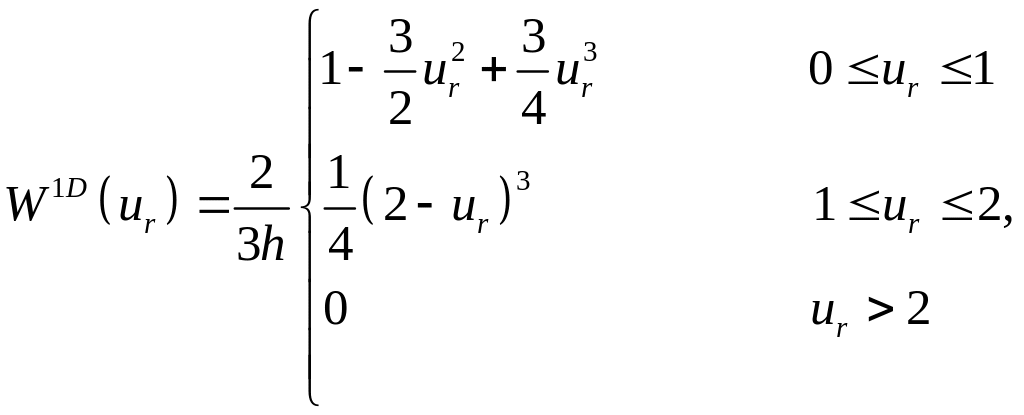(А2)

причем Если взять что выполняется только при то

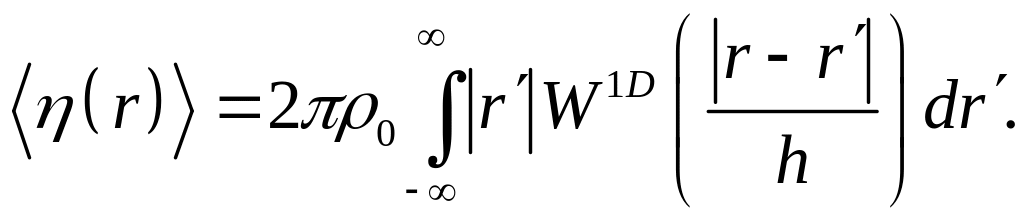(А3)

Используя кубический сплайн можно проинтегрировать правую часть уравнения А3, в результате получаем:

(А4)

где и – это скорректированная плотность (здесь и далее все скорректированные величины отмечены крышечкой). Коррекционный множитель дан в уравнении (5). Плотность в угловых скобках – это величина, найденная по методу SPH с использованием сумм вместо интегралов. Таким образом, добавляя координату по оси и используя можно оценить скорректированную плотность по формуле:

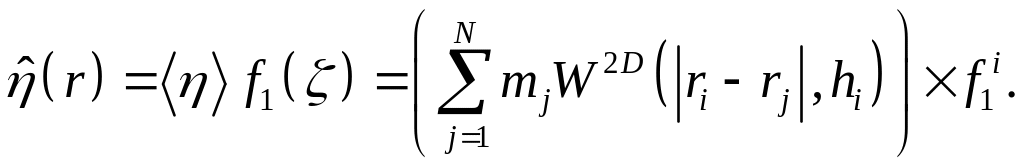(А5)

Аналогичным приемом можно воспользоваться для получения адекватных выражений для и , которые нужны для расчета временной эволюции плотности, см. уравнение (15). Из-за симметрии радиальная скорость около оси симметрии обращается в ноль, поэтому вблизи оси и

(А6)

Снова интеграл в правой части допускает аналитическое решение для ядра кубического сплайна. После некоторых алгебраических преобразований получаем:

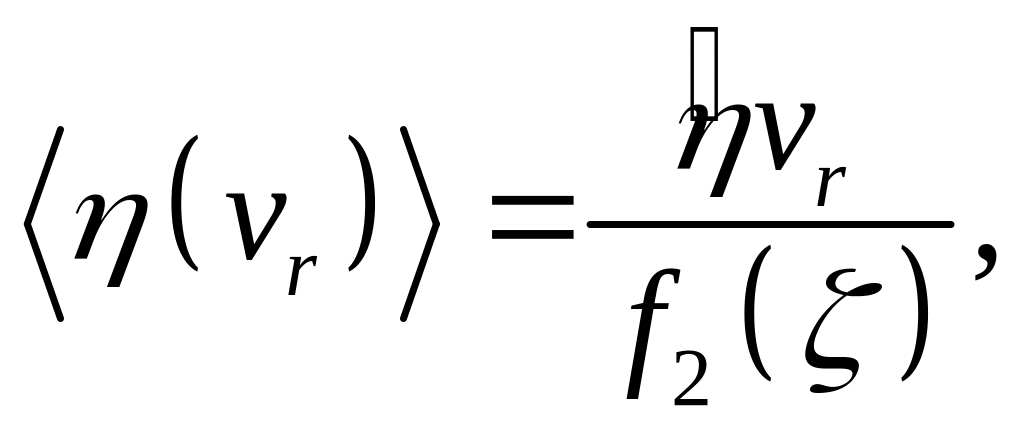(А7)

где находится из уравнения (16). Выражение в угловых скобках – это то, что выдает численных код при использовании сумм вместо интегралов. Таким образом, скорректированная величина равна:

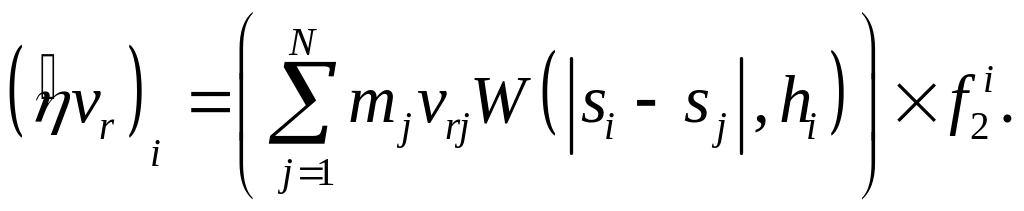(А8)

Подобным образом скорректируем

(А9)

и соответствующее дискретное выражение:

(А10)

Графики множителей и а также их радиальных производных приведены на рис. 1. Множитель в точности равен единице при и сводится к нулю, когда , как и ожидалось. Однако, множитель , как можно заметить, близок, но не равен единице при и имеет не такой пологий наклон. Это объясняется тем, что интегральное выражение в уравнении (А6) является квадратичным по радиальной координате , из-за чего интерполяция не дает точного значения