4.4. Ударная волна нагрева стенки

Тест ударной волны нагрева стенки, разработанный Нохом (Noh) в 1987 году, предназначался специально для анализа поведения алгоритмов, созданных, чтобы отслеживать сильные ударные волны. В основе своей тест ударных волн нагрева стенки заключается в том, чтобы «взорвать внутрь» сферу или цилиндр, навязав им сходящееся поле скоростей. Для таких геометрий существует аналитический подход к эволюции плотности и термодинамически переменных как функций начальных условий. Результаты численных рассчетов можно сравнить с аналитическим решением, чтобы найти наилучший метод или выбрать оптимальную комбинацию параметров. Хорошо известно, что схемы, опирающиеся на искусственную вязкость, испытывают трудности при работе с тестом ударной волны нагрева стенки. Причиной является то, что искусственная вязкость распространяет ударную волну на три или четыре расчетные ячейки, что вызывает неестественный рост внутренней энергии перед ударной волной. В случае сферической или цилиндрической геометрии искусственное увеличение внутренней энергии усиливается геометрическим схождением ударной волны. Таким образом, задача ударной волны стенки выдвигает высокие требования к осесимметричному методу SPH. Brookshaw (2003) выполнил аналогичный тест при помощи кода SPH, но далеко от оси симметрии. В частности, он смоделировал столкновение двух сверхзвуковых потоков газа, получив хорошие профили для плотности и внутренней энергии для всех точек, за исключением небольшой области у оси столкновения. На профиле плотности в этой области виден спад, в то время, как внутренняя энергия демонстрирует резкий подъем. И спад, и подъем являлись численными артефактами, которые можно было бы сгладить, используя член искусственной теплопроводности для размазывания излишка внутренней энергии и уменьшения погрешности вблизи контактного разрыва.

Чтобы проверить эффективность нашего кода, мы разместили частиц на квадратной решетке. Как и в предыдущих тестах, масса частиц была сформирована таким образом, чтобы воспроизвести сферическую однородную систему с начальным радиусом Начальные условия были взяты такими же, как в работе Ноха (1987): Точное решение в момент времени для показано на рис.8 (пунктирная линия). Аналитический профиль характеризуется постоянным послеударным состоянием вплоть до расстояния , после чего наступает резкое уменьшение плотности и внутренней энергии. В зоне ударной волны плотность достигла постоянного значения в то время как внутренняя энергия была Комбинация таких жестких начальных условий с геометрической сходимостью приводит к сильной имплозии, жестче даже чем та, которая была описана в примере с капсулой.

На рис. 8 (слева) показаны сферически усредненные профили плотности и внутренней энергии, полученные с использованием метода SPH, при Величины ошибок на графике дают дисперсию этих переменных по отношению к среднему значению в ячейке. Как можно увидеть, итоговые профили плохо согласуются с аналитическими результатами в зоне столкновения. Кроме того, наблюдается большая дисперсия, особенно при малых радиусах, – явный признак численного шума. Вблизи оси имеется типичная искусственная комбинация провала (плотности) и пика (внутренней энергии). Максимальное значение плотности составило , что примерно на 10% ниже точного значения. Такое плохое количественное совпадение не было для нас неожиданностью, так как оно является общим для всех гидрокодов, использующих схему искусственной вязкости. Один из способов улучшить качество моделирования заключается в том, чтобы сделать поправку на теплопроводность в гидрокоде, которая устранит пик тепловой энергии и отчетливее выделит ударную волну.

о

радиус

о

радиус

о

радиус

о

радиус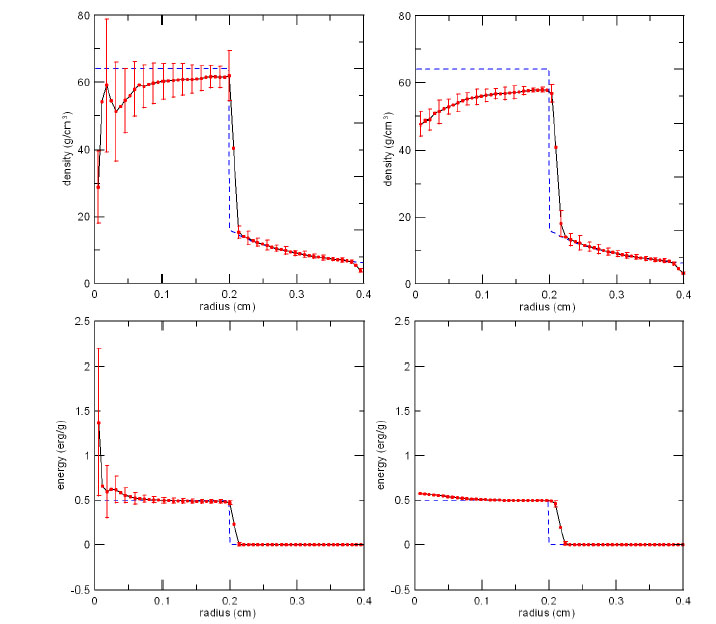

Рис. 8. Результаты теста Ноха при Верхний ряд: профили средней плотности с искусственной теплопроводностью (справа) и без нее (слева). Нижний ряд: то же самое для внутренней энергии. Дисперсия вокруг средних значений дана в виде отрезков, показывающих границы погрешности.

Рекомендации по получению коэффициента искусственной теплопроводности в методе SPH для более успешного решения задачи о взаимодействии с преградой ударной волны были представлены в работах Monaghan (1992) и Brookshaw (2003). Для этого расчета мы воспользовались методом Monaghan применительно к характеристикам осесимметричного метода SPH, определяющим искусственную теплопроводность для i-частицы

(53)

где – симметризованная удельная теплоемкость, а – параметр искусственной вязкости, получаемый из уравнения (24). Согласно уравнению (53), , что можно использовать непосредственно в уравнении (35) для вычисления искусственного теплового потока. Как показано на рис. 8 (справа), включение члена искусственной теплопроводности приводит к значительному улучшению результатов. Не только был ликвидирован глубокий провал плотности в центральной области, но и существенным образом уменьшилась дисперсия вокруг средних значений для плотности и внутренней энергии. Однако пик максимальной плотности по-прежнему остается на 10% ниже теоретического значения. В этом отношении, единственный способ улучшить результаты – это отчетливее выделять ударную волну, используя адаптивные ядра, как это делают Owen et al. (1998), Cabezón, García-Senz&Relaño (2008), или увеличивая количество частиц.