Лабораторная 6. Решение дифференциальных уравнений в MathCad

Цель работы:

• Освоить приемы, средства и методы решения дифференциальных уравнений в MathCad;

• Научиться пользоваться и применять команды меню, встроенные функции для решения дифференциальных уравнений в MathCad;

• Составлять программный код и использовать численные методы для решения дифференциальных уравнений в MathCad.

Задания:

1. Освоить работу и параметры функций в MathCad для решения дифференциальных уравнений;

2. Освоить работу и параметры функций в MathCad для решения систем дифференциальных уравнений;

3. Составить программу для решения дифференциальных уравнений (систем дифференциальных уравнений) первого порядка;

4. Решение ОДУ в заданной точке;

5. Решение систем ОДУ высших порядков;

6. Составить программный код и алгоритм для решения; дифференциальных уравнений в частных производных;

7. Составить программу для решения систем дифференциальных уравнений в частных производных (уравнение теплопроводности).

Выполнение одного варианта задания

1. Численное решение осуществляется при помощи встроенной функции rkfixed(y,x1,x2,n,D), которая использует метод Рунге-Кутта 4-го порядка.

y - вектор начальных условий, в данном случае вектор из одного элемента.

x1,x2 - границы интервала для поиска решения.

n - количество точек на интервале.

D(x,y) - вектор-функция первых производных, в данном случае вектор из одного элемента.

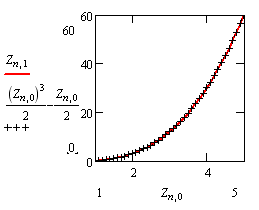
Решение уравнения на интервале (1..5). Матрица Z имеет 2 столбца и 40 строк.

Первый столбец содержит х переменную, второй - y.

3. Системы линейных уравнений первого порядка. Решаются с помощью этой же функции. Решим для примера систему 2-х дифференциальных уравнений 1-го порядка.

4.,5. Дифференциальное уравнение 2-го порядка. Решается аналогично, путём сведения уравнения 2-го порядка к системе 2-х уравнений 1-го порядка, например, решим уравнение:

6.,7 Дифференциальные уравнения в частных производных представляют собой одну из наиболее сложных и одновременно интересных задач вычислительной математики. Эти уравнения характеризуются тем, что для их решения не существует единого универсального алгоритма и большинство задач требует своего собственного особого подхода. Уравнениями в частных производных описывается множество разнообразных физических явлений, и с их помощью можно с успехом моделировать самые сложные явления и процессы (диффузия, гидродинамика, квантовая механика, экология и т. д.). Дифференциальные уравнения в частных производных требуют нахождения функции не одной, как для ОДУ, а нескольких переменных, например f(x,y) или f(x,t). Постановка задач включает в себя само уравнение (или систему уравнений), содержащее производные неизвестной функции по различным переменным (частные производные), а также определенное количество краевых условий на границах расчетной области.

Несмотря на то, что Mathcad обладает довольно ограниченными возможностями по отношению к уравнениям в частных производных, в нем имеется несколько встроенных функций, количество и возможности которых увеличились в новой 11-й версии. Решать уравнения в частных производных можно и путем непосредственного программирования пользовательских алгоритмов

Классификация уравнений в частных производных

Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяется спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например u<x,t) в некоторой области определения аргументов 0< х < L и 0< t < T. Граничные условия определяются как заданные временные зависимости функции и, или производных этой функции на границах расчетной области 0 и L, а начальные - как заданная u(х, 0).

Сами уравнения в частных производных (несколько условно) можно разделить на три основных типа:

• параболические — содержащие первую производную по одной переменной и вторую — по другой, причем все эти производные входят в уравнение с одинаковым знаком;

• гиперболические — содержащие первую производную по одной переменной и вторую — по другой, входящие в уравнение с разными знаками;

• эллиптические — содержащие только вторые производные, причем одного знака.

Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений.

Контрольные вопросы

1. Какие уравнения называются дифференциальными?

2. Какие функции MathCad реализует решение дифференциальных уравнений методом Рунге-Кутта?

3. В каких случаях целесообразно применять адаптируемый метод Рунге-Кутта?

4. Какие функции применяются для решения дифференциальных уравнений Пуассона и Лапласа?

5. Что такое жесткие системы дифференциальных уравнений и какие функции применяются для их решения?

6. Какие функции применяются для решения дифференциальных уравнений в частных производных?