Лабораторная 4. Обработка данных и статистика в MathCad

Цель работы:

• Освоить приемы и средства обработки данных;

• Научиться пользоваться и применять различные статистические функции при анализе данных и получения графиков;

• Знать основные численные методы, используемые в MathCad для проведения статистического анализа.

Задания:

1. По заданным в виде векторов, или электронных таблиц испытательным данным и используя встроенные функции выполнить одномерную сплайн-интерполяцию и аппроксимацию;

2. С помощью статистических функций рассчитать среднее значение элементов вектора, дисперсию для элементов вектора, среднеквадратическую погрешность (квадратный корень из дисперсии), стандартное отклонение элементов вектора, вектор частот попадания данных в заданные интервалы;

3. Выполнить линейную регрессию для совокупности данных с использованием ряда функций;

4. Выполнить линейную регрессию общего вида для совокупности данных с использованием ряда функций;

5. Выполнить нелинейную регрессию общего вида с использованием ряда функций;

6. Выполнить экспоненциальную и синусоидальную регрессию для совокупности данных с использованием ряда функций;

7. Используя статистические функции MathCad, осуществить сглаживание данных;

8. Выполнить предсказание (экстраполяцию) по некоторой совокупности данных.

Выполнение одного варианта задания

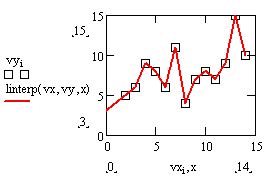
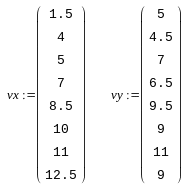
1. Линейная интерполяция. Функция linterp(vx,vy,x).

vx, vy - векторы данных, причём данные должны быть упорядочены по возрастанию.

x - аргумент, для которого возвращается значение y.

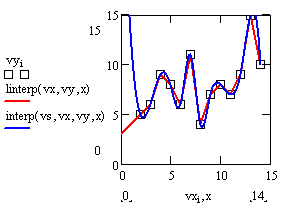
Кубическая сплайн-интерполяция позволяет провести через набор точек гладкую кривую так, чтобы в этих точках были непрерывны первая и вторая производные. Интерполяция осуществляется двумя функциями. Вначале вычисляется вектор вторых производных в рассматриваемых точках vs:=cspline(vx,vy), затем вычисляется значение функции в точке x interp(vs,vx,vy,x).

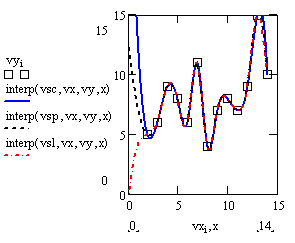
Попробуем интерполировать рассмотренный набор точек с использованием трёх различных вариантов кубической интерполяции.

2. В MathCAD 2001 имеется ряд встроенных функций для расчетов числовыхстатистических характеристик рядов случайных данных. - mean(x) - выборочное среднее значение; - median (х") - выборочная медиана (median) - значение аргумента, которое делит гистограмму плотности вероятностей на две равные части; - var(x) - выборочная дисперсия (variance); - stdev(x) - среднеквадратичное (или "стандартное") отклонение (standard deviation); - max(x), min(x) - максимальное и минимальное значения выборки; - mode(x) - наиболее часто встречающееся значение выборки; - Var (x), stdev(x) - выборочная дисперсия и среднеквадратичное отклонение в другой нормировке;

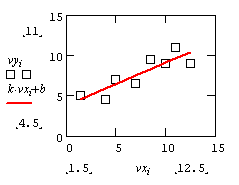
3. В отличие от интерполяции, регрессия не требует, чтобы кривая непременно проходила через все точки. Напротив, задача ставится так: построить кривую, наиболее близко, в смысле минимального среднеквадратичного отклонения, описывающую данный набор точек.

Для точек данных, из предыдущего занятия, необходимо построить прямую y=kx+b, сумма квадратов отклонений всех точек от которой будет минимальной.

Параметры этой прямой возвращают две встроенные функции Mathcad:

k=slope(vx,vy) - угловой коэффициент, b=intercept(vx,vy) - свободный член.

4. Для построения полинома n-го порядка, описывающего данный набор точек, используется функция интерполяции interp(vs,vx,vy,x), где vs - вектор вторых производных вычисляется при помощи функций regress(vx,vy,n) или loess(vx,vy,span). Отличие последних функций заключается в том, что первая из них строит полином n-го порядка, а вторая, строит несколько таких полиномов, их количество определяется величиной последнего параметра span.

5.,6. Описать зависимость в виде линейной комбинации произвольных функций, например, в виде комбинации синусов и косинусов, как в разложении Фурье, или какого-то другого набора функций.

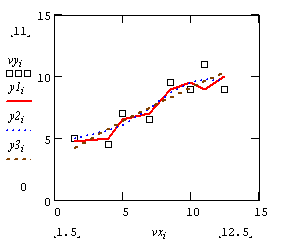
7. Сглаживание предполагает использование набора значений y и возвращение нового набора y, который является более гладким, чем исходный набор. Имеется набор из 3-х функций, реализующих различный алгоритм сглаживания:

medsmooth(vy,n) - метод скользящей медианы,

ksmooth(vx,vy,b) - метод Гаусса,

supsmooth(vx,vy) - метод наименьших квадратов.

Все эти функции возвращают новый набор значений функции. n - ширина окна сглаживания, b - параметр сглаживания (должен быть больше интервала между точками).

8. В Mathcad есть функция predict(v,m,n), которая позволяет сделать предсказание поведения функции вне интервала её задания. Эта функция использует линейный алгоритм предсказания. Здесь v - вектор данных, m - количество последовательных точек исходного вектора используемых для предсказания (все точки заданны с равным шагом), n - количество предсказываемых точек.

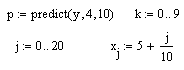
Контрольные вопросы:

1. Какие функции MathCad способны осуществить сплайн-интерполяцию, аппроксимацию и чем они отличаются?

2. С помощью каких статистических функций можно рассчитать в MathCad статистические показатели?

3. Чем отличается линейная регрессия от линейной регрессии общего вида?

4. Какие параметры и какого типа входят в функцию для проведения нелинейной регрессии общего вида?

5. Какие функции способны осуществить сглаживание данных?

6. Что из себя представляет и какими функциями осуществляется предсказание?