47

Математический анализ

§ 1. Логическая символика, множества и операции над ними

Определение 1. Пустым называется множество, которое не содержит ни одного элемента.

Пусть даны два множества и .

Определение 2. Объединением двух множеств и называется множество, которое состоит из тех и только тех элементов, которые принадлежат хотя бы одному из множеств и :

.

Определение 3. Пересечением двух множеств и называется множество, состоящее из тех и только тех элементов, которые принадлежат как множеству , так и множеству :

.

Если , то говорят, что множества и не пересекаются.

Определение 4. Если каждый элемент множества является одновременно и элементом множества , то множество называется подмножеством множества :

.

Определение 5. Пусть множество является подмножеством множества . Тогда дополнением множества на множество называется множество, которое состоит из тех и только тех элементов, которые принадлежат множеству , но не принадлежат множеству .

Множество называется конечным, если оно содержит конечное число элементов. В противном случае его называют бесконечным.

§ 2. Функции и их классификация

Рассмотрим два множества и .

Определение. Соответствие, при котором каждому элементу из множества сопоставляется единственный элемент из множества , называется функцией . При этом имеется в виду, что для любого элемента ( ) существует элемент ( ) такой, что .

Множество называется областью определения, а множество – областью значений функции .

Существуют различные способы задания функций:

1. с помощью диаграмм:

2. с помощью таблиц:

3. а

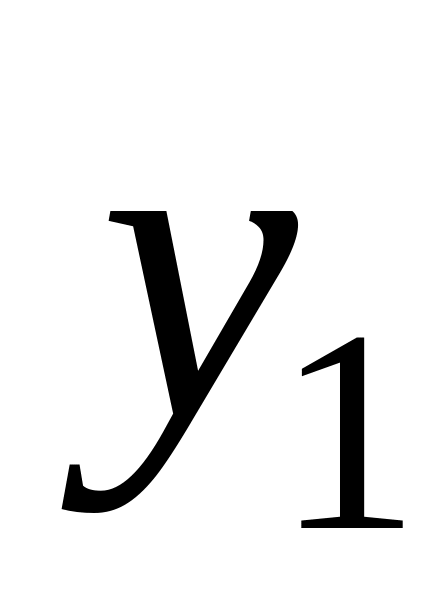
   налитический (с помощью формулы):

.

Если к формуле не дописываются дополнительные условия, то областью определения функции, задаваемой этой формулой, считается множество всех значений переменной , при которых эта формула имеет смысл.

Пример.

а) ( ).

.

б) .

.

4. графический:

1. Четность и нечетность функции

Функция называется четной, если для любых и , принадлежащих множеству , выполняется: .

График четной функции симметричен относительно оси ординат.

Функция называется нечетной, если для любых и , принадлежащих множеству , выполняется: .

График нечетной функции центрально симметричен относительно начала координат.

2) Промежутки возрастания и убывания функции (монотонность).

Функция называется возрастающей на рассматриваемом промежутке, если большему значению аргумента соответствует большее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х₁ и х₂, причём х₁ > х₂, то у(х₁) > у(х₂).

Функция называется убывающей на рассматриваемом промежутке, если большему значению аргумента соответствует меньшее значение функции у(х). Это означает, что если из рассматриваемого промежутка взяты два произвольных аргумента х₁ и х₂, причём х₁ < х₂, то у(х₁) < у(х₂).

3) Нули функции.

Точки, в которых функция F = y (x) пересекает ось абсцисс (они получаются, если решить уравнение у(х) = 0) и называются нулями функции.

4) Периодичность функции.

Функция называется периодической, если существует такое число , что для любого выполняется соотношение: , при этом наименьшее положительное из всех таких чисел называется периодом функции.

5) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.