ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции. Интегральное исчисление решает обратную задачу — нахождение самой функции по ее производной или дифференциалу.

НЕОПРДЕЛЕННЫЙ ИНТЕГРАЛ

1. Первообразная функция и

неопределенный интеграл

Определение. Функция называется первообразной функцией для функции на промежутке , если в каждой точке этого промежутка .

Например, является первообразной для функции ,так как .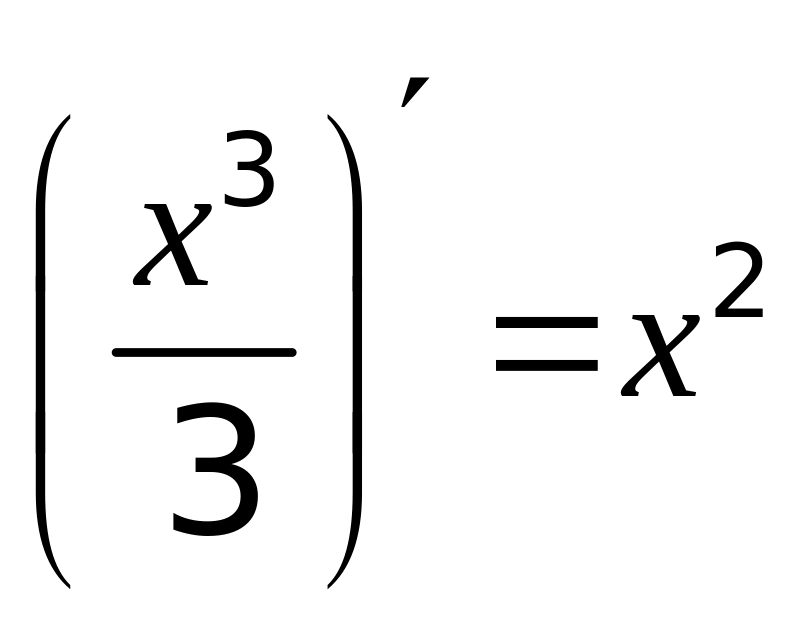

Следует отметить, что для заданной функции ее первообразная определена неоднозначно. Дифференцируя, нетрудно убедиться, что функции - , и вообще , где — некоторое число, являются первообразными для функции . Аналогично, в общем случае, если — некоторая первообразная для , то, поскольку , функции вида , где — произвольное число, также являются первообразными для ‚(х).

Остается вопрос, описывает ли выражение вида все первообразные для функции . Ответ на него дает следующая теорема.

Теорема. Если и — первообразные для функции в некотором промежутке , то найдется такое число , что справедливо равенство

.

Доказательство. Поскольку

,

то, по следствию из теоремы Лагранжа, найдется такое число , что или .

Из данной теоремы следует, что, если — первообразная для функции , то выражение вида , где — произвольное число, задает все возможные первообразные для .

Определение. Совокупность всех первообразных для функции на промежутке Х называется неопределенным интегралом от функции и обозначается , где – знак интеграла, – подынтегральная функция, – подынтегральное выражение.

Таким образом,

(10.1)

где — некоторая первообразная для , — произвольная постоянная.

Например, поскольку — первообразная для функции ,то

.

Отметим, что в определении неопределенного интеграла не исключается, что сама возможно является функцией некоторой переменной, однако при проверке правильности нахождения первообразной это несущественно, так как дифференцировать следует лишь по переменной (по переменной, стоящей в формуле (10.1) под знаком дифференциала).

Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.

В гл. 11 будет показано, что достаточным условием интегрируемости функции на промежутке является непрерывность функции на этом промежутке. (Заметим, что для дифференцируемости функции ее непрерывность является лишь необходимым, но недостаточным условием).

2. Свойства неопределенного интеграла. Интегралы от основных элементарных функций

Рассмотрим основные свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.

.

Доказательство. Дифференцируя левую и правую части равенства (10.1), получаем:

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

(10.2)

Доказательство. По определению дифференциала и свойству 1 имеем

.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

(10.3)

где — произвольное число.

Сравнивая между собой свойства 2 и З, можно сказать, что операция нахождения неопределенного интеграла и дифференциала взаимнообратны (знаки и взаимно уничтожают друг друга, в случае свойства 3, правда, с точностью до постоянного слагаемого).

4. Постоянный множитель можно выносить за знак интеграла,

т.е.

(10.4)

где — некоторое число.

Доказательство. Найдем производную функции :

(см. свойство 1). По следствию из теоремы Лагранжа найдется такое число , что и значит . Так как сам неопределенный интеграл находится с точностью до постоянного слагаемого, то в окончательной записи свойства 4 постоянную можно опустить.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.

(10.5)

Доказательство аналогично свойству 4.

Нетрудно видеть, что свойство 5 остается справедливым для любого конечного числа слагаемых.

Перечислим интегралы от элементарных функций, которые в дальнейшем мы будем называть табличными:

,

(10.6)

(10.7)

,

(10.8)

для произвольного интервала, не содержащего точки ,

,

(10.9)

,

( )

,

(10.12)

,

(10.13)

,

(10.14)

.

(10.15)

Справедливость приведенных формул проверяется непосредственно дифференцированием (см. определение неопределенного интеграла)

Пример 1. Найти интегралы:

а) ; б) ; в) .

Решение. Во всех трех случаях нам придется воспользоваться одним и тем же табличным интегралом (10.7) от степенной функции, но при разных значениях .

а) При : .

б) При : .

в) При : .

Пример 2. Найти интегралы:

а) ; б) .

Решение. а) Так как то, используя (10.4) и (10.9) при , получаем

.

в) Поскольку , то воспользуемся (10.4) и (10.14) при :

.

Метод интегрирования, основанный на применении свойств 4 и 5, называется методом разложения.

Пример 3. Используя метод разложения, найти интеграл:

.

Решение. Нахождение данного интеграла начинается с преобразования подынтегральной функции. Воспользуемся соответствующей формулой сокращенного умножения и последующим почленным делением числителя на знаменатель:

(см. табличные интегралы (10.7) и (10.8)). Обращаем внимание на то, что в конце решения записываем одну общую постоянную , не выписывая постоянных от интегрирования отдельных слагаемых. В дальнейшем мы будем опускать при записи постоянные от интегрирования отдельных слагаемых до тех пор, пока выражение содержит хотя бы один неопределенный интеграл. В окончательном ответе тогда будет одна постоянная.