10. Истечение и дросселирование газов и паров. Скорость движения потока в выходном сечении. Критическая скорость потока. Температура инверсии. Сопло Лаваля.
Дросселирование – это понижение давления вещества находящегося в потоке, вызванное гидравлическим сопротивлением канала, т.е. в процессе дросселирования давление падает без совершения работы.
если при этом теплообмен вещества с окружающей средой не происходит, такое дросселирование называется адиабатным.
величина падения давления при дросселировании зависит от природы рабочего тела, величины сужения трубопровода и скорости движения газа или пара.
Схематически процесс дросселирования изображается преодалением потока вещества какого либо сопротивления или как правило отверстия
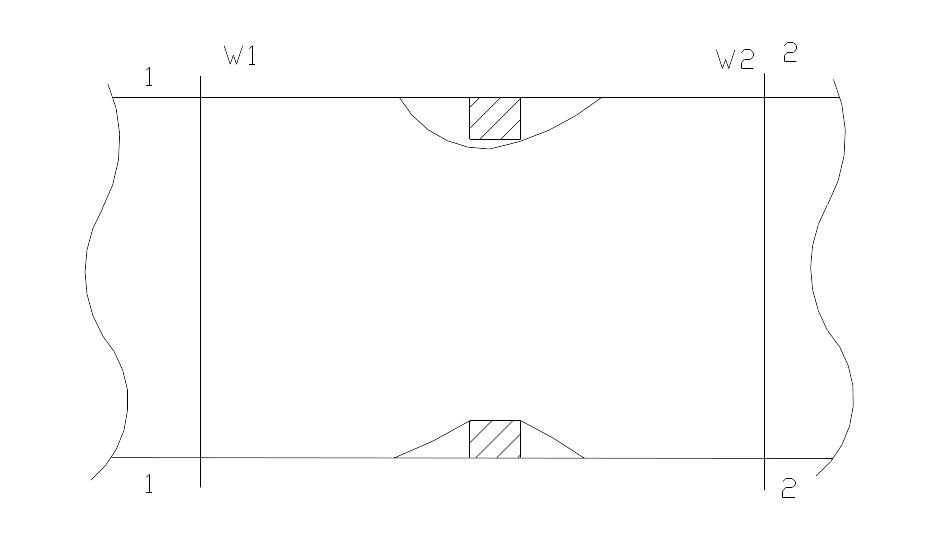
Сечение 1-1 и 2-2 достаточно удалены друг от друга, таким образом, что
ω1=ω2, но Р2<Р1
физически падение давления объясняется диссимацией, энергией потока расходуемой на преодаление местного сопротивления.
q=Δi+l` l`=0 q=0 Δi=0 или i1=i2
При дросселировании идеальных газов и жидкостей равенство энтальпий означает неизменность температуры после дросселирования. Для реальных газов и паров характерно t2<t1. т.е. в процессе дросселирования газы и пары охлаждаются.
Дросселирование водяного пара.
1-2`- пр-с уменьшения энтальпии в дросселе при падении давл-я от Р1 до Р2
2`-2- пр-с торможения потока за дросселем в рез-те кот-го кинетич. энергия уменьшается, а энтальпия возрастает до первонач. значения (теплота выделившаяся при торможении потока усваивается раб. телом).
Истечение газов и паров
q1-2=i2-i1 + (ω22 - ω21)/2 + Lотв -1ый з-н термодинамики для пр-сов истечения
если поток не производит работу и эта работа не подводится к нему dLотв=0.
При рассмотрении процессов истечения вводится след:
Пр-с истечения происходит адиабатно, т.е. отсутствует теплообмен м/у стенкой канала и средой нах-ся вокруг канала.
Пр-с стационарный это значит, что по длине канала все параметры P, t, i, S. Меняются однако в каждом сечении канала все параметры газа и скорость его течения по времени остается постоянными.
стационарный процесс подчиняется уравнению неразрывности G·υ=F·ω
G- массовый расход газа в рассматр. сечении. кг/с
υ- удельный объем газа м3/кг
ω- скорость течения в рассматр. сечении м/с
F- площадь поперечного сечения канала.
для адиабатного течения dq=0 (ω22 - ω21)/2= i1-i2 т.е. изменение внешн. кинетич. энергии рабочего тела происходит за счет уменьшения его энтальпии.
Если принять на входе в канал ω1→0, тогда скорость на входе ω2=√(2·(i1-i2))
Значение энтальпии i1 и i2 определяется по i-S диаграмме или таблице для данного вещества.
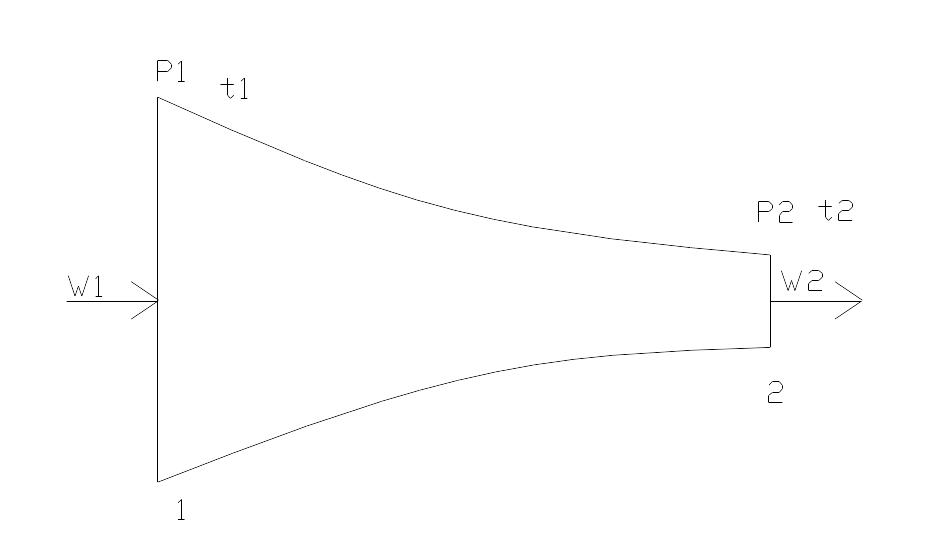
Канал в котором происходит ускорение потока, т.е. dω>0, т.е превращение потенциальной энергии в кинетическую называется соплом или конфузором.
Канал в котором происходит уменьшение сорости потока dω<0, называется диффузором.
Техническая работа процесса истечения равна только приращению кинетич. энергии газа. Lтех =(ω22 - ω21)/2
Для адиабатного процесса
Lтех =P1V1 · K/(K-1) · [1- (P2/P1)(K-1)/K ]
K=Cp/Cv - показатель адиабаты.
Учитывая, что ω1→0 приравниваем оба выражения для получения работы и получаем
ω2 = √[ P1V1 · 2K/(K-1) · [1- (P2/P1)(K-1)/K ]]
Секундный расход газа из уравнения неразрывности можно определить по формуле
G=F2· ω2/V2= F1· ω1/V1
V2 – определим с помощью уравнения адиабаты.
P1V1К = P2V2К → 1/V2 =( P2/ P1)1/К · 1/V1 ; G=F2· ω2/V1 · (Р2/Р1)1/к
из уравнения следует что F2= const секундный расход газа G зависит от физических свойств газа его начальных параметров P1,V1 и давления P2 на выходе из сопла.
Давление P2 при котором достигается максимальный расход называется критическим.
Р2кр = βкр · Р1 βкр = (2/(К+1))К/(К+1) для воздуха К=1,4; для перегретого пара К=1,3
критическое давление Р2 есть наименьшее давление которое устанавливается на выходе из сужающегося канала сопла.
При βкр<P2/P1<1 результаты опыта полностью совпадают с результатами полученными по уравнению.
В интервале 0<P2/P1< βкр теория и данные опыта расходятся. Действительный массовый расход достигнет максимума, останется постоянным. Это явление получило название кризис истечения несоответствия.
Объяснение несоответствия: при расширении газа в суживающихся соплах невозможно получить давление газа на выходе ниже некоторого критического давления соответствующего максимальному расходу газа через сопло, следовательно при сколь угодно низком давлении окружающей среды за соплом давление газа в выходном сечении суживающегося сопла остается постоянным и = Ркр, следовательно в таких соплах нельзя получить скорости на выходе ω2 больше чем критическая скорость. соответствующая критическому Ркр.
При Р2>Ркр давление газов в выходном сечении сопла равно давлению окружающей среды, в кот. истекает газ из сопла.
При Р2<Ркр давлении газа в выходном сечении сопла остается постоянным и = Ркр.
Скорость газа кот. устанавливается в выходном сечении суживающегося канала при истечении газа в окружающую среду с давлением равным или ниже критического называется критической скоростью.
ω2КР = √2Ркр · Vкр = а
а – скорость звука в газе выходном сечении сопла (343 м/с)
именно равенство ωкр=а и объясняется несоответствием опытных и теоретических данных, как только скорость потока на выходе из сопла становится равной местной скорости звука уменьшение давления окружающей среды за соплом никак не влияет на изменение скорости ω2 и расхода через сопло. они остаются постоянными.
Сопло Лаваля
Перейти через звуковую скорость удалось Шведу Лавалю, он предложил комбинированное сопло состоящее из двух частей : суживающейся и расширяющейся.
Ур-ие профиля канала dF/F = (M2 - 1) · (dω/ω)
M= ω/a
В сопле Лаваля для ускорения потока используют весь перепад давлений от Р1 до Р2.