4, Цикл и схема парокомпрессионной холодильной установки.

Схема:

1- дроссельный вентиль 2- испаритель

3- компрессор 4- конденсатор

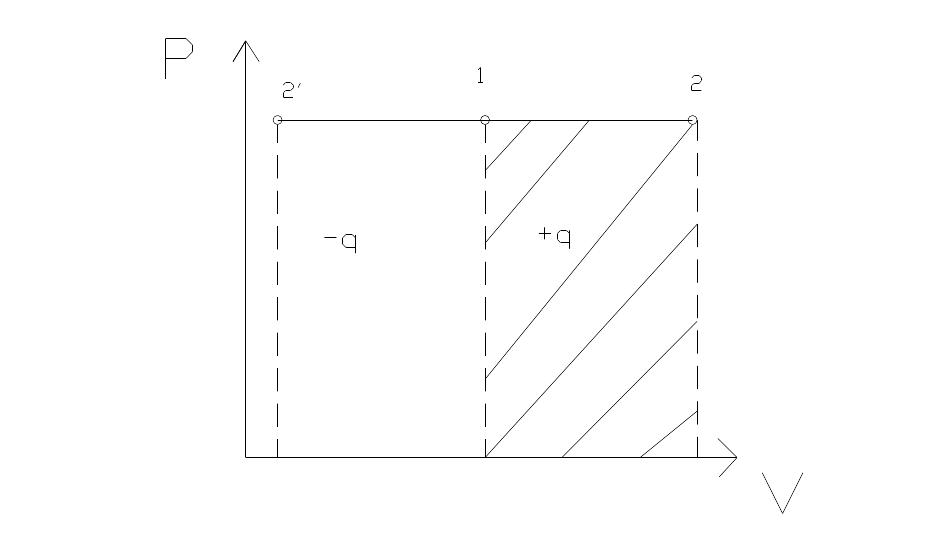
Жидкость с низкой температурой кипения (фреон 12 (-29 °С)) при P1 и T1 направляется в дроссельный вентиль 1, где она дросселируется до давления P2. При выходе из вентиля влажный пар направляется испаритель 2, где жидкость испаряется за счет тепла, отбираемого от охлаждаемых тел. Далее в компрессоре 3 пар высокой степени сухости адиабатно сжимается до P1. Затем пар направляется в конденсатор

Цикл:

1-2- расширение при дросселировании жидкости

2-3- изобарно- изотермический подвод теплоты и хладоагента в испаритель от охлаждаемого объема

3-4- адиабатное сжатие сухого пара в компрессоре

4-1- конденсация пара

5. Схема и цикл теплового насоса.

ТН- устройства предназначенные для эффективного преобразования низкой тепловой энергии природной среды и сбросной t производственной и бытовой деятельности людей на температурный уровень систем отопления и ГВС.

Схема ТН:

1. испаритель

компрессор

2. Конденсатор

3. дроссельный клапан

4. низкотемпературный источник (НИТ)

5. в систему отопления

В испаритель поступает НИТ. За счет тепла охлаждения этой воды или воздуха в испарителе происходит процесс парообразования фреонов, пары которого затем поступают в компрессор, где происходит его сжатие и повышение t, затем сжатые пары фреонов конденсируются в конденсаторе, отдавая тепло воде системы отопления или ГВС. Цикл ТН завершается дросселированием фреонов и возвратом его в ГВС.

Коэффициент преобразования- это соотношение полученной потребителем тепловой энергии (Q) к затраченной электроэнергии на привод компрессора (мощность N). КОП=Q/N. Основными параметрами, определяющими КОП, являются t НИТ и воды в системе отопления и ГВС.

Ц икл ТН

6. Изотермический, изобарный, изохорный, адиабатный и политропный процессы идеального газа. Определения, уравнения, изображения в p-V и t-s диаграммах.

Изотермическим наз-ся равновесный пр-с протекающий при постоянной температуре.

U₂- U₁=C₂(T₂-T₁)=0 , т.к. Т=const , т.е. внутренняя энергия не изменяется, и аналогичное выражение первого з-на термодинамики принимает вид:

q=L=_v1∫^v2PdV= _v1∫^v2RT/V dV = RT _v1∫^v2dV/V = RT ln (V2/V1)

Изменение энтропии ΔS_T=S₂ – S₁= R·ln V2/V1= R·ln P1/P2

Определить кол-во теплоты, подведенное к рабочему телу при изотермическом процессе, с использованием удельной теплоемкости невозможно, т.к. С=dq/dT. dT=0 и теплоемкость С=±∞.

И зобарный называется равновесный процесс, протекающий при постоянном давлении.

Работа изменения объема выражается L= _v1∫^v2 P dV= P ·(V2-V1)=R(T2-T1)

Количество теплоты в изобарном процессе может быть определено по ур-ю 1-го закона

q= U2-U1+L= C_v(T2-T1)+R(T2-T1)= (C_v+R) · (T2-T1)= C_p· (T2-T1)= h2-h1

Таким образом вся подводимая теплота расходуется на изменение энтальпии газа.

Изменение энтропии при P=const Δ S_p= S₂ -S₁ =C_p lnT2/T1 T=T1 exp ((S-S₁)/ C_p)

Изохорным называется равновесный процесс, протекающий при постоянном объеме.

dq= dU + P dV; dV=0; dq=dU= C_vdT=U2-U1= C_v (T2-T1)

Следовательно в изохорном процессе вся подводимая теплота расходуется на изменение внутренней энергии газа, а работа расширения равна 0.

Изменение энтропии равно: ΔS_v= S₂- S₁= C_v ln (T2/T1) T=T1 exp ((S-S₁)/ C_v)

Адиабатный наз-ся процесс протекающий без теплообмена м/у термодинамической системой и окружающей средой.

dq=0 dU+PdV=0 dU=C_v dT C_v dT+PdV=0 (1)

PV=RT : PdV+VdP=RdT dT=(PdV+VdP)/R (C_v /R)(PdV+VdP)+PdV=0 (2)

l'/l=k= C_p/ C_v – показатель адиабаты (3); C_v/R из выражения (2) с учетом соотношения (3) с учетом C_p-C_v =R - ур-е Майера → C_v/R=1/(k-1) → тогда (2) преобразуется в dP/P + k dV/V = 0 → PV^k = const.

L=-ΔU=-(U₂-U₁)=U₁-U₂= -C_v(T2-T1)= C_v (T1-T2)=(R/(k-1)) · (T1-T2) =

= (RT1/(k-1)) · (1–T2/T1)

L=(1/(k-1)) · (P1V1 – P2V2)= (P1V1/(k-1)) · (1-T2/T1)

Энтропия при dq=0 : dS= dq/T=0 S=const

Политропным называется всякий процесс идеального газа в котором теплоемкость является постоянной.

q=C_п(t2-t1) dq=C_пdt= C_pdt - VdP и dq=C_пdt= C_Vdt +PdV из этих уравнений выразим

(C_п - C_p)/ (C_п - C_V) = - (VdP)/(PdV) (C_п - C_p)/ (C_п - C_V) = n n·dV/V=-dP/P

Интегрируя полученное соотношение получим n·lg V2/V1 = lg P1/P2 или PVⁿ = const - уравнение политропного процесса

для изохорного процесса n=±∞;изобарного n=0;изотермического n=1 и адиабатного n=k

Поскольку ур-ие политропы отличается от ур-ия адиабаты только величиной показателя n, то ,очевидно, все соотношения между основными параметрами могут быть представлены формулами, аналогичными адиабатному процессу: P2/P1=(V1/V2)ⁿ ; T2/T1=(V1/V2)^n-1 ; T2/T1=(P2/P1)^(n-1)/n

Теплоемкость политропного процесса равна C_п = C_V(n-k)/(n-1)