1) 19) Решение обратной геодезической задачи

Дано: X_A, Y_A, X_B, Y_B.

Определить: _AB, d_AB.

Решение:

_AB - r = arctg (Y/X),

Контроль: d ^. cos  + X_A = X_B,

d ^. sin  + Y_B = Y_B.

Примеры:

1. Определите координаты точки В, если X_A=Y_A=100м, _AB=315 , d_AB=100м (sin 315 = -0,70711, cos 315 =0,70711).

Решение: X_B=X_A+d_AB ^. cos_AB=170,71 м,

Y_B=Y_A+d_AB ^. sin _AB= 29,29 м.

2. Определите дирекционный угол направления ВС и горизонтальное проложение ВС, если XВ=YВ=1000м, XС=1100м, YС=900м.

Решение:

_ВС r_ВС=arctg{(Y_C-Y_B)/(X_C-X_B)}=45 СЗ,

_ВС=360 -45 =315 ,

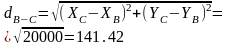
2) Нитяный оптический дальномер

Наиболее распространенным является нитяный дальномер с постоянным параллактическим углом. Он весьма прост по устройству и имеется в зрительных трубах всех геодезических приборов. Сетка нитей таких труб кроме основных вертикальной и горизонтальной нитей имеет дополнительные штрихи (нити), называемые дальномерными. С их помощью по дальномерной рейке определяют расстояние D между точками местности (рис. 56)

 

Рис. 56. Схема определения расстояний оптическим нитяным дальномером

D = D' + f + δ

где D' – расстояние от переднего фокуса объектива до рейки, f – фокусное расстояние объектива, δ - расстояние от оси вращения теодолита до объектива.

Рассмотрим подобные треугольники АВF и а₁b₁F (рис. 56)

ав /АВ = f /D'

где аb = P – расстояние между дальномерными нитями, АВ = n – число сантиметровых делений между дальномерными нитями на рейке. Тогда

D' = f /P ∙ n

D = D' + f + δ = f /P ∙ n + f + δ

Отношение f /P называется коэффициентом дальномера и обозначается K, а сумма (f +δ) – постоянная дальномера и обозначается С.

Тогда

D = K ∙ n + С.

Дальномерные нити наносят так, чтобы при сантиметровых делениях коэффициент дальномера К = 100. Обычно при f объектива равном 200 мм P берут равным 2 мм, тогда K = 100.

В современных теодолитах постоянная дальномера С близка к нулю, поэтому число метров в измеряемом расстоянии равно числу метров в дальномерном отсчете 

D = K ∙ n = 100 ∙ n.

При K = 100 и  n = 124,3 см,  D = 100 ∙ 124,3 см = 124,3 м.

Билет№18

1)Классификация погрешностей (ошибок).

Грубыми наз ошибки превосходящие по обсолютной величине некоторый, установленный для данных условий измерений предел. Ошибки которые по знаку или величине однообразно повторяются в многократных измерениях наз систематическими. Случайные ошибки – это ошибки, размер и влияние которых на каждый отдельный результат измерения остается неизвестным.По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например, ошибка в угле, изм теодолитом, ось вращения которого неточно приведена в вертикальное положение. Внешние ошибки происходят из-зи влияния внешней среды, в которой протекают измерения. Личные ошибки связаны с особенностями наблюдателя.

Свойства случайных погрешностей. Средняя квадратическая погрешность.

Свойства случайных погрешностей:1они не превосходят определенного предела

∆≤3m,2равные по величине,но противоположные по знаку встречаются одинаково часто3малые погрешности чаще встречаются чем большие4среднее арифметическое стремится к 0 при неограниченном возрастание n.Cредняя квадратическая ошибка m, вычисл по формуле m= √(∆²/n) где n число измерений данной величины. Эта формула применима для случаев, когда известно истинное значение измеряемой величины.

2) Методы нивелирования и их точность.

Вид геодезических измерений для определения превышения между точками и высот точек.

Методы нивелирования:

1)Геометрическое нивелирование а)из середины; б)вперед применяют нивелир.

2)Тригонометрическое нивелирование выполняется наклонным лучем применяют Теодолит-тахаметр.

3)Физическое нивелирование основано на использовании различных физических явлении(бараметрическое, гидростатическое )

4) Автоматическое нивелирование используется самописцы передвижные .

Нивелир предназначен для измерения превышений K=100(коэф)

Билет№20

1) Равноточные измерения выполн в одинаковых условиях, одинаковыми по точности приборами и наблюдателями одинаковой квалификации.L₁-x=∆₁ Ln-x=∆n [Ln]-nx=[∆n]

V_i=L_i-x x=[Ln]/n-[∆n]/n кол-во измерений-[∆n]/n=0 тогда Х=[Ln]/n

Арифм средина,средняя квадрат ошибка Арифм средины.

Средне квадрат ошибка подчитывается по ф Бесселя m= √([ ∂²]/(n-1)) где ∂- отклонения отдельных значений измеренной величины от ариф середины, наз вероятнейшими ошибками. Точность ариф середины будет выше точности отдельного измерения. Её средняя квадратич ошибка M опред по ф-ле M=m/√n где m – средняя квадратич ошибка одного измерения.Для повышения контроля и точности опред величину измеряют дважды – в прямом и обратном направлении из двух полученных значений за окончательное принимается среднее из них. В этом случае средняя квадратическая ошибка одного измерения по формуле. m= √[d²]/2n А средний результат из двух измерений – по формуле M=1/2√ [d²]/n где d – разность измеренных величин, n- число разностей ( двойных измерений)