Модель сплошной среды

Гипотеза сплошной среды рассматривает жидкость как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости, и даже малые её частицы, считают состоящими из бесконечно большого числа молекул. Жидкая частица

С точки зрения физики и гидравлики жидкости отличаются от газов тем, что в малых количествах принимают сферическую форму (в виде капли), в больших количествах заполняют лишь ту часть пространства, которая равна её объёму, и может образовывать свободную поверхность. Поэтому их часто называют «капельными», поскольку их объём ничтожно изменяется при воздействии внешних сил, и их чаще всего рассматривают несжимаемыми. Газы же занимают всё предоставленное пространство, его объём значительно изменяется под воздействием внешних сил, что обуславливает его сжимаемость.

Единицы измерения давления.

В международной системе единиц (СИ) основные механические единицы: метр длины, килограмм-массы и секунда. За единицу давления принят Паскаль. Паскаль - это давление, вызываемое силой в один Ньютон (1 Н), равномерно действующей на нормальной к этой силе поверхности площадью один квадратный метр (1 м²). Применяют и укрупненные единицы: кПа и МПа:

1 Па=1 Н/м²=10^-3 кПа=10^-6 МПа.

В технике применяют и систему единиц МКГСС (метр, килограмм-сила, секунда). Единица давления 1 кГс/см², эта величина - техническая атмосфера.

1 кГс/см² = 98066,5 Па ~ 0,98 * 10⁵ Па.

Внесистемной, но часто употребляемой единицей измерения давления является.

Бар (примерно равен одной атмосфере). 1 бар = 10⁵ Па=1,02 кГ/см².

Значение атмосферного давления зависит от высоты над уровнем моря и от состояния воздушной атмосферы. За нормальное атмосферное давление на уровне моря принята физическая атмосфера равная 1,033 кГс/см² , обозначаемая, как 1 атм.

1 атм =101325 Па ≈ 1*10⁵Па.

1. Основные свойства капельных жидкостей

1. Плотностью называется масса вещества, содержащаяся в единице объёма /концентрация массы в пространстве/.

Абсолютная плотность для однородной жидкости равняется М жидкости в объеме V, поделённой на V

ρ = М/V [кг/м³]. (1.1)

ρ = f(p, t).

При НУ, имеем плотности:

- воды - ρ_в = 1000 кг/м³;

- минерального масла - ρ_рж = 880 кг/м³;

- воздуха – ρ_вз = 1,225 кг/м³;

- ртути – ρ_рт = 13600 кг/м³;

- бензина, керосина – ρ = 700…800 кг/м³.

Относительной плотностью называется отношение плотности жидкости при заданной температуре к плотности воды (обозначается δ):

δ = ρ_ж/ρ_в.

Например, для ртути δ_рт = ρ_рт/ρ_в = 13600/1000 = 13,6.

Удельным весом называют вес единицы объёма жидкости. Для однородной жидкости удельный вес равняется величине веса G жидкости, поделенной на объём V, который она занимает

γ = G/V [Н/м³] (1.2)

В системе СИ уд. вес воды при 4ºС составляет γ = ρ_в*g = 1000*9,81 = 9,81*10³ Н/м³.

Связь между удельным весом и плотностью

G = Мg, γV= ρVg, γ = ρ g . (1.3)

2. Сжимаемость (объемная упругость) - свойство изменять объём под действием давления, характеризуется коэффициентом объёмного сжатия, который представляет собой относительное изменение объема ΔV=V₁-V₂ при изменении давления Δp на единицу давления, V₁ – первоначальный объем, V₂ – конечный объем (изотермический процесс).

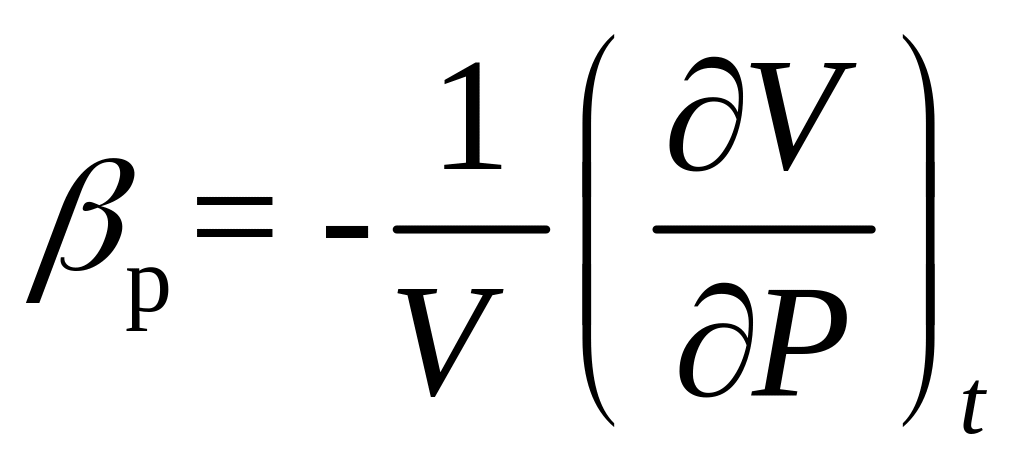
или (1.4)

в системе СИ измеряется в м²/Н или Па^-1.

Увеличению давления Р₂>Р₁ соответствует уменьшение объема V₂<V_1, (поэтому знак минус).

Рассматривая приращения ΔР = Р₂ - Р₁ и ΔV= V₂ - V₁ и, считая β_р =const,

V₂ ≈ V₁ *(1— β_р *ΔP) , (1.5)

и учитывая ρ = m/V, находим приближенную формулу для определения плотности при увеличении давления

ρ₂ ≈ ρ₁ /(1— β_р *Δр) (1.6)

где ρ₂ и ρ₁ — плотности при Р₂ и Р_1.

Объемный модуль упругости (ОМУ) К = 1 / β_р (1.7).

Изменение объёма может быть выражено через ОМУ

V₂ ≈ V₁ *(1—ΔP/К) (1.8)

Размерность ОМУ – Н/м² такая же, как размерность давления.

Используя объёмный модуль упругости К и разности объёмов можно записать зависимость, которую называют обобщённым законом Гука для жидкости.

, (1.9)

К уменьшается с увеличением температуры и растет с повышением давления.

Для воды при атмосферном давлении К_воды = 2000 МПа.

3. Вязкость жидкости - способность жидкости сопротивляться деформации (сдвигу её слоев), свойство противоположное текучести.

Трение при движении вязкой жидкости было открыто Ньютоном, он высказал гипотезу о возникновении касательных напряжений между слоями жидкости.

Кроме обычных подвижных жидкостей существуют очень вязкие жидкости, сопротивление малым деформациям которых значительно, но в состоянии покоя равно нулю. Это реологические жидкости. По мере увеличения вязкости такие жидкости все больше похожи на твёрдое тело. Например, асфальт, гудрон.

Если бочку с горячим асфальтом опрокинуть, он весь вытечет за некоторое время и примет форму лепешки, с течением времени по этой лепешке можно будет ходить, а при ударе она разлетается на куски.

Для медленной деформации обычной жидкости необходимы весьма малые силы, при быстрой деформации жидкость подобно твёрдому телу оказывает значительное сопротивление. Но как только движение жидкости прекращается, это сопротивление исчезает.

При течении вязкой жидкости из-за тормозящего влияния неподвижного дна и трения слои жидкости будут двигаться с разными скоростями, значения которых возрастают при удалении от твёрдого дна. Скорость V тем меньше, чем ближе слой жидкости к неподвижной стенке, при у = 0 , V = 0.

Рассмотрим два слоя жидкости, двигающиеся на расстоянии Δу. Слой А движется со скоростью V, слой В со скоростью V + ΔV. Из-за разности скоростей слой В сдвигается относительно слоя А на величину ΔV(за единицу времени). Величина ΔV является абсолютным сдвигом слоя В, а отношение ΔV/Δy – относительный сдвиг или градиент скорости. При сдвиге аналогично явлению сдвига в твёрдых телах появляются касательные напряжения τ.

Ньютон получил зависимость между касательным напряжением и деформацией (закон жидкостного трения):

τ = μ(ΔV/Δy). T= μS (ΔV/Δy).

Коэффициент μ - динамическая вязкость (характеризует сопротивляемость жидкости сдвигу).

Вывод: напряжения трения возможны только в движущейся жидкости, вязкость проявляется при течении жидкости, в покоящейся жидкости касательные напряжения =0.

В системе СИ μ = «Паскаль- секунда».

В системе СГС единица μ называется «Пуаз» в честь французского врача Пуазейля, исследовавшего законы движения крови в сосудах.

1 Пуаз = 1 (дина*сек)/см². 1 П = 0,1 Па*сек.

При НУ имеем:

- вода μ ≈ 1 сП; - минеральное масло μ ≈ 10 - 1000 сП;

- бензин, керосин μ ≈ 0,5 – 1,0 сП;

- ртуть μ ≈ 1,5 сП; воздух μ ≈ 0,02 сП.

Кинематическая вязкость - отношение динамической вязкости к плотности

υ= μ/ ρ [м²/с]

например вода при t = 20°С имеет кинематическую вязкость 10^-6 м²/с.

В системе СГС единица вязкости равна 1 см²/с и называется Стокс(Ст).

1 м²/с = 10⁴ см²/с(Стокс) =10⁶ сСт - сантиСтокс.

Вязкость капельных жидкостей при увеличении температуры уменьшается.

Вязкость газов, с увеличением температуры возрастает.

Объясняется это различием молекулярного строения. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления.

Обычно влияние температуры на вязкость оценивается с помощью экспериментальных графиков в справочной литературе.

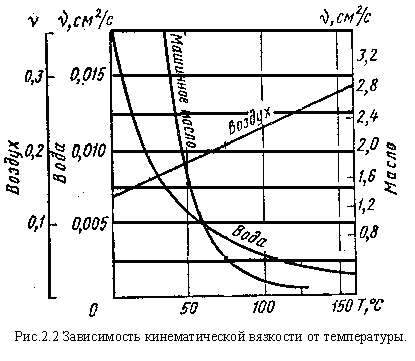
Зависимость вязкости от давления проявляется при давлениях в несколько десятков МПа. С увеличением давления вязкость большинства жидкостей возрастает.

Например, если вязкость воды при давлении 1 атм и 20 ºС принять за единицу, при той же температуре и давлении 100 МПа она вырастет в 4 раза.

4. Температурное расширение характеризуется коэффициентом теплового расширения, который представляет собой относительное изменение объёма при изменении температуры Т на 1°С и постоянном давлении, т.е.

βт =

Рассматривая разности ΔV=V₂—V₁ и ΔТ=Т₂—Т₁ и, принимая βт=const, получаем объем жидкости при изменении температуры

V₂ = V₁ (1+ βт*ΔТ),

и учитывая равенство ρ = М/V, находим приближенную формулу для определения плотности жидкости при изменении температуры

ρ₂ = ρ₁/(1+ βт*ΔТ),

где ρ₂ и ρ₁ — плотности при температурах Т₂ и Т₁.

Для воды коэффициент βт возрастает с увеличением давления и температуры, при Н.У. βт = 200*10^-6, при 100°С и 10 МПа, βт = 700*10^-6.

5. Сопротивление растяжению (прочность жидкости).

Сопротивление растяжению внутри капельных жидкостей по молекулярной теории может быть весьма значительным. При опытах с тщательно очищенной и дегазированной водой в ней были получены кратковременные напряжения растяжения до 23—28 МПа. Однако, технически чистые жидкости, содержащие взвешенные твердые частицы и мельчайшие пузырьки газов, не выдерживают даже незначительных напряжений растяжения. Поэтому считают, что напряжения растяжения в капельных жидкостях невозможны.

6. Растворимость газов в жидкостях характеризуется количеством растворенного газа в единице объема жидкости. Она различна для разных жидкостей и изменяется с увеличением давления.

Относительный объем газа, растворённого в жидкости до её полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, т. е.

Vг = k Vж (p/ р_о),

где Vг — объем растворённого газа, приведенный к нормальным условиям, (р_о, Т₀); Vж - объем жидкости; k — коэффициент растворимости; p - давление жидкости.

Коэффициент k имеет следующие значения при 20 °С:

- для воды k = 0,016;

- для керосина k = 0,13;

- для минеральных масел k = 0,08 – 0,1.

При понижении давления выделяется растворенный в жидкости газ, причём интенсивнее, чем растворятся в ней. Это явление может отрицательно сказываться на работе гидросистем.

7.Силы поверхностного натяжения.

На поверхности раздела жидкости и воздуха действуют силы поверхностного натяжения, стремящиеся придать объему жидкости сферическую форму. Это явление проявляется также при выливании капли жидкости на твердую поверхность.

8. Испаряемость (фазовые превращения) - процесс перехода жидкости в газообразное состояние.

Испаряемость свойственна всем капельным жидкостям, однако, интенсивность испарения неодинакова и зависит от условий, в которых они находятся.

Если объем пространства над жидкостью достаточно велик, испарение продолжается до исчезновения жидкости (выкипание чайника). Если объем недостаточно велик, часть молекул жидкости конденсируется и возвращается в жидкое состояние и испарение продолжается до наступления динамического равновесия, когда число испаряющихся и конденсирующихся молекул выравниваются. В окружающем жидкость пространстве устанавливается давление, называемое давлением насыщенных паров Р_нп.

Давление насыщенных паров Р_н.п. – давление, при котором начинается кипение жидкости при данной температуре. Чем больше давление насыщенных паров при данной температуре, тем больше испаряемость жидкости. С увеличением температуры давление Р_н.п увеличивается, однако, у разных жидкостей в разной степени. Точка кипения t₀ это t при которой жидкость закипает при данном p