Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Житомирский государственный университет им. Ивана Франко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Геометрія 13-14 1.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

2.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Прямі і площини Перша частина

114. Усі вершини ромба належать площині . Пряма паралельна прямій . Як можуть бути розташовані пряма і площина ? Виберіть правильне твердження.

А) пряма може належати площині або перетинати її, пряма не може бути паралельною площині ;

Б) пряма може належати площині , пряма не може перетинати площину або бути паралельною площині ;

В) пряма може належати площині або бути паралельною площині , пряма не може перетинати площину ;

Г) пряма може належати, бути паралельною площині або перетинати площину .

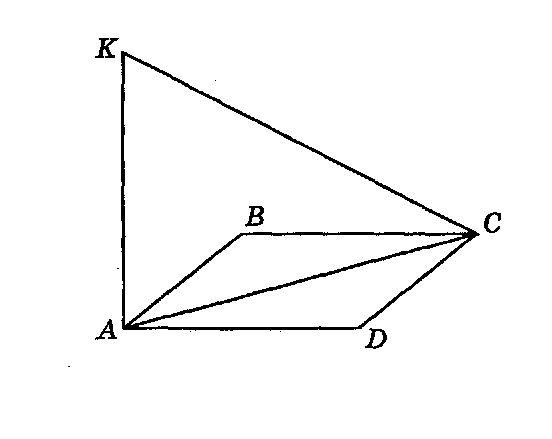
115. Пряма перпендикулярна до площини квадрата

, Знайдіть

А) Б) В) Г)

116. Скільки різних площин можна провести через три точки, які лежать на одній площині?

А) одну; Б) дві; В) три; Г) безліч.

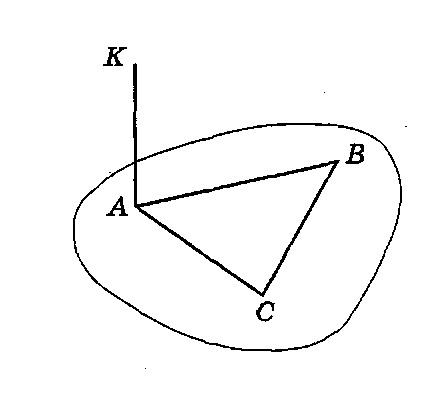
117. Пряма проходить через вершину

Який кут утворює пряма

із площиною

А) Б) В) Г) неможливо

визначити.

118. Сторона паралельна площині , а сторони і перетинають площину в точках і відповідно. Знайдіть , якщо:

А) ; Б) ; В) ; Г)

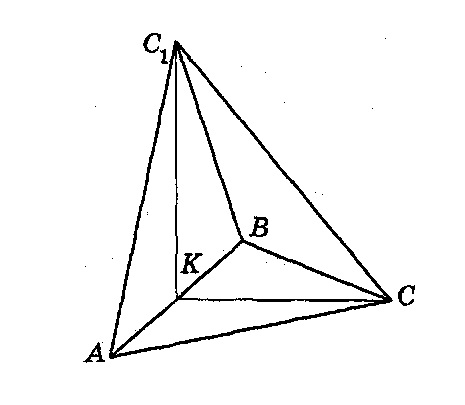
119. Площини рівних рівносторонніх трикутників

і перпендикулярні,

Знайдіть висоту .

А) 4 см; Б) 3 см; В) 2 см; Г) см

120. Сторона паралелограма належить площині а сторона не належить цій площині. Скільки спільних точок мають пряма і площина

А) жодної; Б) одну; В) дві; Г) безліч.

121. Площини прямокутників і перпендикулярні. Скільки спільних точок мають пряма і площина

А) жодної; Б) одну; В) безліч; Г) неможливо визначити.

122. Прямі і паралельні у просторі, а пряма перетинає пряму . Як можуть бути розташовані прямі і ? Виберіть правильне твердження.

А) прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинаються;

Б) прямі і можуть перетинатися, не можуть бути паралельними або мимобіжними;

В) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинаються;

Г) прямі і можуть перетинатися або бути мимобіжними, не можуть бути паралельними.

123. Пряма перпендикулярна до площини а пряма перетинає площину , але не є перпендикулярною до неї. Як можуть бути розташовані прямі і ? Виберіть правильне твердження.

А) прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинатися;

Б) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинатися;

В) прямі і можуть перетинатися, не можуть бути паралельними або мимобіжними;

Г) прямі і можуть перетинатися або бути мимобіжними, не можуть бути паралельними.

124. Яке з тверджень правильне?

А) через три точки завжди можна провести лише одну площину;

Б) через три точки завжди можна провести лише дві площини;

В) через три точки завжди можна провести безліч площин;

Г) через три точки завжди можна провести одну або безліч площин.

125. - перпендикуляр, - похила, проведені з точки до площини . Порівняйте і .

А) ; Б) ; В) ; Г) порівняти неможливо.

126. Площини і перетинаються по прямій . Пряма належить площині . Як можуть бути розташовані прямі і ? Виберіть правильне твердження.

А) прямі і можуть перетинатися, не можуть бути паралельними або мимобіжними;

Б) прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинатися;

В) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинатися;

Г) прямі і можуть перетинатися або бути паралельними, не можуть бути мимобіжними.

127. Площини квадратів і перпендикулярні, . Знайдіть відстань між точками і .

А) ; Б) ; В) ; Г)

128. Площини і паралельні. Точка не належить жодній з площин. Скільки існує прямих, які проходять через точку паралельно площинам і ?

А) жодної; Б) одна; В) дві; Г) безліч.

129. З точки до площини проведено перпендикуляр і похилу . Знайдіть , якщо = 5см, = 4см.

А) ; Б) ; В) ; Г)

130. Пряма паралельна площині , пряма - належить площині . Як можуть бути розташовані прямі і ? Виберіть правильне твердження.

А) прямі і можуть бути паралельними, не можуть бути мимобіжними або перетинатися;

Б) прямі і можуть бути мимобіжними, не можуть бути паралельними або перетинатися;

В) прямі і можуть перетинатися, не можуть бути паралельними або мимобіжними;

Г) прямі і можуть бути паралельними або мимобіжними, не можуть перетинатися.

131. З точки до площини проведено похилі і та перпендикуляр , Знайдіть .

А) ; Б) ; В) ; Г)

132. Прямі і не паралельні і не перетинаються. Скільки площин можна провести через ці дві прямі?

А) жодної; Б) одну; В) дві; Г) безліч.

1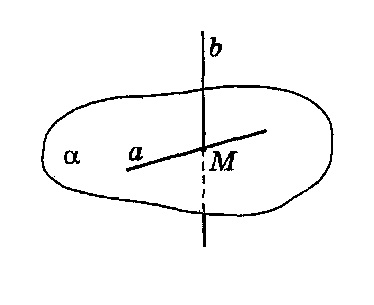 33. Пряма перпендикулярна до площини , а пряма

лежить у площині і проходить через точку

перетину прямої і площини . Яким є кут між

прямими і .

А) Б) В) Г) неможливо визначити.

Прямі і площини

Частина друга

134. Площина паралельна стороні та перетинає сторони і відповідно в точках і . Знайдіть , якщо

135. Два відрізки впираються своїми кінцями у дві паралельні площини. Довжини відрізків дорівнюють і , а їхні проекції на одну з площин відносяться як . Знайдіть відстань між даними площинами.

136. Площини і паралельні. Через точку , яка лежить між цими площинами, проведено прямі і , які перетинають площину у точках і , а площину - у точках і . Знайдіть довжину відрізка , якщо = і .

137. З точки до площини проведено дві рівні похилі по кожна . Кут між похилими дорівнює , а кут між їхніми проекціями - прямий. Знайдіть відстань від точки до площини .

138. Через кінець відрізка проведено площину . Через кінець і точку цього відрізка проведено паралельні прямі, які перетинають площину в точках і відповідно. Знайдіть довжину відрізка , якщо і .

139. Точка знаходиться поза площиною прямокутного , у якого , і на однакових відстанях від його вершин. Знайдіть цю відстань, якщо відстань від точки до площини трикутника дорівнює .

Прямі і площини

Частина третя

140. Кінці відрізка належать двом перпендикулярним площинам. Проекції відрізка на кожну з площин відповідно дорівнюють і . Відстань між основами перпендикулярів, що проведено з кінців відрізка до площин - . Знайдіть довжину даного відрізка.

141. Із кінців відрізка, що належать двом перпендикулярним площинам до лінії перетину площин, проведено перпендикуляри, довжини яких і . Відстань між основами проведених перпендикулярів дорівнює . Обчисліть кути, що утворює цей відрізок з даними площинами.

Многогранники. Призма

Перша частина

142. Об’єм призми дорівнює , а площа основи - . Знайдіть висоту призми.

А) ; Б) ; В) ; Г)

143. Який із запропонованих чотирикутників не може бути основою паралелепіпеда?

А) трапеція; Б) квадрат; В) прямокутник; Г) ромб.

144. Який многогранник є основою призми, якщо вона має рівно 24 ребра?

А) шестикутник; Б) восьмикутник; В) десятикутник; Г) дванадцятикутник.

145. У правильній чотирикутній призмі сторона основи дорівнює , а площа повної поверхні призми - . Знайдіть висоту призми.

А) ; Б) ; В) ; Г)

146. Сторони основи прямокутного паралелепіпеда дорівнюють і , а діагональ однієї з бічних граней - Знайдіть об’єм прямокутного паралелепіпеда.

А) ; Б) ; В) ; Г)

147. У чотирикутній призмі площа основи дорівнює , а площа кожної з бічних граней - . Знайдіть площу повної поверхні призми.

А) ; Б) ; В) ; Г)

148. Знайдіть об’єм прямокутного паралелепіпеда, лінійні розміри якого дорівнюють , і

А) ; Б) ; В) ; Г)

149. Сторони основи прямокутного паралелепіпеда дорівнюють і , а діагональ паралелепіпеда - Знайдіть площу повної поверхні паралелепіпеда.

А) ; Б) ; В) ; Г)

150. Сторони основи прямого паралелепіпеда дорівнюють і та утворюють між собою кут . Знайдіть об’єм паралелепіпеда, якщо його бічне ребро дорівнює .

А) ; Б) ; В) ; Г)

151. Площа основи трикутної прямої призми дорівнює , а площі бічних граней - , і . Знайдіть площу повної поверхні призми.

А) ; Б) ; В) ; Г)

152. У правильній чотирикутній призмі сторона основи дорівнює , а бічне ребро - . Знайдіть площу діагонального перерізу призми.

А) ; Б) ; В) ; Г)

153. У правильній чотирикутній призмі сторона основи дорівнює , а бічне ребро - . Знайдіть площу бічної поверхні призми.

А) ; Б) ; В) ; Г)

154. Знайдіть об’єм правильної чотирикутної призми, сторона основи якої дорівнює , а висота - .

А) ; Б) ; В) ; Г)

155. У правильній трикутній призмі сторона основи дорівнює , а діагональ бічної грані - . Знайдіть площу бічної поверхні призми.

А) ; Б) ; В) ; Г)

156. Скільки всього ребер у п’ятикутної призми?

А) ; Б) ; В) ; Г)

Многогранники. Призма

Частина друга

157. В основі похилої призми лежить рівносторонній трикутник зі стороною . Одна з вершин верхньої основи рівновіддалена від усіх вершин нижньої основи. Знайдіть висоту призми, якщо її бічне ребро дорівнює .

158. Діагональ прямокутного паралелепіпеда дорівнює і нахилена до площини основи під кутом . Знайдіть об’єм паралелепіпеда, якщо кут між діагоналями його основи дорівнює .

159. Основою прямого паралелепіпеда є ромб з гострим кутом і стороною . Більша діагональ паралелепіпеда нахилена до площини основи під кутом . Знайдіть площу бічної поверхні паралелепіпеда.

160. Основою похилої призми є квадрат зі стороною . Одна з вершин верхньої основи рівновіддалена від усіх вершин нижньої основи. Знайдіть об’єм призми, якщо бічне ребро її утворює з площиною основи кут .

161. Основою прямої призми є ромб з тупим кутом . Площа бічної поверхні призми дорівнює , а площа її повної поверхні - . Знайдіть висоту призми.

162. Основою прямого паралелепіпеда є ромб з периметром і діагоналлю . Більша діагональ паралелепіпеда дорівнює . Знайдіть об’єм паралелепіпеда

163. Основою прямої призми є рівнобедрений трикутник з основою і бічною стороною . Через основу цього трикутника проведено переріз, який утворює кут з площиною основи і перетинає бічне ребро. Знайдіть площу цього перерізу.

164. У прямій трикутній призмі сторони основи дорівнюють , і . Через бічне ребро призми та середню за довжиною висоту основи проведено переріз, площа якого . Знайдіть об’єм призми.

165. Знайдіть площу повної поверхні прямокутного паралелепіпеда, якщо його діагональ більша за лінійні виміри відповідно на , і .

166. Основою прямого паралелепіпеда є паралелограм зі сторонами і та гострим кутом . Знайдіть об’єм паралелепіпеда, якщо його повна поверхня дорівнює

Многогранники. Призма

Частина третя

167. Основою прямої призми є паралелограм зі сторонами і . Одна з діагоналей призми дорівнює , а інша - . Знайдіть площу бічної поверхні цієї призми.

168. Основою прямої призми є рівнобічна трапеція з тупим кутом , в яку можна вписати коло. Діагональ бічної грані, що містить бічну сторону трапеції дорівнює і нахилена до площини основи під кутом . Знайдіть повну поверхню призми.

169. Основою прямого паралелепіпеда є ромб. Площа бічної поверхні паралелепіпеда дорівнює , а площа одного з його діагональних перерізів дорівнює . Знайдіть площу другого діагонального перерізу паралелепіпеда.

170. Найбільша діагональ правильної шестикутної призми дорівнює і утворює з бічним ребром призми кут . Знайдіть об’єм призми.

171. Основою прямої призми є ромб. Переріз призми площиною проведено через більшу діагональ її нижньої основи та вершину тупого кута верхньої основи і. утворює з площиною нижньої основи кут . Перерізом є трикутник, кут якого при вершині верхньої основи призми дорівнює , а площа . Знайдіть об’єм призми.

172. Основою прямої призми є прямокутний трикутник, гострий кут якого дорівнює , а гіпотенуза дорівнює . Діагональ грані, що містить катет, протилежний даному куту і утворює з площиною основи призми кут . Знайдіть об’єм призми.

173. Основою прямої призми є ромб, сторона якого дорівнює . Кут між площинами двох бічних граней призми дорівнює . Більша діагональ призми нахилена до площини основи під кутом . Знайдіть об’єм призми.

174. Сторона основи правильної чотирикутної призми вдвічі менша за її бічне ребро. Через сторону основи та середину протилежного до неї бічного ребра проведено переріз.. Знайдіть площу бічної поверхні призми, якщо радіус кола, описаного навколо перерізу призми дорівнює .

175. Основою прямої призми є ромб. Площі діагональних перерізів призми дорівнюють і .Менша діагональ призми утворює з площиною основи кут . Знайдіть повну поверхню призми.

176. Через діагональ нижньої основи і протилежну вершину верхньої основи правильної чотирикутної призми проведено переріз.. Кут нахилу перерізу до основи дорівнює . Знайдіть об’єм призми, якщо площа перерізу дорівнює .

177. Діагональ прямокутного паралелепіпеда утворює з площиною однієї бічної грані кут , а з площиною іншої - кут .Знайдіть площу бічної поверхні паралелепіпеда, якщо його діагональ дорівнює .

178. Основою прямої призми є рівнобедрений трикутник. Діагоналі бічних граней, що містять бічні сторони цього трикутника і мають спільну вершину дорівнюють і утворюють між собою кут . Площина, яка проходить через ці діагоналі,. нахилена до площини основи під кутом . Знайдіть об’єм призми.

179. Бічні грані правильної шестикутної призми - квадрати. Знайдіть кут між прямими, одна з яких містить діагональ бічної грані, а друга сторону основи, яка перетинає цю діагональ.

180. Основою прямої призми є трикутник зі стороною і прямими до неї кутами та . Діагональ бічної грані, що містить цю сторону, утворює з площиною основи кут . Знайти об’єм призми.

181. Основою прямої призми є рівнобічна трапеція з діагоналлю і гострим кутом . Діагоналі трапеції перпендикулярні до її бічних сторін. Знайдіть об’єм призми, якщо її діагональ утворює з площиною основи кут .

182. Площа бічної поверхні правильної трикутної призми в 12 разів більша за площу основи. Знайдіть кут між діагоналлю бічної грані та площиною основи призми.

183. Основою прямої призми є прямокутник з кутом між діагоналями. Діагональ призми дорівнює і утворює з площиною основи кут . Знайти об’єм призми.

184. Кут між діагоналями основи прямокутного паралелепіпеда дорівнює . Діагональ паралелепіпеда утворює із площиною основи кут . Знайдіть висоту паралелепіпеда, якщо його об’єм дорівнює .

185. Основою прямої призми є рівнобедрений трикутник з кутом при вершині та радіусом описаного кола . Діагональ бічної грані, що містить бічну сторону цього трикутника, утворює з площиною основи кут .Знайдіть об’єм призми.

Піраміда

Перша частина

186. Піраміда має рівно дев’ять граней. Скільки сторін має многокутник, який є основою піраміди?

А) ; Б) ; В) ; Г)

187. Сторона основи правильної чотирикутної піраміди дорівнює , а висота - . Знайдіть площу діагонального перерізу цієї піраміди.

А) ; Б) ; В) ; Г)

188. Основою піраміди є ромб зі стороною і висотою . Знайдіть об’єм піраміди, якщо її висота дорівнює .

А) ; Б) ; В) ; Г)

189. Знайдіть об’єм піраміди, основою якої є квадрат зі стороною , а висота піраміди дорівнює .

А) ; Б) ; В) ; Г) .

190. Знайдіть площу бічної поверхні правильної шестикутної піраміди, якщо площа однієї бічної грані дорівнює .

А) ; Б) ; В) ; Г) .

191. Основою піраміди є прямокутник зі сторонами і , а основою висоти піраміди є точка перетину діагоналей цього прямокутника. Знайдіть висоту піраміди, якщо її бічне ребро дорівнює .

А) ; Б) ; В) ; Г)

192. Сторона основи правильної чотирикутної піраміди дорівнює , а апофема - . Знайдіть площу бічної поверхні піраміди.

А) ; Б) ; В) ; Г)

193. Сторона основи правильної трикутної піраміди дорівнює , а висота - . Знайдіть площу перерізу піраміди, що проходить через її висоту і бічне ребро.