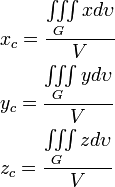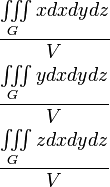1.13 Вычисление длин дуг.
а)
Длина дуги гладкой (непрерывно
дифференцируемой) кривой
равна
б)
Если кривая С задана параметрическими
уравнениями
и
,
где
- непрерывно дифференцируемые на отрезке
,
то длина дуги кривой С выражается
формулой
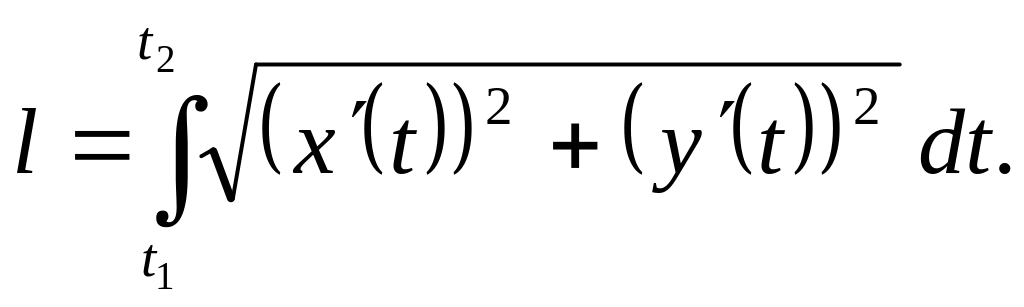
в)
Если кривая С задана в полярных координатах
уравнением
,
где
- непрерывно дифференцируемая на отрезке
функция, то длина дуги соответствующей
кривой равна
1.14 Вычисление объемов
а)
Если объем тела существует и
есть площадь сечения тела плоскостью,
перпендикулярной оси Ox
в точке x,
то
б) Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции
,
где
- непрерывная функция, равен
В
более общем случае, объем кольца,
образованного вращением вокруг оси Ox
фигуры
,
где
- непрерывные неотрицательные функции,
равен
Объем тела, образованного вращением вокруг оси Oy плоской фигуры
где - непрерывная функция, равен
Двойной интеграл
1. Основные понятия и определения
О
пределение.
1. Пусть в замкнутой области (области с границей) D плоскости хОу задана непрерывная функция z=ƒ(х;у).
2. Разобьем область
D на n «элементарных областей» 
,
площади которых обозначим через ΔSi,
а диаметры (наибольшее расстояние
между точками области) - через di..
3. В каждой области Di выберем произвольную точку Mi (xi;yi), умножим значение ƒ(хi;уi) функции в этой точке на ΔSi и составим сумму всех таких произведений:
(1)
Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.
4. Рассмотрим предел
интегральной суммы (1), когда n стремится
к бесконечности таким образом, что max
di
0. Если этот предел существует, конечен
и не зависит ни от способа разбиения
области D на части, ни от выбора точек в
них, то он называется двойным
интегралом от функции ƒ(х;у) по области
D и обозначается
(или
)
Таким образом, двойной интеграл определяется равенством
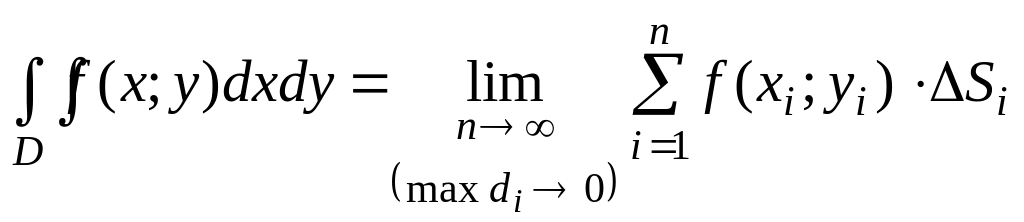(2)
В этом случае функция ƒ(х;у) называется интегрируемой в области D; D - область интегрирования; х и у - переменные интегрирования; dxdy (или dS) - элемент площади.
Для всякой ли функции существует двойной интеграл? Каковы необходимые и достаточные условия его существования?
Теорема 1 (необходимое условие интегрируемости функции).
Если функция z=ƒ(х; у) интегрируема по области D, то она ограничена в этой области.
Теорема 2 (достаточное условие интегрируемости функции).
Если функция z=ƒ(х; у) непрерывна в ограниченной замкнутой области D, то она интегрируема по этой области.
На самом деле, функция интегрируема при менее жестких ограничениях:
Теорема 3.
Ограниченная функция, имеющая конечное число точек и линий (спрямляемых, т.е. конечной длины) разрыва в области D, интегрируема по этой области.
2. Основные свойства двойного интеграла
Перечислим без доказательства основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
1).
-
линейность
2).
- линейность.
3). Если область D
разбить линией на две области D1 и D2
такие, что
,
а пересечение D1 и D2 состоит
лишь из линии, их разделяющей, то
-
аддитивность.
4). Если в области
D имеет место неравенство ƒ(х; у)
0,
то и
.
Если в области D функции ƒ(х;у) и
(х;у)
удовлетворяют неравенству
,
то и
интегрирование неравенств.
5).
,
Так как
.
6). Если функция
ƒ(х; у) непрерывна в замкнутой области
D, площадь которой S, то
,
где m и М - соответственно наименьшее и
наибольшее значения подынтегральной
функции в области D.
7). Если функция
ƒ(х;у) непрерывна в замкнутой области
D, площадь которой S, то в этой области
существует такая точка (хо; уо),
что
.
Величину
называют
средним значением функции ƒ(х; у) в
области D.
3. Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
1. Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а и х=b и кривыми у=φ1(x) и у=φ2(х), причем функции φ1(x) и φ2(х) непрерывны и таковы, что φ1(x) ≤ φ2(х) для всех х є [а; b] (см. рис). Такая область называется правильной в направлении оси Оy
Определение.
Назовем область D правильной в направлении оси Оy, если она
1. ограничена:
сверху — графиком только одной функции
,
снизу — графиком только одной функции
.
2. любая прямая, параллельная оси Oy и проходящая через внутреннюю точку области D пересекает ее границу только в двух точках.
При таких областях интегрирования, двойной интеграл вычисляется по формуле:
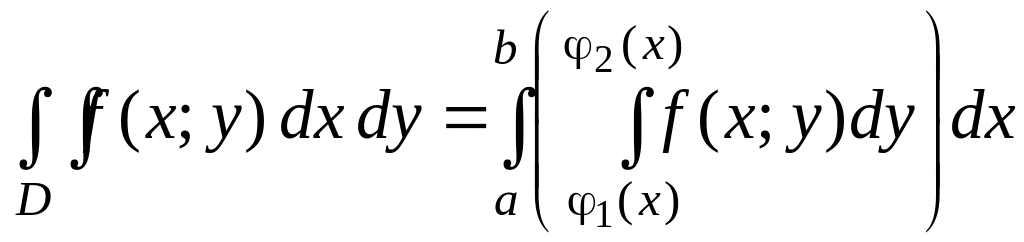(3)
Формула (3) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (3) называют двукратным (или повторным) интегралом от функции ƒ(х; у) по области D.
При этом
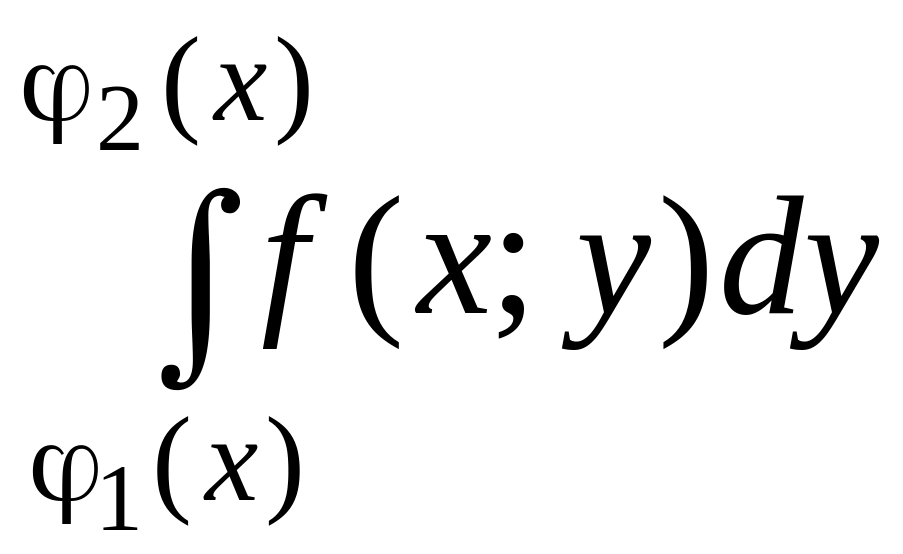называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
2. Если же область D ограничена прямыми y=c и y=d (c<d), кривыми x=Ψ1(у) и х=Ψ2(у), причем Ψ1(у)≤Ψ2(у) для всех у є [с; d], т. е. область D - правильная в направлении оси Оx, то аналогично получим:
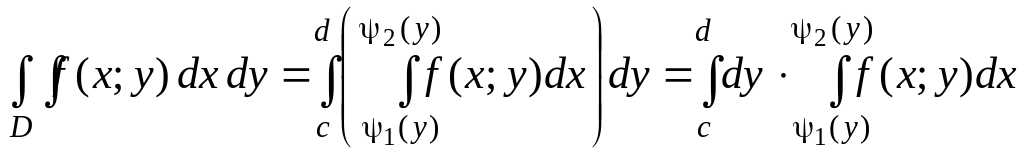(4)
Замечания.
1. Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (3), так и по формуле (4).
2, Если область D не является правильной (верхняя или нижняя граница интегрирования внутреннего интеграла не записывается одной формулой, или любая прямая, параллельная оси Oy (Ox) и проходящая через внутреннюю точку области D пересекает ее границу более, чем в двух точках), то для сведения двойного интеграла к повторным область D следует разбить на части, правильные в направлении оси Оу или оси Ох.
3. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные. Внутренние пределы постоянны только для координатного прямоугольника. Внутренние пределы интегрирования могут зависеть только от внешней переменной.
Примеры.
1. Вычислить
повторный интеграл
(Отв.
)
2. По какой переменной взят внешний интеграл? Написать уравнения кривых, ограничивающих область интегрирования и построить эту область:
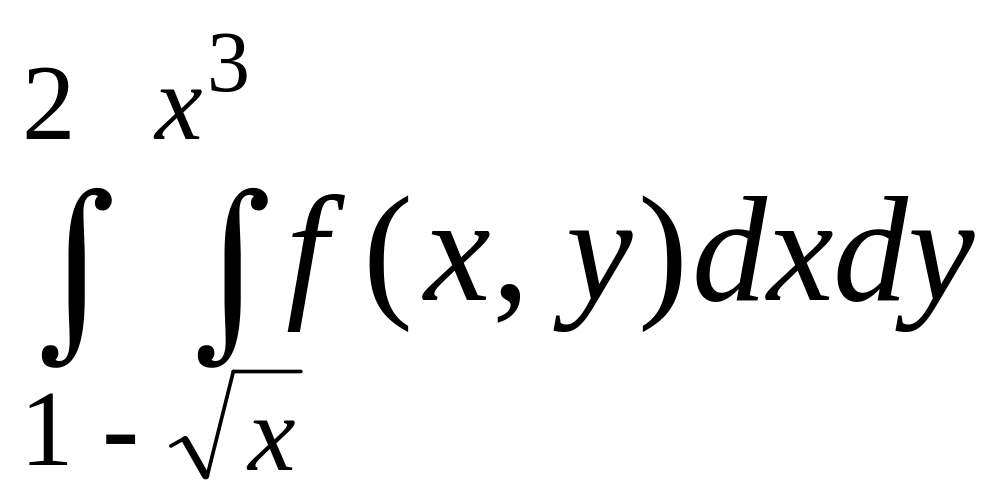
3. D:
у = х, у = х-3, у = 2, у = 4. Записать
в виде повторных в различных порядках.
4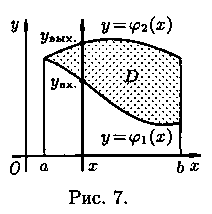
.
Изменить порядок интегрирования:
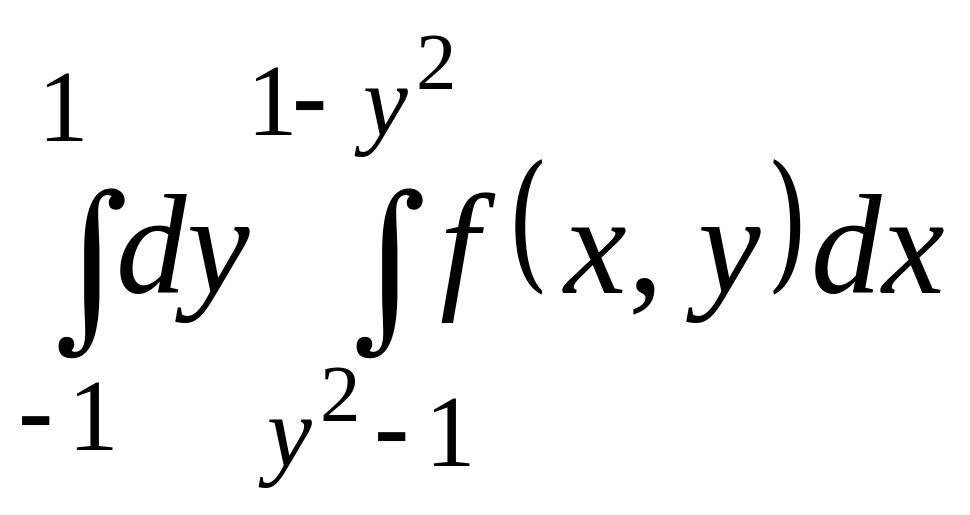
5. Вычислить
,
где область D: у =x2, у=0, х+у-2=0.
4. Замена переменных. Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
и
(5)
Если функции (5) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
,
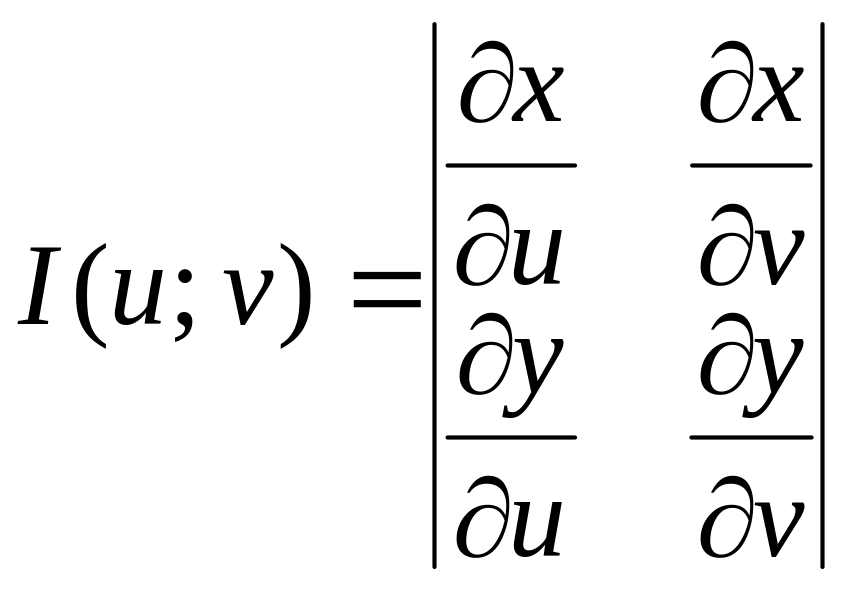(6)
а функция ƒ(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
(7)
Функциональный определитель (6) называется определителем Якоби или якобианом (Г.Якоби - немецкий математик). Доказательство формулы (7) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами r и .
В качестве u и υ возьмем полярные координаты r и . Они связаны с декартовыми координатами формулами х=rcos , у=r sin .
Правые части в этих равенствах - непрерывно дифференцируемые функции. Якобиан преобразования определяется из (6)
.
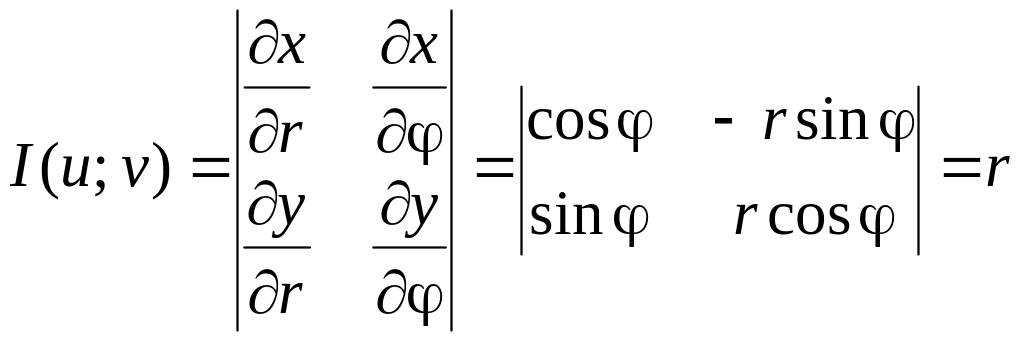Формула замены переменных (7) принимает вид:
(8)
где D* - область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу.
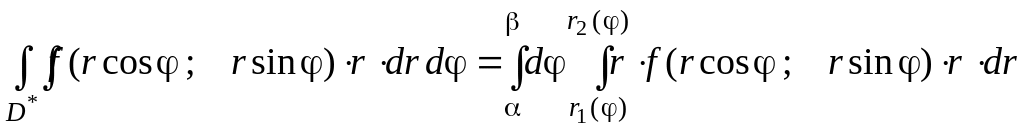(9)
Замечания.
1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид ƒ(х2+у2); область D есть круг, сектор, кольцо. При расстановке пределов в полярных координатах r обычно считают внутренней переменной, а φ − внешней.
2. В случае
эллиптической области выгоднее
использовать обобщенные полярные
координаты: х=arcos,
у=brsin, dxdy=abrdr
d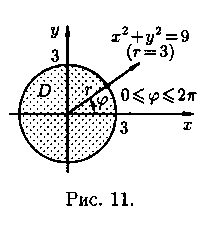
.
Пример.
Вычислить
,
где область D - круг
.
Решение: Применив формулу (8), перейдем к полярным координатам:
Область D в полярной системе координат определяется неравенствами (см. рис) 0≤≤2,0≤r≤3. Заметим: область D - круг - преобразуется в область D* - прямоугольник. Поэтому, согласно формуле (9), имеем:
.
5. Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
1. Объем тела (геометрический смысл двойного интеграла)
Объем цилиндрического тела находится по формуле
(10)
где z=ƒ(х; у)>=0 - уравнение поверхности, ограничивающей тело сверху.
2. Площадь плоской фигуры
Если положить в формуле (10) ƒ(х; у)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
(11)
3. Масса плоской фигуры (физический смысл двойного интеграла)
Масса плоской пластинки D с переменной плотностью =(х; у) находится по формуле
(12)
4. Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу могут быть вычислены по формулам
и
(13)
а координаты центра масс фигуры - по формулам
и
(14)
5. Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. Мl = m•d2. Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
и
(15)
Момент инерции фигуры относительно начала координат – по формуле Мо=Мх +Му.
6. Площадь поверхности
Пусть поверхность S задана явным уравнением z=ƒ(х;у). D – её проекция на плоскость хОу. И в этой области функция z=ƒ(х;у) однозначна, непрерывна и имеет непрерывные частные производные первого порядка по х и по у. Тогда
(16)
Пример.
Найти массу,
статические моменты Sx и Sy
и координаты центра тяжести фигуры,
лежащей в первой четверти, ограниченной
эллипсом
и
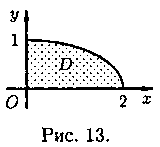координатными осями (см. рис). Поверхностная
плотность в каждой точке фигуры =(х;у)=
30 • ху.
Решение: По формуле (12) находим массу пластинки.
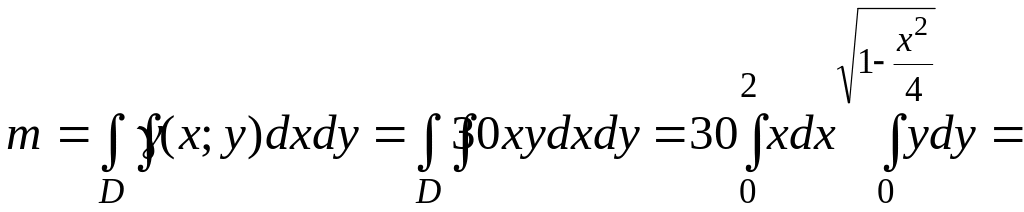
Находим статические моменты
,
и координаты центра тяжести пластинки.
,
.
ТРОЙНОЙ ИНТЕГРАЛ
1. Основные понятия
Теория тройного интеграла аналогична теории двойного интеграла. Поэтому изложим ее в несколько сокращенном виде.
Определение.
Пусть в замкнутой
области V пространства Oxyz задана
непрерывная функция u =ƒ(х; у; z). Разбив
область V сеткой поверхностей на n частей
и выбрав в каждой из них произвольную
точку Мi(хi; yi; zi),
составим интегральную сумму для функции
ƒ(х; у; z) по области V
(здесь ∆Vi –
объем элементарной области Vi).
(1)
Если предел интегральной суммы существует и конечен при неограниченном увеличении числа n таким образом, что каждая «элементарная область» Vi стягивается в точку (т. е. диаметр области di стремится к нулю, т. е. di 0), то его называют тройным интегралом от функции u =ƒ(х; у; z) по области V и обозначают
(или
)
Таким образом, тройной интеграл определяется равенством
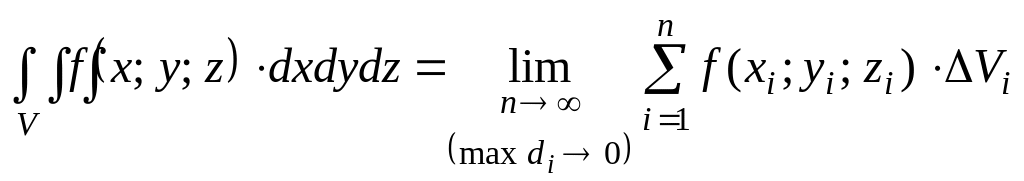(2)
Здесь dv=dx dy dz - элемент объема.
Теорема (существования).
Если функция u=f(x; y; z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (1) при n ∞ и max di 0 существует и не зависит ни от способа разбиения области V на части, ни от выбора точек Мi(хi; yi; zi) в них.
2. Основные свойства тройного интеграла
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
1).
,
линейность.
2).
3). Если область V разбить на две области V1 и V2, такие, что V=V1UV2, а пересечение V1 и V2 состоит лишь из границы, их разделяющей, то
,
аддитивность.
4). Если в области
V функция f(x;y;z)
0,
то и
.
Если в области интегрирования
ƒ(х;у;z)
(x;y;z),
то и
5).
,
так как в случае f(x;y;z)=1, любая интегральная
сумма имеет вид
и
численно равна объему тела.
6). Оценка тройного интеграла:
,
где m и М - соответственно наименьшее и наибольшее значения функции f(x;y;z) в области V. А f(x;y;z) непрерывна в замкнутой области V.
7). Теорема о среднем значении: если функция f(x;y;z) непрерывна в замкнутой области V, то в этой области существует такая точка Mo(xo;yo;zo), что
,
где V - объем тела. f(x0;y0;z0)
– среднее значение функции f(x;y;z) в
области V.
3. Вычисление тройного интеграла в декартовых координатах
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.
Пусть область
интегрирования V является
тело, ограниченное снизу поверхностью
,
сверху – поверхностью
,
причём
и
- непрерывные функции в замкнутой области
D, являющейся проекцией
тела на плоскость Оху.
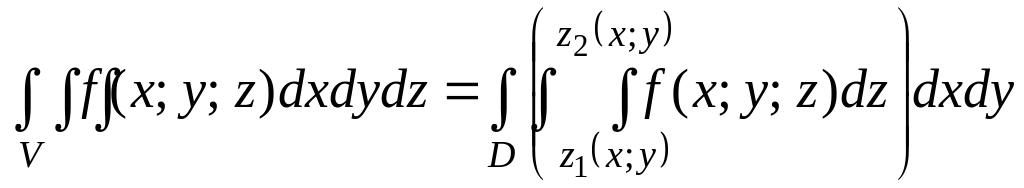
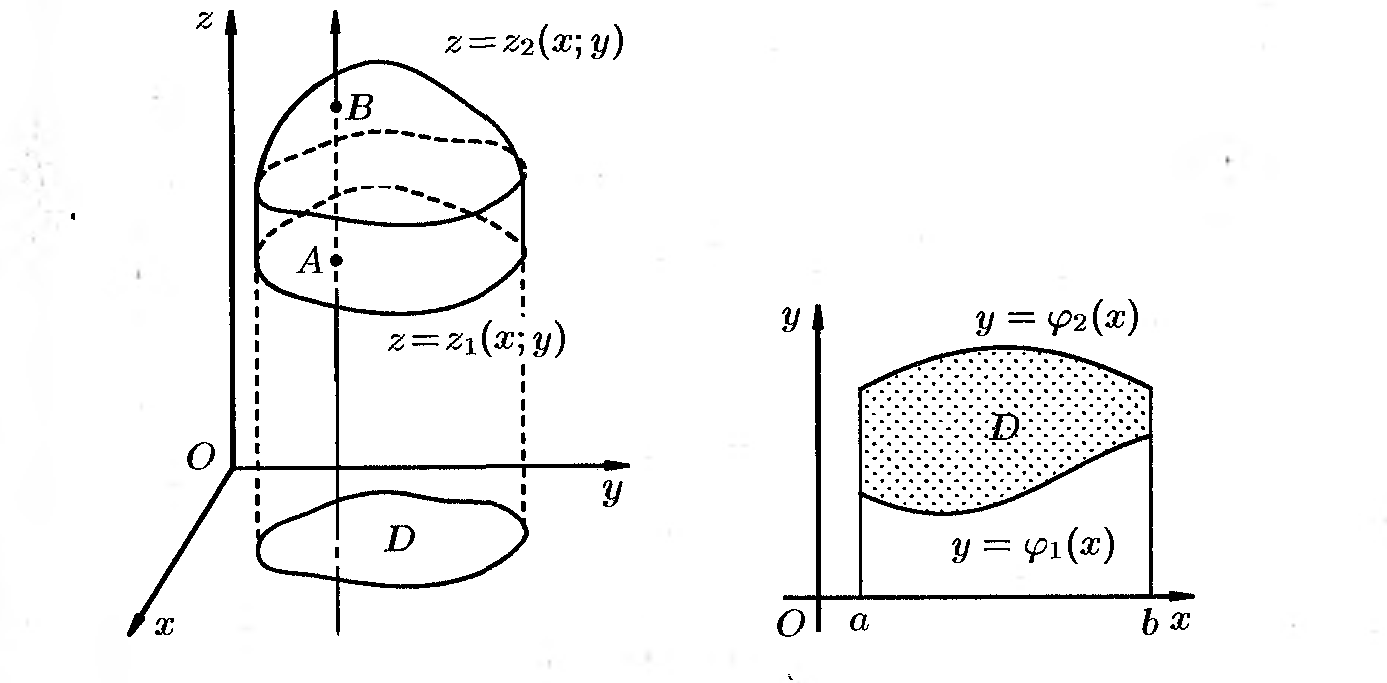
Если область D
ограничена линиями х=а, х=в (а<в), у=
и у=
,
где
и
- непрерывные на отрезке
функции, причём
(см. рис.), то, переходя от двойного
интеграла к повторным, получаем формулу
по которой вычисляется тройной интеграл
в декартовых координатах:
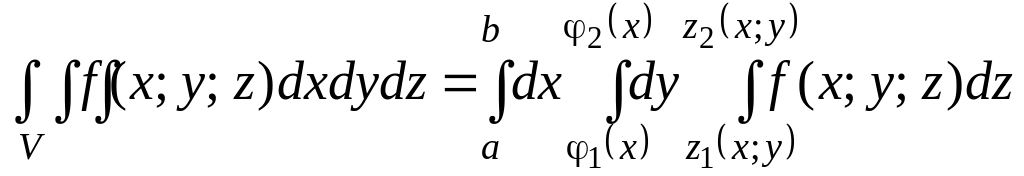(3)
4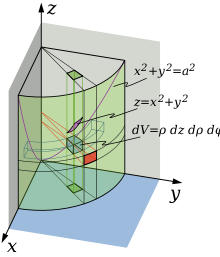
.
Выражение тройного интеграла через
цилиндрические координаты
В некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
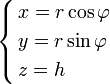(4)
Модуль якобиана
отображения равен
.
Таким образом, получаем, что
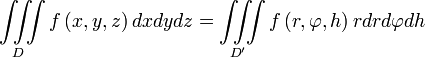(5)
Здесь
является элементом объема в
цилиндрических координатах.
5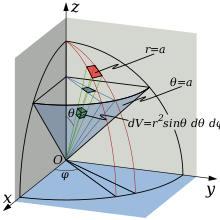
.
Выражение тройного интеграла через
сферические координаты
Кроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
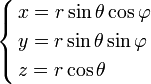(6)
Модуль якобиана
отображения равен
.
Таким образом, получаем, что
(7)
Здесь
является элементом объема в
сферических координатах.
6. Приложения тройных интегралов
Наименование величины |
Общее выражение |
Прямоугольные координаты |
Цилиндрические координаты |
Сферические координаты |
Объем тела |
|
|
|
|
Статические моменты относительно координатных плоскостей |
|
|
|
|
Масса физического тела с плотностью μ |
|
|
|
|
Моменты инерции геометрического тела относительно координатных плоскостей |
|
----------------- |
--------------- |
----------------- |
Моменты инерции геометрического тела относительно координатных осей |
|
---------------- |
-------------- |
--------------- |
Момент инерции геометрического тела относительно оси OZ |
|
|
|
|
Координаты центра тяжести тела |
|
------------------ |
----------- |
------------- |
Координаты центра тяжести однородного тела |
|
|
— |
— |
Задачи.
1. Найти объём тела,
ограниченного параболоидом
и
плоскостью
.
Отв.
.
2. Вычислить
,
где V – область, ограниченная
верхней частью конуса
и плоскостью
.
Отв.
.
3
.
Вычислить
,
где V – область, ограниченная
поверхностями
,
,
.
Решение. Перейдём в интеграле к сферическим координатам по формулам (6). Тогда область интегрирования можно задать неравенствами
.
А, значит,
=…
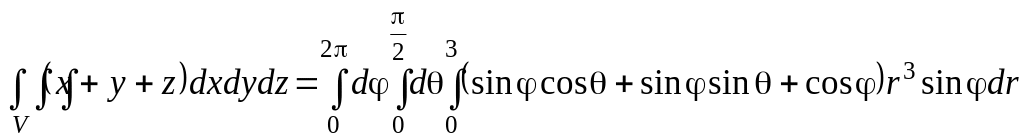Отв.
.