МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное

учреждение высшего

профессионального образования

«Южно-Российский государственный университет экономики и сервиса»

(ФГБОУ ВПО «ЮРГУЭС»)

УТВЕРЖДАЮ

Заведующий кафедрой

«Математика»

И.М.Мальцев

«03» сентября 2012 г.

На правах рукописи

КУРС ЛЕКЦИЙ

«МАТЕМАТИКА (модуль 2)»

для студентов 1-го курса

Учебно-методическое пособие к самостоятельному изучению

отдельных разделов дисциплины «Математика»

Электронный образовательный ресурс

(Для студентов всех форм обучения)

Авторы (составители):

к.т.н., доцент О.А. Алейникова

Рассмотрен и рекомендован

для использования в учебном процессе на 2012/2013 – 2017/2018 уч. г. на заседании Кафедры «Математика». Протокол № 1 от 03 09 2012 г.

Шахты 2012

Интегралы.

Неопределённый интеграл.

1.1 Первообразная и неопределенный интеграл. Пусть Т – некоторый промежуток на числовой оси, на котором заданы функции f(x) и F(x).

Определение. Функция F(x) называется первообразной функции f(x) на промежутке Т, если .

Определение. Пусть функция f задана на промежутке Т. Совокупность всех ее первообразных на этом промежутке называется неопределенным интегралом от функции f и обозначается

.

Если F(x) – какая-либо первообразная функция f на рассматриваемом промежутке, то

,

где С – произвольная постоянная.

1.2 Основные свойства неопределенного интеграла

1) Если функция F(x) дифференцируема на промежутке Т, то

.

2) Пусть функция f(x) имеет первообразную на промежутке Т, тогда справедливо равенство

.

3) Если функция имеют первообразные на промежутке Т, то для любых R функция имеет первообразную на этом промежутке, причем

.

1.3 Таблица интегралов

1) .

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

(если под корнем то ).

1.4 Формула замены переменной. Пусть функции и определены соответственно на промежутках Т и Т₁ , причем Если функция f имеет на Т первообразную F(x) и, следовательно,

а функция дифференцируема на Т₁, то функция имеет на Т₁ первообразную и

(1)

Иначе говоря, сделаем сначала подстановку , а затем возьмем интеграл, или сначала возьмем интеграл, а потом сделаем указанную подстановку, - результат будет один и тот же.

Отметим, что формулу (1) бывает целесообразно использовать и в обратном порядке, т.е. справа налево. Именно, иногда удобно вычисление интеграла с помощью соответствующей замены переменного свести к вычислению интеграла

В случае, когда функция имеет обратную , то воспользовавшись формулой (1) справа налево, сводим вычисление к вычислению Эта формула называется обычно формулой интегрирования заменой переменного.

1.5 Формула интегрирования по частям. Если функции u(x), v(x) дифференцируемы на некотором промежутке, и на этом промежутке существует интеграл то на нем существует и интеграл причем

Эта формула называется формулой интегрирования по частям. Дадим некоторые рекомендации для использования этой формулы. А именно, что целесообразно обозначить под интегралом через функцию u, а что брать в качестве дифференциала dv. Пусть Р(х) – некоторый многочлен. Тогда

1)

2)

3)

4)

5)

6)

Отметим, что при необходимости формулу интегрирования по частям можно применять несколько раз подряд.

1.6 Интегрирование рациональных дробей. Рассмотрим интеграл от рациональной функции. Метод нахождения таких интегралов основан на возможности разложения любой правильной рациональной дроби на сумму элементарных дробей. К элементарным относятся дроби вида

где n – некоторое натуральное число, а трехчлен не имеет действительных корней.

Остановимся подробнее на этапах этого метода.

1) Если дробь неправильная, то поделив числитель на знаменатель, выделим целую часть

при этом степень многочлена меньше степени многочлена .

2) Разложим знаменатель на множители

3) Представим правильную дробь в виде суммы элементарных дробей

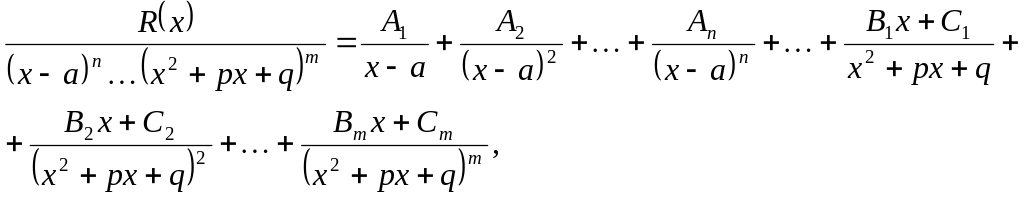
где коэффициенты пока не определены.

4) Находим в последнем разложении неизвестные коэффициенты и сводим тем самым интеграл к вычислению суммы интегралов от элементарных дробей.

1.7 Интегралы вида

а) В общем случае интегралы вида где - рациональная функция двух переменных, сводятся к интегралу от рациональной функции одной переменной путем универсальной тригонометрической подставки , . Действительно,

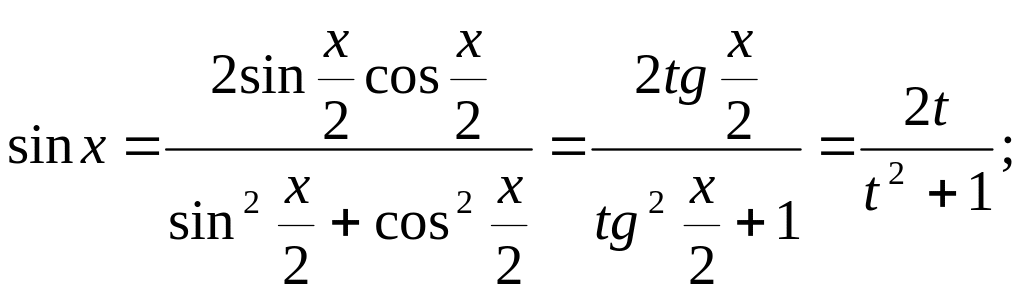
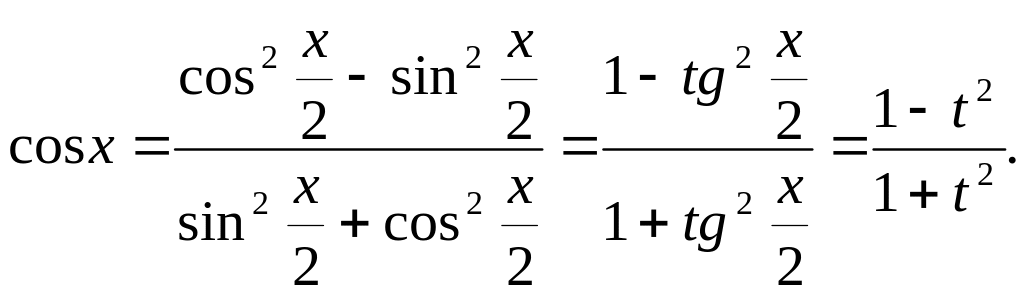
Из равенства следует, что и

Тогда

б) Если подынтегральная функция имеет вид но и входят только в четных степенях (допускается наличие произведения ), то удобно применять подстановку или .

В этом случае

.

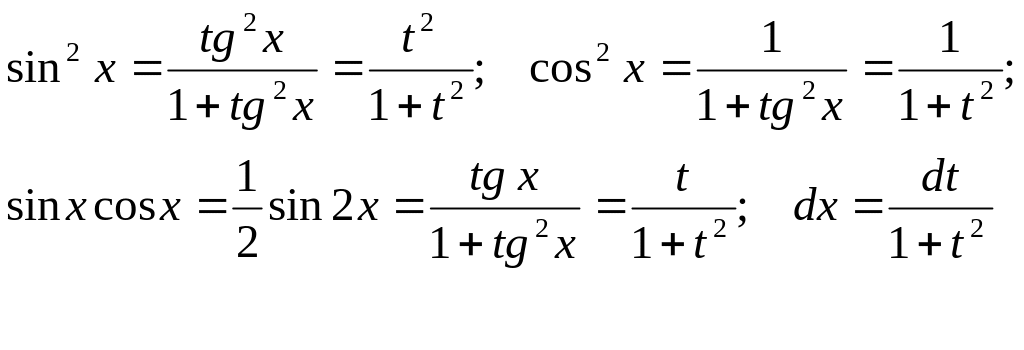в) Интегралы где - рациональная функция, сводятся к интегралу от рациональной функции переменной заменой или :