Глава VIII достоверность контроля и задачи технической эксплуатации средств измерений

Измерения, проводимые в процессе эксплуатации радиотехнических средств, не являются самоцелью. Они являются важнейшей составной частью операции контроля и основой для принятия решения об исправности или неисправности контролируемого объекта. С этой точки зрения погрешности, неизбежно возникающие при измерениях, являются источником неправильных заключений фактическом состоянии контролируемого объекта. Физика появления таких неправильных заключений иллюстрируется на рис.8.1.

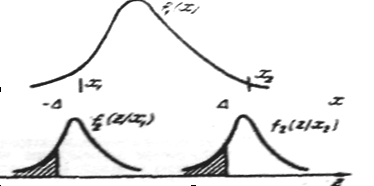
Рис.8.1. Вероятность появления неправильных заключений

по результатам контроля

Пусть контролируется значение некоторого параметра Х описываемого плотностью распределения f₁ (x). Для значений этого параметра из соображении обеспечения эффективности работы объекта не ниже заданного уровня установлена некоторая допусковая область . Если выполняется условие

-  х  , (8.1)

то контролируемый объект считается исправным.

Измерение фактического значения параметра выполняется измерительным прибором, погрешности которого описываются плотностью распределения f2 (у). в первом приближении случайные величины Х и У могут считаться независимыми. Таким образом, вместо истинного значения параметра Х оператор наблюдает случайную величину

Z=X+Y, (8.2)

И условие, по которому фактически оценивается исправность объекта, приобретает вид

-  z  . (8.3)

Разница между условием истинной исправности объекта (8.1) и фактически проверяемым условием (8.3) и обусловливает появление ошибок контроля связанных с погрешностями используемой измерительной аппаратуры. Если предположить, что параметр Х принял определенное значение (х₁ или х₂ на рис.8.1), то возможные результаты измерения распределятся вокруг данного измерительного прибора. Таким образом, кривые f₂ (z/х₁) и f₂ (z/х₂) это плотности распределения погрешностей измерительного прибора при условии, что измеряемый параметр принял значение х₁ или х₂ соответственно.

Как следует из рисунка, в зависимости от конкретного результата измерения возможны следующие ситуации:

Н₁ – показания прибора в пределах допуска и истинное значение параметра в пределах допуска -  х  , -  z  ;

Н₂ – показания прибора за пределами допуска и истинное значение параметра за пределами допуска  < z <-,  < х < -;

Н₃ – показания прибора за пределами допуска, истинное значение параметра в пределах допуска  < z <-, -  х  ;

Н₄ – показания прибора в пределах допуска, истинное значение параметра за пределами допуска -  z  ,  < х < -.

Эта ситуации образуют полную группу несовместимых событий, для которой, как известно

Р (Н₁) + Р (Н₂) + Р (Н₃) + Р (Н₄) =1 (8.4);

Правильное заключение о состоянии контролируемого объекта выдается только в первом и во втором случаях, откуда вероятность принятия правильного решения, называемая достоверностью контроля, определяется как

Р₀=(Н₁)+Р(Н₂) (8.5);

Достоверность является одной из важнейших характеристик процесса контроля, поскольку правильность принимаемых решений определяет в конечном счете эффективность обслуживаемых объектов. Как следует из рис.8.1, величина достоверности зависит от вида плотности распределения контролируемого параметра f₁ (x) положения границ допуска и вида  на оси х относительно f₁ (x) и вида плотности распределения погрешностей измерительного прибора f₂ (у).

Ситуации Н₃ и Н₄ соответствуют ошибочным заключениям по результатам контроля. Ситуация Н₃ отвечает такому случаю, когда неисправность признается фактически исправный объект. Такие ошибки называются ошибками первого рода , а условная вероятность их появления обозначается буквой . На рис.8.1 эта вероятность соответствует заштрихованной площади плотности распределения f₂ (z/х₁). При эксплуатации объектов ошибки первого рода приводят к необходимости проведения дополнительных проверок и ремонтно-регулировочных работ. В результате снижается коэффициент готовности обслуживаемой техники.

Ситуация Н₄ возникает в тех случаях, когда ошибочно признается исправным фактически неисправный объект. Эти ошибки называются ошибками второго рода. Условная вероятность их появления обозначается буквой . На рис.8.1 эта вероятность, соответствуют заштрихованной площади плотности распределения f₂ (z/х₂). Ошибки второго рода приводят к тому, что к выполнению задачи допускаются неисправные объекты, фактически неспособные ее выполнить. Такие ошибки при эксплуатации техники могут привести к катастрофическим последствиям.

Следует отметить, что характеристика достоверности результатов контроля с помощью вероятности Р₀ и с помощью вероятностей ошибок первого и второго рода в вероятностном смысле равноценны, поскольку, как следует из выражения (8.4)

Р₀=1- (+) (8.6);

Однако на практике существенную роль играют не только сами значения вероятностей этих ошибок, но и материальные потери, сопутствующие им. Необходимость учета этих их потерь приводит к тому, что в каждом конкретном случае тот или иной показатель достоверности оказыва­ется, более предпочтительным. Так, в тех случаях, когда потери можно не учитывать вообще или нас интересует только их суммарная величина, более удобным оказывается характеристика достоверности контроля с помощью вероятности Р₀. Однако в большинстве случаев, потери, возникающие в результате ошибок первого и второго рода, существенно неравноценны. Это приводит к необходимости учитывать ошибки первою и второго рода в отдельности и более удобным, оказывается характеризовать достоверность контроля двумя характеристиками — вероятностями ошибок первого и второго рода  и .

Вне зависимости от выбранной системы характеристик, из всего из­ложенного можно сделать вывод, что одной из важнейших задач, воз­никающих при эксплуатации измерительных приборов, является пра­вильный выбор необходимых точностных характеристик приборов, в за­висимости от требований, предъявляемых к достоверности контроля. Может показаться, что наиболее рациональным путем решения задачи является выбор возможно более точного прибора. Однако повышение точности, как правило, сопровождается ростом стоимости и сложности эксплуатации и поэтому не всегда является оправданным.

Точностные свойства прибора характеризуются пределом его допускаемой погрешности (классом точности). Поэтому задача обеспечения заданной достоверности контроля может быть сведена к выбору необходимого класса точности прибора. Однако этим содержание технической эксплуатации измерительной аппаратуры не исчерпывается. Дело в том, что точностные характеристики приборов со временем изменяются. Процессы износа и старения, протекающие во всех узлах и элементах измерительной аппаратуры под влиянием таких факторов, как электрические и механические нагрузки, изменение условий окружающей среды и т.п., приводят к тому, что погрешности приборов случайным образом изменяются (возрастают) во времени и приборы перестают соответствовать своему классу точности.

Отсюда возникает следующая задача технической эксплуатации из­мерительной аппаратуры: проведение мероприятий, обеспечивающих поддержание метрологических свойств приборов во времени в пределах соответствующих норм. Эта задача является частью общегосударственной работы обеспечения единства измерений и единообразия средств измерений, решаемой метрологической службой. Одним из основных мероприятий, проводимых этой службой, является периодическая проверка средств измерений, заключающаяся в периодическом определении метрологическим органом погрешностей средства измерений и установлении его пригодности к применению. Эффективность этого мероприятия в значительной мере определяется тем, насколько правильно установлена периодичность проверки. Действительно, при слишком частых проверках возрастают затраты на их проведение и увеличивается время, в течении которого приборы не используются по прямому назначению. Если же интервалы между проверками велики, то снижается достоверность контроля. Поэтому правильный выбор межпроверочных интервалов является одним из важных факторов организации обслуживания приборов.

ОПРЕДЕЛЕНИЕ НЕОБХОДИМОЙ ТОЧНОСТИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ, ИСПОЛЬЗУЕМЫХ ДЛЯ ДОПУСКОВОГО КОНТРОЛЯ

Сравнение измеренного значения параметра с установленными на него допусками является основним методом решения задачи о пригодности контролируемого обьекта к эксплуатации. Отсюда ясна важность количественного определения требований к точности измерительных приборов, используемых при допусковом контроле. Эта задача может быть сформулирована следующим образом. Пусть для контролируемого параметра х определена допусковая область , а его распределение характеризуется среднеквадратическим отклонением от номинала σ_х. Аналогично пусть измерительный прибор обладает среднеквадратической погрешносью σ_у а через  = 3 σ_у определяется доверительная погрешность измерения. Требуется определить величину - / σ_х при одном из последующих условий:

задана вероятность ошибок первого рода ;

задана вероятность ошибок второго рода ;

задана требуемая достоверность Р₀.

В подобной постановке задача впервые сформулирована и решена професором Н.А. Бородачевым, получившим вираження для вероятностей ошибок  и . Методика вывода может быть пояснена с помощью рис. 8.1. Получим выражение для вероятности ошибок второго рода . Как следует из предшествующих рассуждений, эти ошибки возникают при совместном появлении двух событий: х < — , >х; (8.7)

-<z <.

Последнее неравенство может быть переписано в виде:

-  х+у  ,

откуда следует, что при любом значении х второе событие может появится только в том случае, если для погрешностей измерений выполняется условие -(+х)у-х. (8.8)

Если полагать, что случайные величины X и Y независимы, т.е. что плотность распределения f₂(y) не меняется в зависимости от значения х, то вероятность события (8.8) определится как

.

В то же время вероятность попадания значения х в интервал [х, \ х+dx] определяется как f₁(х)dx. Тогда, с учетом предположения о неза­висимости X и Y, вероятность появления ошибки второго рода при данном значении х определится как

. (8.9)

Теперь, для того чтобы получить значение вероятности Р, достаточно усреднить выражение (8.8) по всем возможным значениям х в интервале, соответствующем первому неравенству (8.7). Тогда окончательно

(8.10)

Аналогично могут быть получены выражения и для остальных ха­рактеристик достоверности контроля, однако, как было показано выше, вероятность ошибок, второго рода представляет наиболее важную характеристику объектов, почему она и рассматривается наиболее подробно. Следует только подчеркнуть, что определение требований к точности прибора по заданной, вероятности ошибок второго рода ,  однозначно определяет и вероятность ошибок первого рода .

Выражение позволяет получить значение вероятности ошибки второго рода при наличии конкретных выражений для законов распределения параметра и погрешности его измерения. Однако непосредственное использование в практических целях слишком сложно, особенно если учесть, что в наиболее распространенных случаях интегралы такого вида не выражаются через элементарные функции. По этому на практике получил распространение графоаналитический метод расчета, когда необходимые характеристики определяются по заранее рассчитанным графикам. Для случая, когда параметр и погрешности измерений распределены по нормальному закону, графики привечены на рисунках.

На рис. 8.2 изображена зависимость требующейся относительной точности измерений / σ_х от заданной величины вероятности ошибок второго рода  при различных соотношениях между допуском на параметр  и величиной его среднеквадратичного отклонения σ_х . На рис. 8.3 изображена зависимость между относительной точностью измерений и вероятностью ошибки первого рода  при тех же условиях.

Для того чтобы пояснить методику пользования этими графиками, рассмотрим процесс решения наиболее часто встречающейся на практике задачи. Имеется некоторый параметр Х, распределенный по нормальному закону со среднеквадратическим отклонением σ_х. Допуск на параметр составляет  = 2 σ_х . требуется определить такой допуск на погрешности измерительного прибора, чтобы выполнялось условие 0,01, и оценить вероятность возникновения при этом ошибок первого рода.

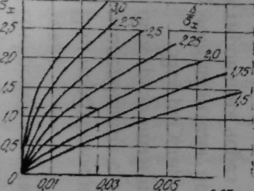
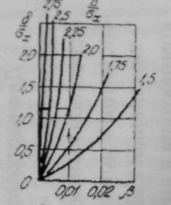
Рис.8.2 Номограмма Рис.8.3 Номограмма для

для определения определения требований к

требований к точности прибора точности прибора по заданной вероятности по заданной вероятности ошибки второго рода β. ошибки первого рода α.

Для решения задачи на рис.8.2. проводим пунктирную линию из точки =0,01 до пересечения с кривой  / σ_х=2,0 и на вертикальной оси определяем требования к прибору  / σ_х=1,15. Далее на рис.8.3 из точки  / σ_х=1,15 проводим линию до пресечения с кривой  / σ_х=2,0. Из точки пересечения опускаем перпендикуляр на ось абсцисс и получаем, что при данных условиях вероятность ошибки первого рода составит =0,026. По известным  и  может быть определена и достоверность контроля

Р₀=1- (+)= 0,964.