Глава VII измерение вероятностных характеристик случайных процессов
Особенности измерения:
Сложность классификации (выбора модели случайного процесса: эргодичность, стационарность).
Возможность многократного воспроизведения анализируемых реализаций.
Обязательность операции усреднения.
Необходимость иметь большой объем статистического материала
Специфика методов и методик измерения.
Сложность поверки и аттестации.
Основные сведения о вероятностных характеристиках
Наиболее
полная характеристика случайного
процесса
- n-мерный
закон распределения вероятностей. На
практике используют одномерные законы
распределения:
функции распределения - наиболее полная характеристика (для дискретных и непрерывных величин), определяет вероятность того, что случайный процесс будет меньше наперед заданного значения
;плотность распределения
Параметры:
— математическое ожидание (МО)
-
характеризует среднее значение;
— дисперсия (мощность) случайного процесса x(t):
;
—Корреляционный момент
где
f(х,у)
- двумерная
плотность распределения. Для независимых
и
,
тогда
,т.к.
каждый из первых центральных моментов
равен 0:
ВЫВОД!
Если корреляционный момент двух случайных
величин не равен 0, то это признак их
зависимости друг от друга,
характеризует
не только степень зависимости между
величинами х
и
у, но и степень
их рассеивания относительно среднего
значения. Поэтому для характеристики
связи в чистом виде переходят к
коэффициенту корреляции:
;
пределы изменения
:
,
где
среднеквадратические
отклонения x(t)
и
.
Измерение параметров случайных процессов.
Ограничения: x(t) - стационарный, эргодический случайный процесс. Математическое ожидание (МО.) оценивается по одной реализации x(t) в соответствии с алгоритмом (аналоговое измерение):
*
- оценка М.О. x(t)
на интервале (0-Т);
,
где
-максимальное
время корреляции процесса x(t).
(рис.9.1)
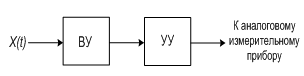
Рис. 7.1
УУ – усредняющее устройство.
Структурная схема аналогового измерителя мо.
Основной узел структурной схемы — "идеальный" интегратор (RC-цепь, магнитоэлектрический прибор, интегратор на базе усилителя с глубокой отрицательной связно).
У
идеального интегратора 
При цифровом измерении М.О. (рис.7.2)
-
отсчеты x(t),
взятые через интервал
;
N - общее число отсчетов
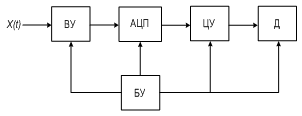
Рис. 7.2 Структурная схема цифрового измерителя М.О.
На схеме указаны:
ЦУ – цифровой усреднитель;
БУ – блок управления.
Условие
выбора
,
где
-
максимальное значение интервала
корреляции.
При
этом
-
дисперсия оценки М.О.
Dx - дисперсия исследуемого процесса.
Алгоритм оценки М.О. неудобен, т.к. требует наличие ЗУ с большой памятью: выдача результата измерения М.О. с задержкой во времени на величину N плюс время на усреднения результатов измерения. Предлагается в качестве алгоритма оценки М.О. рекуррентное соотношение:
-
текущая оценка
на i-ом
шаге (по i
отсчетам).
* - означает оценку результата измерений.
Рекуррентная формула позволяет шаг за шагом (в темпе поступления отсчетов) определить любой i-й член последовательности, если известен результат измерения по (i-1) отсчетам.
Кроме измерительной части в приборах есть интерфейсная часть. Стандарты на интерфейс (МЭК, КАМАК...).