3.2. Задания

1. Для изготовления четырех видов продукции (П1, П2, ПЗ, П4) используются три вида ресурсов (P1, P2, Р3). Другие условия представлены в следующей таблице:

Ресурсы	Запас ресурсов, ед.	Нормы расхода сырья на единицу продукции, ед.
		П1	П2	П3	П4
Р1	3500	2	1	1	4
Р2	1300	1	5	3	0
Р3	3200	3	0	6	2
Прибыль от единицы продукции, ден.ед.		9	4	6	15

Необходимо определить план выпуска продукции, при котором прибыль от ее реализации будет максимальной.

2. Для изготовления семи видов продукции (П1, П2, ПЗ, П4, П5, П6, П7) используются пять видов ресурсов (Р1, Р2, РЗ, Р4, Р5). Другие условия представлены в следующей таблице:

Ресурсы	Запас ресурсов, ед.	Нормы расхода сырья на единицу продукции, ед.
		П1	П2	П3	П4	П5	П6	П7
Р1	1500	2	1	1	4	4	4	3
Р2	3100	1	5	3	0	0	2	0
Р3	2300	5	5	1	2	4	2	0
Р4	1000	3	0	1	6	0	2	2
Р5	4500	1	5	6	2	7	9	2
Прибыль от единицы продукции, ден.ед.		20	10	3	4	11	15	23

Необходимо определить план выпуска продукции, при котором прибыль от ее реализации будет максимальной.

3.3. Контрольные вопросы

1. Опишите сущность задачи линейного программирования.

2. Математическая форма записи задачи линейного программирования.

3. Как математическая форма записи связывается с шаблоном для решения задачи линейного программирования?

4. Каким образом производится поиск решения задачи линейного программирования?

5. О чем говорят результаты расчета в случае успешного поиска оптимального значения?

6. Как минимизировать целевую функцию средствами Excel при заданной системе ограничений?

Лабораторная работа № 4 Задачи оптимальных перевозок

Цель работы: – освоить решение задач оптимальных перевозок с помощью MS Excel;

– получить навыки использования транспортных задач в хозяйственной деятельности современных предприятий и организаций.

4.1. Основные сведения

Общая постановка задачи оптимальных перевозок (транспортной задачи) состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А₁, А₂, ..., А_m в п пунктов назначения В₁, В₂, ..., В_n.

В качестве критерия оптимальности (целевая функция) обычно задается минимальная суммарная стоимость перевозок всего груза или минимальная суммарная транспортная работа по доставке грузов, которая может быть пропорциональна времени доставки грузов потребителям или расстоянию между поставщиками и потребителями. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная суммарная стоимость перевозок всего груза [3, 5, 6].

Обозначим с_ij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через a_i – запасы груза в i-ом пункте отправления, через b_j – потребности в грузе в j-ом пункте назначения, а через x_ij – количество единиц груза, перевозимого из i-ro пункта отправления в j-й пункт назначения. Тогда математическая модель транспортной задачи состоит в определении минимального значения функции:

при условиях

Поскольку переменные удовлетворяют системам линейных уравнений и условию неотрицательности (4.2), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз всего имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Суммарное количество груза у поставщиков равно , а суммарная потребность в грузе в пунктах назначения равна единиц. Если суммарная потребность в грузе в пунктах назначения равна суммарному запасу груза в пунктах отправления, т. е.

то такая транспортная задача называется закрытой или сбалансированной. В противном случае – открытой или несбалансированной.

В случае превышения суммарного запаса над суммарной потребно­стью, т. е. если

вводится фиктивный n+1-й потребитель (или пункт назначения) с потребностью, равной:

а соответствующие транспортные тарифы от всех поставщиков до фиктивного потребителя полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (4.3).

В случае превышения суммарной потребности в грузе над суммарными запасами поставщиков, т. е. если

вводится фиктивный m+1-й пункт отправления с запасом груза в нем, равным:

а соответствующие транспортные тарифы от фиктивного поставщика до всех потребителей полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (4.3).

Замечания.

1. Перед решением транспортной задачи необходимо сначала проверить, является ли транспортная задача открытой или закрытой. Если транспортная задача является открытой, то необходимо ввести фиктивного поставщика или фиктивного потребителя.

2. Оптимальное решение транспортной задачи при целочисленных правых частях ограничений всегда является целочисленным.

3. В целевой функции коэффициенты c_ij могут быть как тарифами, так и расстояниями между пунктами отправления и получения грузов или временами доставки грузов. В двух последних случаях целевая функция представляет собой транспортную работу.

Рассмотрим решение транспортной задача на следующем примере.

Предположим необходимо организовать поставки сырья на 5 заводов города Владикавказ. На заводах спрос на сырье равен соответственно 500 ед., 600 ед., 500 ед., 5000 ед. и 1000 ед. Сырье сосредоточено у четырех поставщиков на складах в разных городах, запасы которых равны 750 ед., 900 ед. 4500 ед. и 550 ед. Сырье на заводы может завозиться от любого поставщика. Стоимость перевозки единицы сырья c_ij (i – номер поставщика, j – номер завода-потребителя) известны и задаются матрицей:

Составить такой план перевозок, при котором суммарная стоимость всех перевозок будет минимальной.

Математическая модель. Обозначим через х_ij количество единиц сырья, перевозимого от i-гo поставщика на j-й завод. Так как сумма запасов грузов 750+ 900 + 4500 + 550 = 6700 поставщиков не равна сумме потребностей грузов потребителей: 500 + 600 + 500 + 5000 + 1000 = 7600. Таким образом, потребности в грузах у потребителей превышают их запасы у поставщиков и данная транспортная задача является открытой. Для того чтобы она стала закрытой, вводим фиктивного поставщика с номером 5, у которого запас груза равен 7600– 6700 = 900 ед. В этом случае суммарный запас у поставщиков станет равным 7600 и мы получим закрытую транспортную задачу. При этом все тарифы от фиктивного поставщика ко всем потребителям груза полагаются равными нулю. В матрице тарифов появится пятая строка, в которой стоят все нули:

Условия доставки необходимого сырья и вывоза имеющегося сырья обеспечиваются выполнением следующих равенств-ограничений:

Целевая функция, выражающая суммарную стоимость перевозок, при данном плане составит:

Таким образом, математическая постановка задачи состоит в нахождении такого неотрицательного решения системы линейных равенств-ограничений (4.4) и (4.5), при котором целевая функция (4.6) принимает минимальное значение.

Решение задачи средствами Excel.

Создаем рабочую форму на чистом листе книги Excel (рис. 4.1).

Рис. 4.1. Созданные рабочей формы для решения транспортной задачи.

В ячейках B4:B8 заносим запасы грузов, хранящиеся на складах у поставщиков, включая и фиктивного поставщика, в ячейках E4:E8 заносим потребности в сырье на заводах. В ячейки с адресами B15:F19 занесены коэффициенты матрицы стоимости на перевозку сырья между всеми пунктами отправления и назначения. Пятая строка этой матрицы соответствует (ячейки B19:F19) перевозкам от фиктивного поставщика.

В ячейки G26:G30 введем формулы для расчета ограничений (4.4), а в ячейки B31:F31 – формулы для расчета ограничений (4.5).

Формулу для расчета целевой функции вводим в ячейку I21 и имеет следующий вид:

=СУММПРОИЗВ(B15:F19;B26:F30).

Выполним команду Сервис→Поиск решения... Откроется диалоговое окно Поиск решения. В поле Установить целевую ячейку необходимо указать $I$21. Установить переключатель Равной: минимальному значению, что означает минимизацию значения целевой функции.

В поле Изменяя ячейки указать диапазон ячеек, в которые необходимо будет поместить значения объемов производства для каждого вида продукции, т.е. необходимо указать диапазон $B$26:$F$30.

В поле Ограничения: вводим ограничения для расчета, для чего необходимо нажать кнопку Добавить и в появившемся диалоговом окне заполнить ограничения для каждого равенства ($B$31:$F$31=$E$4:$E$8, $G$26:$G$30=$B$4:$B$8, $B$26:$F$30=целое и $B$26:$F$30>=0). Диалоговое окно Поиск решения будет выглядеть, как на рис. 4.2.

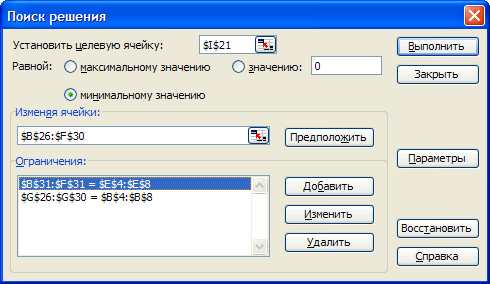
Рис. 4.2. Диалоговое окно Поиск решения с занесенными данными.

В диалоговом окне Поиск решения нажимаем кнопку Выполнить. Если оптимальное решение существует, на экран будет выведен следующий диалог, свидетельствующий об успешном поиске оптимального решения.

Предложенное Сохранить найденное значение означает, что найденные оптимальные значения по стоимости перевозок в заданной системе ограничений, минимзирующие целевую функцию будут помещены в соответствующие ячейки $B$26:$F$30.

Восстановить исходные значения – означает отмену проведенного расчета. Если решение найти не удалось, то пользователю будет выведен диалог о неуспешной попытке поиска оптимального решения.

Результат расчета представлен на следующем рис. 4.3. Из рисунка видно, что суммарная минимальная стоимость всех перевозок составит 15050 денежных единиц.

Рис. 4.3. Результат решения транспортной задачи.

Полученный результат позволяет сделать вывод, что сырье от Поставщика 1 надо вести сырье на Завод 1 (х₁₁) в количестве 194 ед., на Завод 2 (х₁₂) – 506 ед. и на Завод 3 (х₁₃) – 50 ед. От Поставщика 2 надо вести сырье на Завод 1 (х₂₁) в количестве 306 ед., на Завод 2 (х₂₂) – 94 ед. и на Завод 4 (х₂₄) – 500 ед. Поставщик 3 все сырье отправляет на Завод 4 (х₃₄) – 4500 ед. Поставщик 4 все сырье отправляет на Завод 5 (х₄₅) – 550 ед. От фиктивного Поставщика 5 на Завод 3 (х₅₃) в количестве 450 ед. и на Завод 5 (х₅₅) – 450 ед.

Переменные х₁₄ = х₁₅ = х₂₃ = х₂₅ = х₃₁ = х₃₂ = х₃₃ = х₃₅ = х₄₁ = х₄₂ = х₄₃ = =х₄₄ = х₅₁ = х₅₂ = х₅₄.