1.4. Примеры решения задач с использованием финансовых функций Exсel
Вычислить значение суммы на расчетном счете по истечении 6 лет, если в банке размещено 10000 р. под 10% годовых и начисление процентов производится один раз в год.
Запускаем приложение Excel, в строке формул нажимаем кнопку fx или выбираем команду Вставка→Функция, откроется диалоговое окно Мастер функции. В раскрывающем списке категория выбираем Финансовые, а в списке функции функцию БС и в открывшемся диалоговом окне вводим аргументы функции, как показано на рис. 1.1.
Ответ: БС(ставка;кпер;плт;пс;тип)=БС(10%;6;;-10000)=17715р61к.
Условия те же, но начисление процентов производится раз в полгода (см. рис. 1.2).
Ответ: БС(ставка;кпер;плт;пс;тип)=БС(10%/2;6*2;;-10000)=17958р56к.
Вычислить значение суммы на расчетном счете по истечении 3 лет, если вкладчик в конце каждого месяца перечисляет сумму в 500р. под 10% годовых (рис. 1.3).
Ответ: БС(ставка;кпер;плт;пс;тип)=БС(10%/12;3*12;-500)=20890р91к.
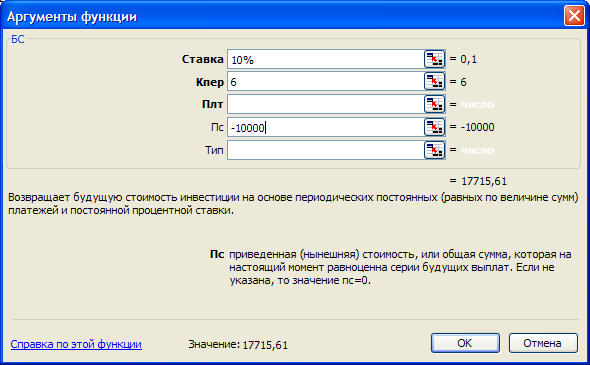
Рис. 1.1. |
Ввод аргументов функции БС. |
Рис. 1.2. Ввод аргументов функции БС.
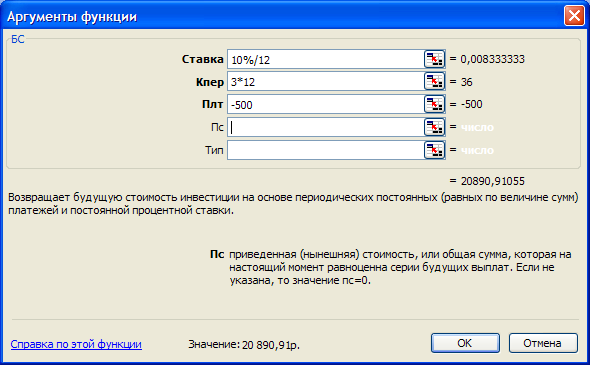
Рис. 1.3. Ввод аргументов функции БС.
Условия те же, но в начале месяца:
Ответ: БС(ставка;кпер;плт;пс;тип)=БС(10%/12;3*12;-500;;1)=21065р00к.
К примеру мы хотим накопить 20000р. за 5лет, положив некоторую сумму в банк при условии начисления 14% годовых ежегодно. Найти эту первоначальную сумму (рис.1.4).
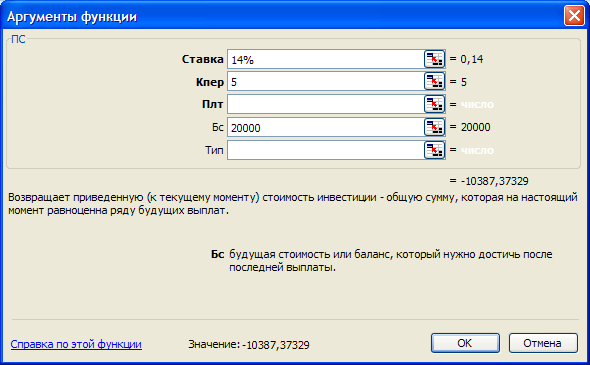
Рис. 1.4. Ввод аргументов функции ПС.
Ответ: ПС(ставка;кпер;плт;бс;тип)=ПС(14;5;;20000)=-10387р37к.
Проведем проверку: БС(14%;5;;-10387,37)=20000р., таким образом значениесовпало с аргументом бс функции ПС.
Найти ежемесячную выплату по четырехгодичному займу в 10000р., выданному под 12% годовых (рис. 1.5).
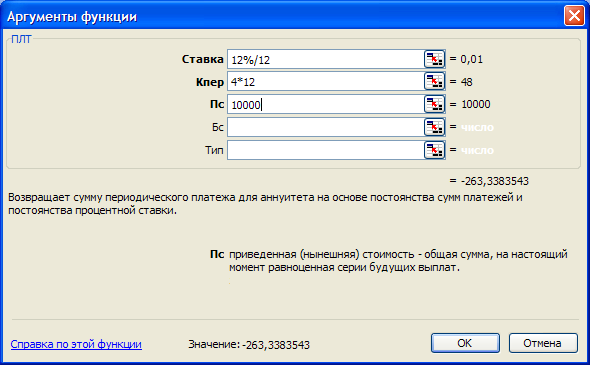
Рис. 1.5. Ввод аргументов функции ПЛТ.
Ответ: ПЛТ(ставка ;кпер;пс;бс;тип)=ПЛТ(12%/12;4*12;10000)=-263р34к.
Рассчитать размер периодического ежемесячного платежа кредита размером 300000р., выданного на 3 года, с процентной ставкой 6% годовых.
Ответ: ПЛТ(ставка ;кпер;пс;бс;тип)=ПЛТ(6%/12;3*12;300000)=-9126р58.
Рассмотрим обратную задачу. Рассчитать количество периодов выплаты 6%-го кредита, размером 300т.р. с ежемесячной выплатой –9126,58 р. Для решения используем функцию КПЕР (рис 1.6).
Рис. 1.6. Ввод аргументов функции КПЕР.
КПЕР(ставка ;плт;пс;бс;тип)=КПЕР(6%/12;-9126,58;300000)=36.
Ответ: Количество периодов выплат составит 36 месяцев или 3 года.
Отсюда следует, что функция КПЕР обратно функции ПЛТ.
Определить процентную ставку для 3-летнего займа в 20000р. с ежемесячной выплатой в 600р. Решение задачи показано на рис. 1.7.
Рис. 1.7. Ввод аргументов функции СТАВКА.
СТАВКА(кпер;плт;пс;бс;тип;предположение)=СТАВКА(3*12;-600;20000)= =0,42%, т.к. это месячная процентная ставка, то годовая процентная ставка составит 0,42*12=5,06%.
Ответ: Годовая процентная ставка составит 5,06%.
Выполнить расчет 10-летней ипотечной ссуды покупки квартиры за 1200000р. с годовой ставкой 13% и начальным взносом 30%. Сделать расчет ежегодных и ежемесячных выплат.
Для решения данной задачи необходимо использовать функцию ПЛТ. Решение данной задачи показано на рис. 1.8 и рис. 1.9. На рис. 1.8 указаны необходимые формулы для решения задачи, а на рис.1.9 – полученные результаты.
Рис. 1.8. Формулы для решения задачи.
Рис. 1.9. Результаты расчета.