3.5. Задания

1. Сформировать последовательность случайных чисел, имеющую равномерное распределение в интервале от 0 до 1, построить гистограмму и получить описательную статистику.

2. Сформировать последовательность случайных чисел, распределенную по закону Бернулли, если р = 0,27, построить гистограмму и получить описательную статистику.

3. Сформировать последовательность случайных чисел, распределенную по биномиальному закону, если р = 0,2 и число испытаний равно 2, построить гистограмму и получить описательную статистику.

4. Сформировать последовательность случайных чисел, распределенную по закону Пуассона, при λ = 10, построить гистограмму и получить описательную статистику.

5. Сформировать модельное распределение для формирования последовательности: 1, 1, 4, 4, 7, 7, 10, 10, 1, 1, 4, 4, 7, 7, 10, 10.

6. Построить скользящее среднее для данных о спросе на товар по месяцам по трем и четырем точкам. Исходные данные и результаты представлены на рис. 3.7–3.9.

Итоговые данные		Полученные результаты
месяц	спрос	по трем точкам	по четырем точкам
Январь	4039	#Н/Д	#Н/Д
Февраль	4057	#Н/Д	#Н/Д
Март	4052	4049,333333	#Н/Д
Апрель	4094	4067,666667	4060,5
Май	4104	4083,333333	4076,75
Июнь	4110	4102,666667	4090
Июль	4154	4122,666667	4115,5
Август	4181	4148,333333	4137,25
Сентябрь	4185	4173,333333	4157,5
Октябрь	4195	4187	4178,75
Ноябрь	4229	4203	4197,5
Декабрь	4244	4222,666667	4213,25
Январь	4242	4238,333333	4227,5
Февраль	4283	4256,333333	4249,5
Март	4298	4274,333333	4266,75

Рис. 3.7. Исходные данные и полученные результаты.

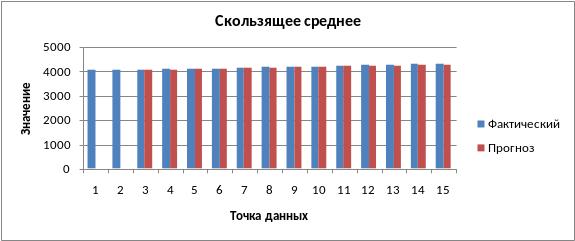
Рис. 3.8. Скользящее среднее для данных о спросе

по месяцам на товар по трем точкам.

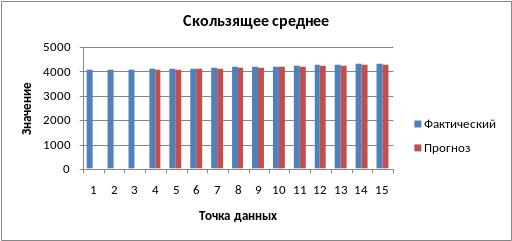
Рис. 3.9. Скользящее среднее для данных о спросе

по месяцам на товар по четырем точкам.

3.6. Контрольные вопросы

1. Для чего используется метод корреляционно-регрессионного анализа?

2. Что представляет собой коэффициент корреляции? Опишите уравнение для коэффициента корреляции.

3. Какие показатели используются для характеристики изменчивости признаков? Дайте их определения.

4. Дайте характеристику тесноты связи в зависимости от величины коэффициента корреляции.

5. В чем заключается линейный регрессионный анализ, для чего используется регрессия? Какой вид имеет линейное уравнение регрессии?

6. Что характеризуют коэффициенты регрессии и по каким формулам они вычисляются?

7. Какие графики могут быть построены при проведении корреляционно-регрессионного анализа?

8. По каким данным строится уравнение регрессии и что оно означает? Какие результаты отражаются при выводе итогов регрессионного анализа помимо коэффициентов?