3.4. Примеры решения задач

Пример 1. Рассчитать коэффициент корреляции, характеризующий тесноту связи между величиной оптово-складского товарооборота и размером складской площади фирмы. Значения элементов X (складская площадь) и Y (оптово-складской товарооборот) указаны в табл. 3.2.

Таблица 3.2

Наименование организации	Складская площадь, кв.м., Х	Оптово-складской товарооборот, руб., Y
Фирма 1	4286	1270138
Фирма 2	6845	520466
Фирма 3	2910	135968
Фирма 4	1156	305454

Решение:

Введем исходные данные как показано на рис. 3.1. Для расчета коэффициента корреляции, с помощью Мастера функций из категории Статистические выбираем функцию КОРРЕЛ. В диалоговом окне функции указываются массивы Складской площади и Оптово-складского товарооборота. В ячейке В6 отображается формула для получения результата =КОРРЕЛ(В2:В5;С2:С5).

Ответ:=0,353990796.

Пример 2. На основе данных предыдущего задания выполнить регрессионный анализ.

Решение: Выполним команду Данные→Анализ данных→Регрессия. Откроется диалоговое окно Регрессия. Убедитесь, что в диалоговом окне Надстройки (Кнопка «Office»→Параметры Excel→Надстройки→Перейти…) установлен флажок Пакет анализа. Вводим входные данные диапазонов значений X и Y в диалоговом окне Регрессия. В строке Уровень надежности установите флажок (по умолчанию уровень надежности составляет 95%). В поле Параметры вывода укажите Новый рабочий лист (рис. 3.2).

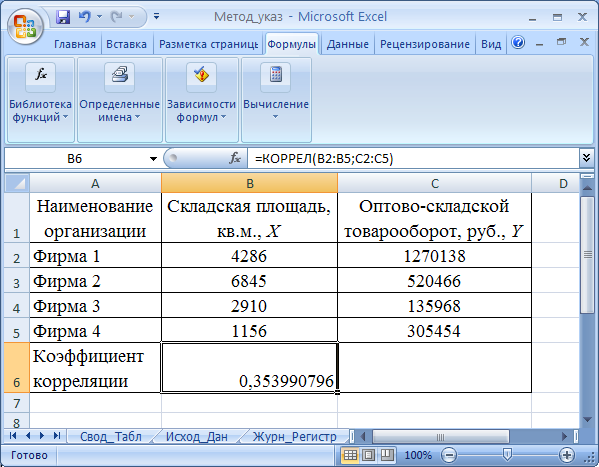
Рис. 3.1. Исходные данные и результат расчета коэффициента корреляции.

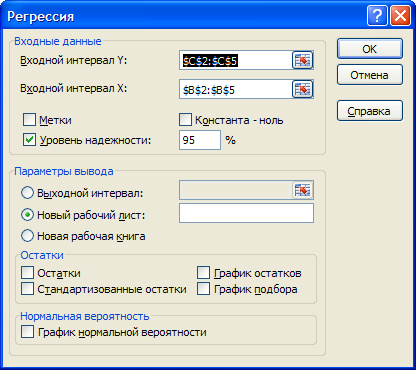
Рис. 3.2. Диалоговое окно Регрессия.

Результаты регрессионного анализа выводятся на экран в заданные ячейки (вывод итогов, рис. 3.3). Уравнение регрессии строится по данным, указанным в графе Коэффициенты. Строка Y-пересечение показывает значение свободного члена 277828,56; строка Переменная Х1 – значение переменной при Х1=73,74. Уравнение регрессии имеет вид: у = 277826,56 + 73,74х. Это однофакторная модель.

Рис. 3.3. Вывод итогов корреляционно-регрессионного анализа.

Пример 3. Сформировать последовательность случайных чисел, распределенную по нормальному закону со средним значением 0 и стандартным отклонением 1, построить гистограмму и получить описательную статистику.

Решение: На новом рабочем листе выполним команду Данные→Анализ данных→Генерация случайных чисел (рис. 3.4). В диалоговом окне Генерация случайных чисел в поле Число переменных указать 1, Число случайных чисел 100, Распределение – нормальное, Параметры: Среднее=0, Стандартное отклонение=1, Параметры вывода: Выходной интервал – А1. В результате будет сгенерирована последовательность случайных чисел.

Для построения гистограммы:

• введем в ячейки В1:В7 границы частотных интервалов от -3 до 3 с шагом 1 – это будет карман;

• выполним команду Данные→Анализ данных→Гистограмма;

• в диалоговом окне Гистограмма укажем: в поле Входной интервал – А1:А100, Интервал карманов – В1:В7, Выходной интервал – С1, установим флажок Вывод графика;

• в результате будет построена гистограмма (рис. 3.5).

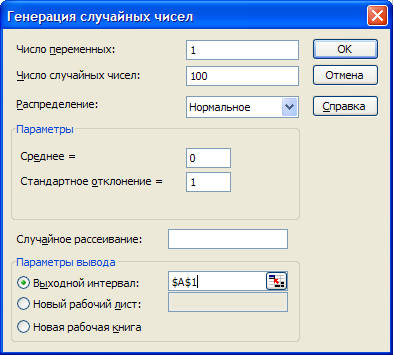
Рис. 3.4. Диалоговое окно Генерация случайных чисел.

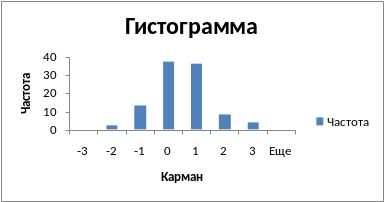
Рис. 3.5. Гистограмма частот.

Для получения описательной статистики выполним команду Данные→Анализ данных→Описательная статистика, в поле Входной интервал укажем А1:А100, Группирование – по столбцам, Выходной интервал – адрес ближайшей свободной ячейки, установите флажок Итоговая статистика, Уровень надежности – 95%. В результате будет получена таблица основных статистических характеристик для заданного множества исходных данных (рис. 3.6).

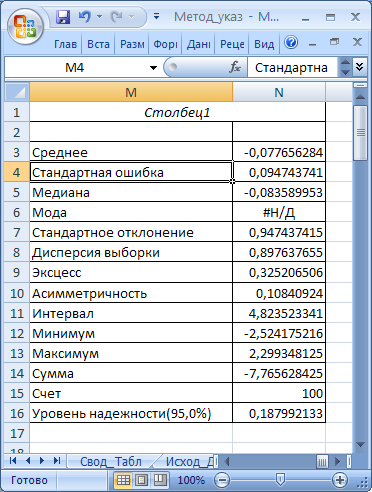
Рис. 3.6. Таблица основных статистических характеристик.