2.5. Адаптивные методы в прогнозировании

При обработке временных рядов наиболее ценной является ин­формация последнего периода, так как необходимо знать, как будет развиваться тенденция, существующая в данный момент, а не тен­денция, сложившаяся в среднем на всем рассматриваемом периоде. Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, степень устаревания данных Адаптивными называются методы прогнозирования, позволяющие строить самокорректирующиеся экономико-математические модели, которые способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда. Благодаря указанным свойствам адаптивные методы особенно удачно используются при краткосрочном прогнозировании. Схема построения моделей прогнозирования приведена на рис. 2.6.

Рис. 2.6. Схема построения адаптивных моделей

Обозначения, приведенные на рис. 2.6:

y(t) - фактические уровни временного ряда;

- прогноз, сделанный в Момент времени t на r единиц времени (шагов) вперед;

— ошибка прогноза, полученная как разница между фактическим и прогноз­ным значением показателя в точке (t +1).

Рассмотрим некоторые методы адаптивного прогнозирования.

Экспоненциальное сглаживание применяется с использованием рекуррентной формулы

где — значение экспоненциальной средней в момент времени t;

α—параметр сглаживания, 0 < α< 1; β = l- α.

Если последовательно использовать формулу (2.13), то экспо­ненциальную среднюю можно выразить через предшествующее значение уровней временного ряда. При

Таким образом, величина оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции.

Например, пусть α = 0,3. Тогда вес текущего наблюдения y(t) бу­дет равен α = 0,3, вес предыдущего уровня будет соответство­вать ар = 0,3-0,7 = 0,21; для уровня у,_2 вес составит для уровня вес составит =0,147; ,для вес =0,1029 и т.д.

При использовании экспоненциальной средней для краткосроч­ного прогнозирования предполагается, что модель ряда имеет вид

где — варьирующийся во времени средний уровень ряда; -случайные отклонения.

Прогнозная модель определяется равенством

где — прогноз, сделанный в момент времени t на единиц времени вперед;

—оценка

Параметр модели определяется экспоненциальной средней

Отсюда формулу (2.13) можно представить в виде

Величину можно рассматривать как погрешность прогноза. Тогда новый прогноз получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.

Адаптивные модели сезонных явлений могут быть описаны мо­делями двух типов – с мультипликативными и аддитивными коэффициентами сезонности:

где - характеристика тенденции развития;

—«аддитивный; коэффициент сезонности;

— мультипликативный коэффициент сезонности;

— количество фаз в полном сезонном цикле.

Рассмотрим модель Уинтерса с линейным характером тенденции мультипликативным сезонным эффектом. Эта модель является объединением двухпараметрической модели линейного роста Хольта и сезонной модели Уинтерса, поэтому ее часто называют моде­лью Хольта-Уинтерса.

Прогноз по модели Хольта-Уинтерса на шагов вперед опреде­ляется выражением

Обновление коэффициентов осуществляется по формулам:

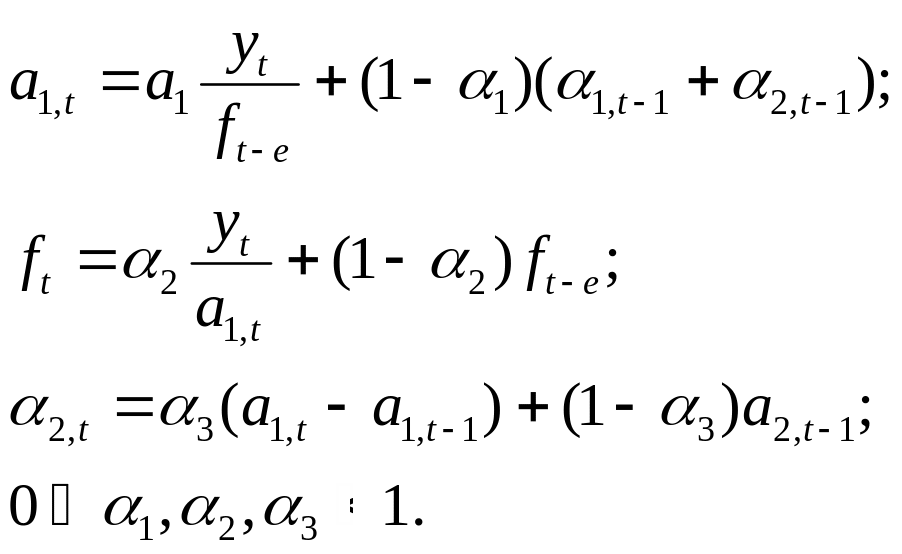
Величина является взвешенной суммой текущей оценки , полученной путем очищения от сезонных колебаний фак­тических данных , и предыдущей оценки.

В качестве коэффициента сезонности берется его наиболее позд­няя оценка, сделанная для аналогичной фазы цикла .

Затем величина используется по первому уравнению для оп­ределения новой оценки коэффициента сезонности по второму уравнению. Оценки модифицируются по процедуре, аналогич­ной экспоненциальному сглаживанию.

Пример. Прогнозирование курса акций осуществлялось на ос­нове адаптивной полиномиальной модели второго порядка:

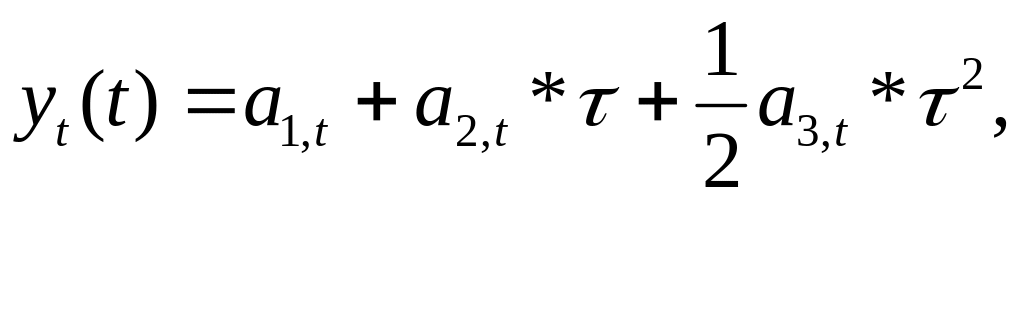
где —период упреждения.

На последнем шаге получены следующие оценки коэффициен­тов: = 541,53;

= -0,41; = -0,72.

Рассчитать прогноз курса акций на один и два дня вперед.

Решение. Прогноз по адаптивной полиномиальной модели второго порядка формируется на последнем шаге путем подста­новки в уравнение модели последних значений коэффициентов и значения - времени упреждения.

При = 1

При = 2