Проверка статистических гипотез
Информация, полученная на основе выборки из некоторой генеральной совокупности может быть использована для предположения относительно некоторых свойств общей генеральной совокупности.
Пусть получена
некоторая оценка
по выборке из N
элемента, которая относится к некоторым
независимым величинам х1,
х2,
х3,
..., хn.
Тогда можно
предположить, что истинное значение
параметра
.
Тогда вполне очевидно, можно предположить,
что от выборки к выборке значение
будет изменяться. Это связано со
статистическою изменчивостью.
Возникает следующий
вопрос — при каком отклонении оценки
от
гипотеза о равенстве должна быть
отвергнута как несостоявшаяся.
Ответ на этот вопрос можно дать, вычислив вероятность любого значимого отклонения от , по выборочному распределению с оценкой .
Если вероятность
такого отклонения мала, то следует
считать отличия истинного параметра и
гипотеза о равенстве
должна отвергаться.
В свою очередь вероятность такого отклонения можно понимать как естественную статистическую изменчивость. И гипотеза о равенстве может быть принята.
Статистическая гипотеза H — некоторое предположение относительно свойств генеральной совокупности, из которых была получена соответствующая выборка.
Параметрические гипотезы – предположения, в которых по выборке наблюдений необходимо проверить параметры распределения.
Проверяемая
параметрическая гипотеза называется
нулевой
гипотезой
и обозначается Н0.
Наряду с гипотезой Н0
рассматривают
одну из альтернативных (конкурирующих)
гипотез
Н1.
Напрмер, если проверяется гипотеза Н0
о равенстве
параметра
, то в качестве
гипотезы Н1
может быть
выбрана одна из гипотез:
.
Выбор
альтернативной гипотезы определяется
конкретно формулировкой задачи.
Правило, по которому принимается решение принять или отклонить гипотезу Н0, называется статистическим критерием К.
В качестве
статистистики
Z критерия К выбирают
ту же статистику, что и для оценки
параметра
, т.е.
Перед
анализом
выборки фиксируется некоторая малая
вероятность
,
называемая уровнем
значимости.
Уровень значимости
— вероятность
использования при проверке соответствующих
статистических гипотез.
Этапы проверки статистических гипотез:
1. Формулируется нулевая (проверяемая) гипотеза Н0 и альтернативная гипотеза Н1;
2. Выбирается статистический критерий К и его статистика Z;
3. Вычисляется наблюдаемое (расcчетное) значение параметра Кнабл., либо здесь вычисляют наблюдаемое (расчетное) значение критерия (статистики Z) при условии, что верна Н0;
4. В зависимости от уровня значимости по соответствующим таблицам находят критическое значения критерия (Ккр.);
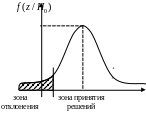
5. Сравнивают наблюдаемое и критическое значение соответствующего критерия (сравнивают статистики), после чего делают вывод относительно соответствующей гипотезы.
Например, если Кнабл. < Ккр., (рис.1)то гипотеза Н0 верна.
Если же Кнабл. > Ккр, (рис.1)— гипотеза Н0 неверна.
и формулировки альтернативной гипотезы Н1
