3.7.4. Неоднородности продуктивных пластов

Физические свойства коллекторов нефти в объеме резервуара (неф­тяного пласта) изменяются в широком диапазоне случайным образом. Они могут изменяться по простиранию пласта и по вертикали. Для характери­стики этих изменений используется аппарат математической статистики и теории вероятности.

Для отображения и учета неоднородности пород строится статисти­ческая модель фильтрационного поля пласта при условии представитель­ности выборки той или другой случайной оставляющей (пористости, про­ницаемости и т.д.).

Исследуемые свойства пласта принимаются за случайные величины с определенной функцией распределения или интегральным законом распределения F(x). Производная от функции распределения называется плотностью распределения:

(3.55)

Чаще эти функции используют для отображения неоднородности пород по проницаемости. Пусть х_ь х₂, х₃...х_п - свойства среды, появляю­щиеся в генеральной совокупности признака с вероятностью Р₁ Р₂ Р₃...Р_n, тогда средневзвешенное значение свойства среды можно вычислить по формуле:

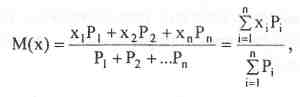(3.56)

Так как имеем

(3.57)

Приняв искомое свойство пород за непрерывную случайную величину, получим:

(3.58)

где f(x)–плотность распределения свойства.

Для конкретных задач можно использовать ряд других показателей распределения, чаще это среднеквадратическое отклонение - σ(х), коэффи­циент вариации

и пр.

В результате изучения какого-либо свойства получают статистиче­ский ряд с заданными исследователем границами разделов (классов). Гра­фически эти результаты отображаются на гистограммах (полигонах рас­пределения):

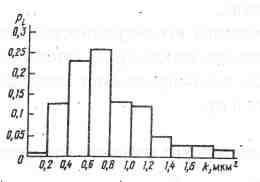
Рис. 3.17. Гистограмма распределения проницаемости

Графическое изображение накопленной частоты встречаемости при­знака представляет собой кумулятивную кривую. При увеличении числа разрядов (уменьшении шага классов) гистограмма приближается к графику плотности распределения случайных величин, а кумулятивная кривая - к функции распределения.

Практически редко достигают по объему выборки условия достаточ­ности генеральной совокупности, поэтому подбираются теоретические главные кривые распределения, наилучшим образом описывающие полу­ченное статистическое распределение (используют специальные коррелляционные методы). Теоретические распределения характеризуются форму­лами, приведенными в математических справочниках. Например, плотно­сти нормального и логарифмически нормального законов распределения имеют соответственно запись:

(3.59)

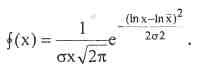(3.60)

Законы распределения имеют также аналитические выражения:

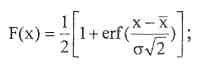(3.61)

(3.62)

3.63)

erf(х)–интеграл вероятности, значения которого табулированы в ма­тематических справочниках.

В практике отображения неоднородностей пород помимо вероятно­стно-статистических методов используют детерминированные методы на базе корреляции разрезов, когда применяют коэффициенты песчанистости, расчлененности, слияния и пр.

51