
- •Мухаметьянов Ильдар Талгатович методические материалы к изучению линейной алгебры
- •Часть 1. Матрицы и определители
- •Содержание
- •Предисловие
- •Доцент Мухаметьянов Ильдар Талгатович
- •Глава I. Матрицы
- •§1. Основные понятия
- •§2. Действия с матрицами
- •2.1. Сложение матриц и его свойства
- •2.2. Умножение матрицы на число и его свойства.
- •2.3. Произведение матриц и его свойства.
- •2.4. Упражнения.
- •2.5. Элементарные преобразования матриц.
- •Глава II. Определители
- •§1. Понятие определителя
- •1.1. Определители 2-го и 3-го порядков
- •1.3. Общее понятие определителя
- •§2. Свойства определителей и их вычисление
- •2.1. Свойства определителей
- •2.3. Упражнения.
- •§3. Некоторые применения определителей
- •3.1. Ранг матрицы и методы его нахождения.
- •3.2. Обратная матрица и её нахождение.
- •3.3. Упражнения.
- •Литература
2.4. Упражнения.
2.4.1. Выполнить действия:
а) 4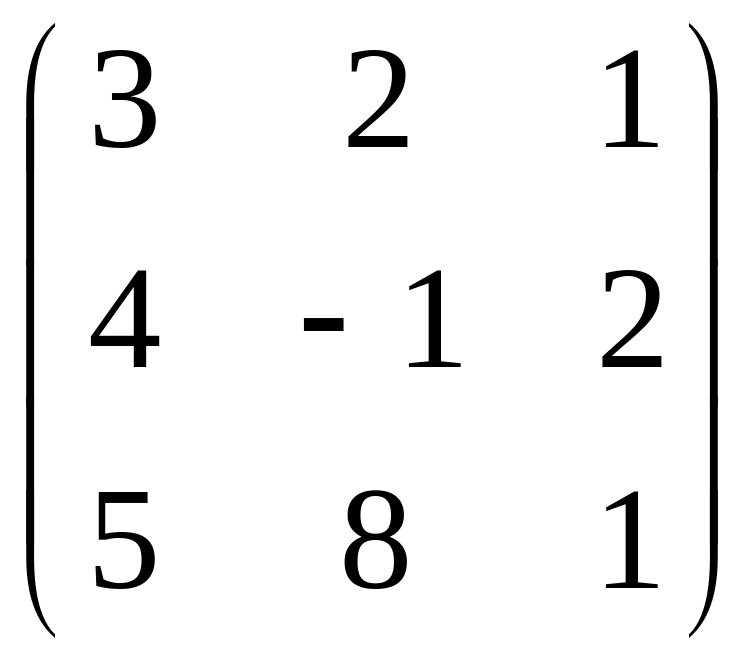 2
2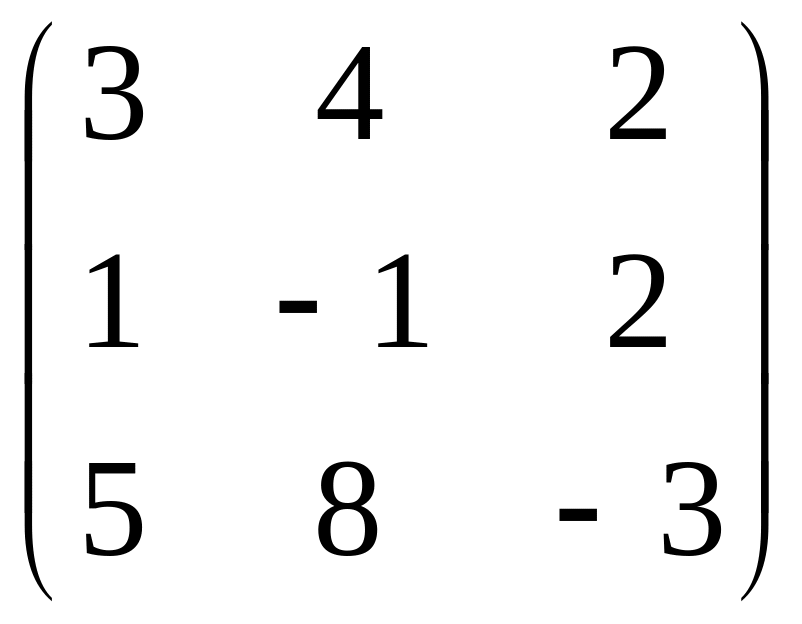 ;
б) 3
+4
;
;
б) 3
+4
;
в) 2
3
+4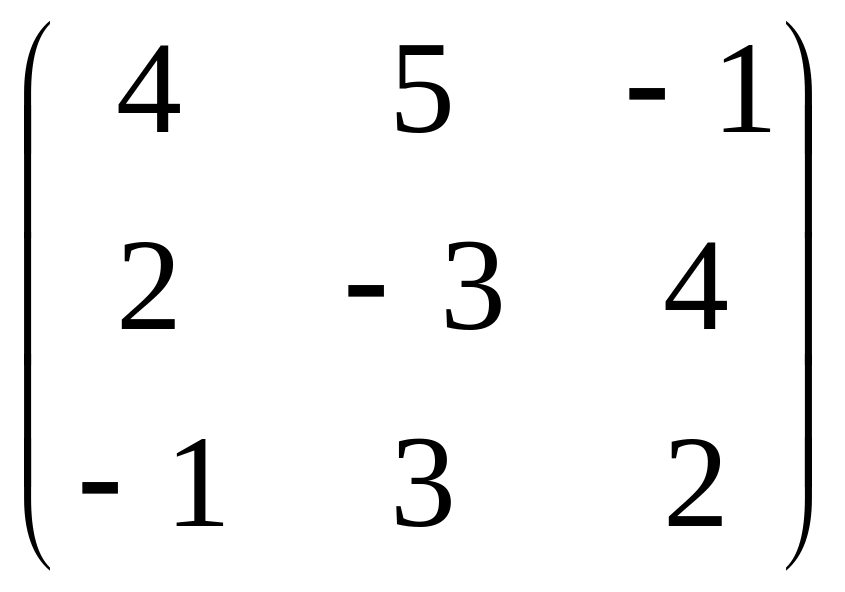 .
.
2.4.2. Найти произведения AB, BA, ATBT, BTAT, если:
а)
A=(2,
3, 4), B=(2,
1, 3)T;
б)
A=(2,
3, 4), B= ;
;
в)
A=![]() ,
B=
,
B=![]() ;
г)
A=
,
B=
;
;
г)
A=
,
B=
;
д) A= , B= , е) A= , B= .
Решение. в) AB не определено, так как число 3 столбцов A не совпадает с числом 2 строк B.
BA=
=![]() =
=![]() .
.
Так как ATBT=(BA)T,
то ATBT=![]() =
=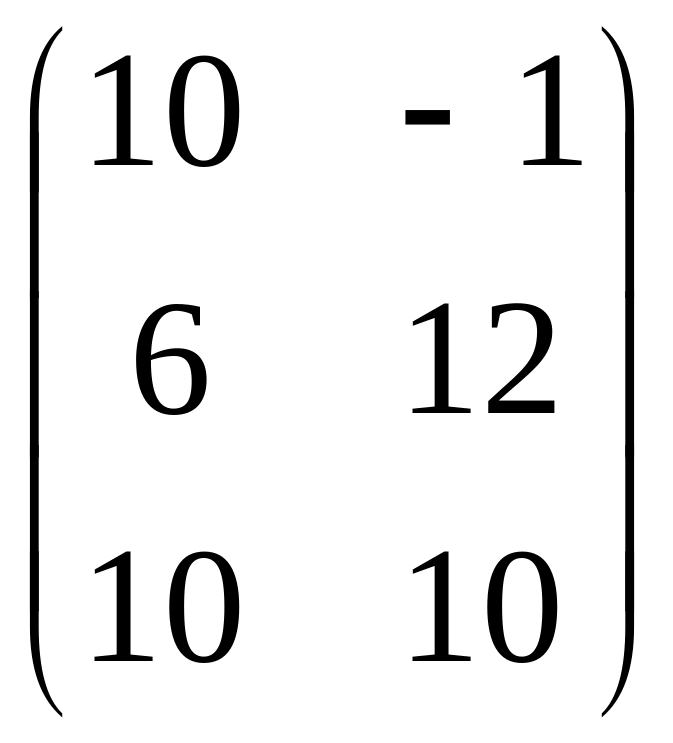 .
Так как AB
не определено, то не определено и
BTAT=(AB)T.
.
Так как AB
не определено, то не определено и
BTAT=(AB)T.
Ответ: в) AB и BTAT не определены, BA= , ATBT= .
2.4.3. Вычислить:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
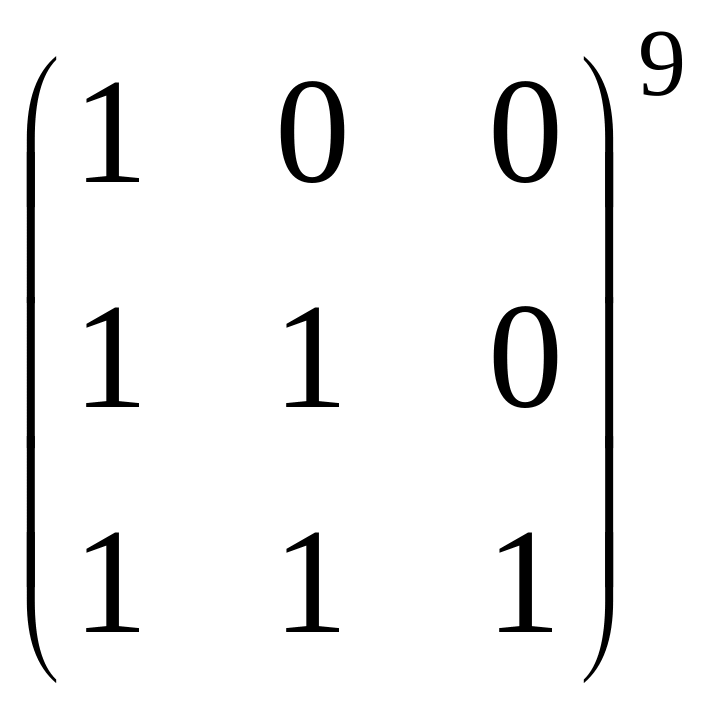 .
.
Решение.
б)
![]() =
=![]() =
=![]() ,
,
=
=
=![]() .
.
Замечаем, что
![]() =
=![]() .
Поэтому
=
.
Поэтому
=![]() .
.
Ответ: б) .
2.4.4. Вычислить:
а)
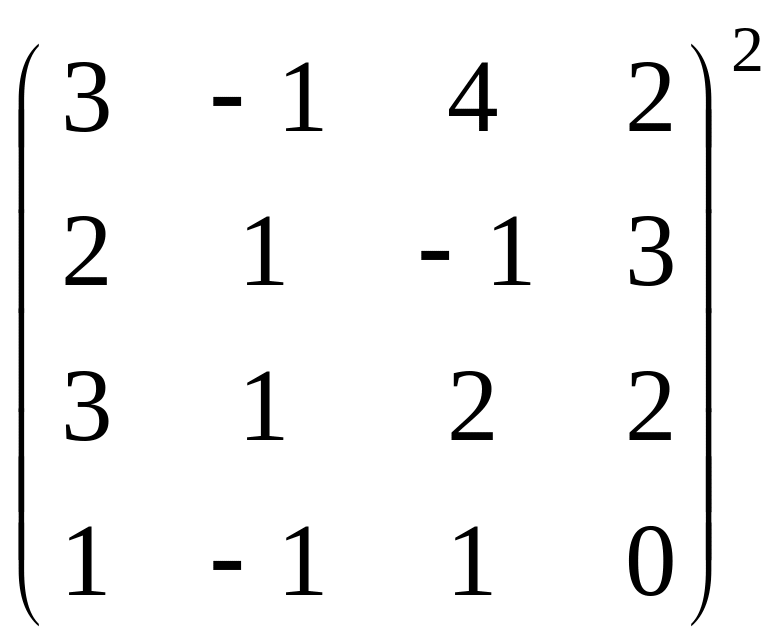 +6
+6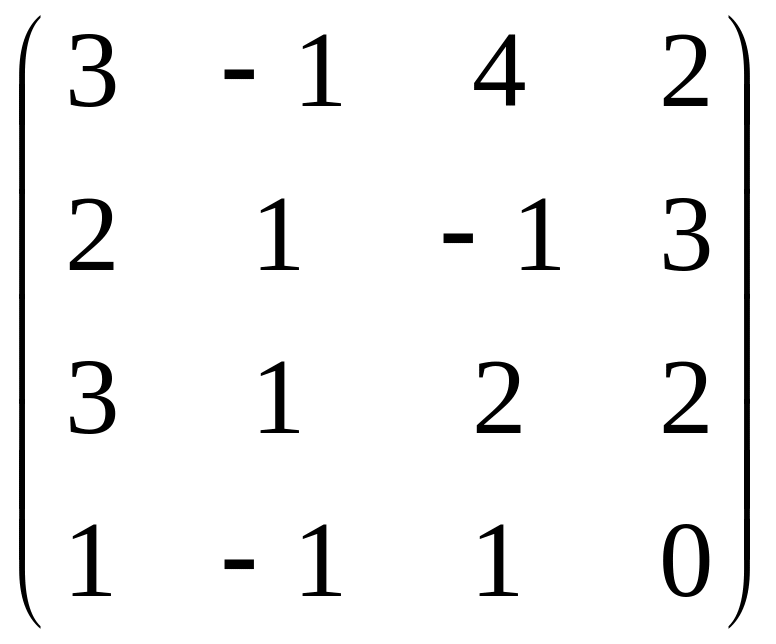
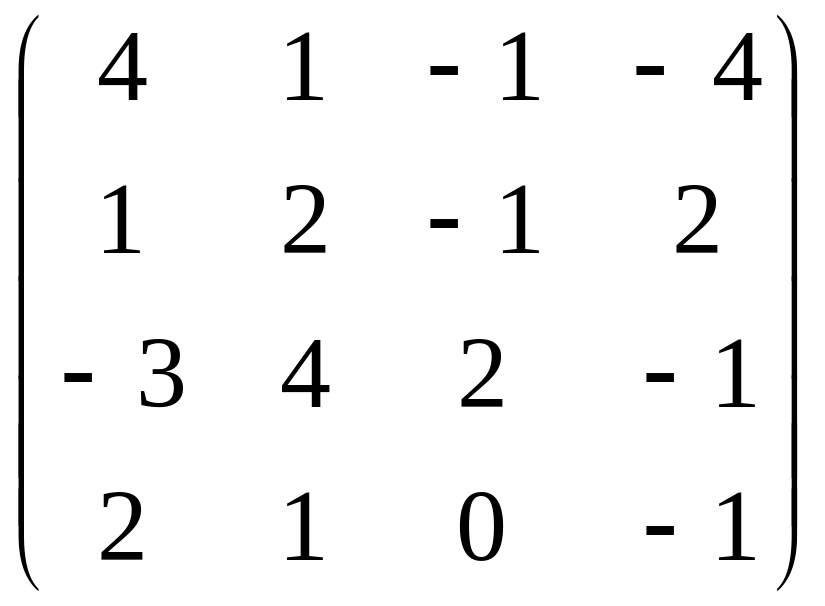
2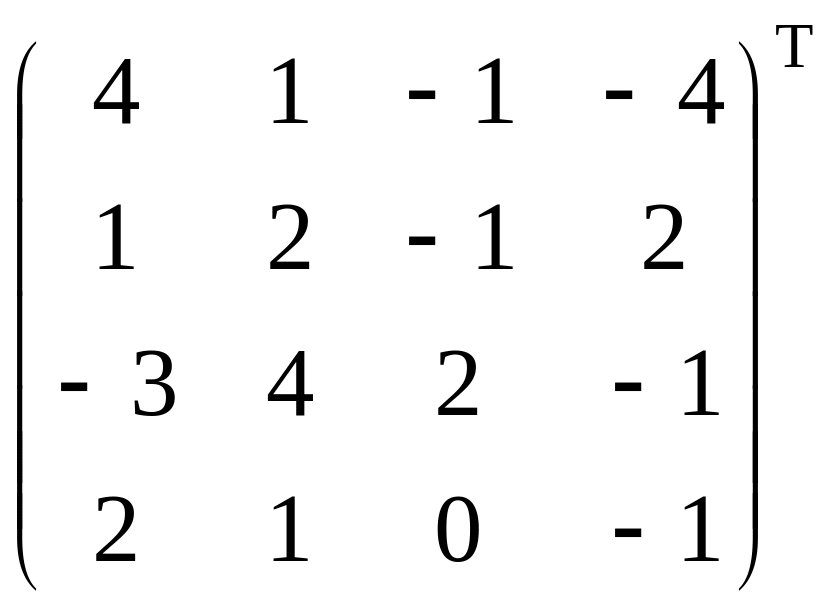
 ;
;
б)
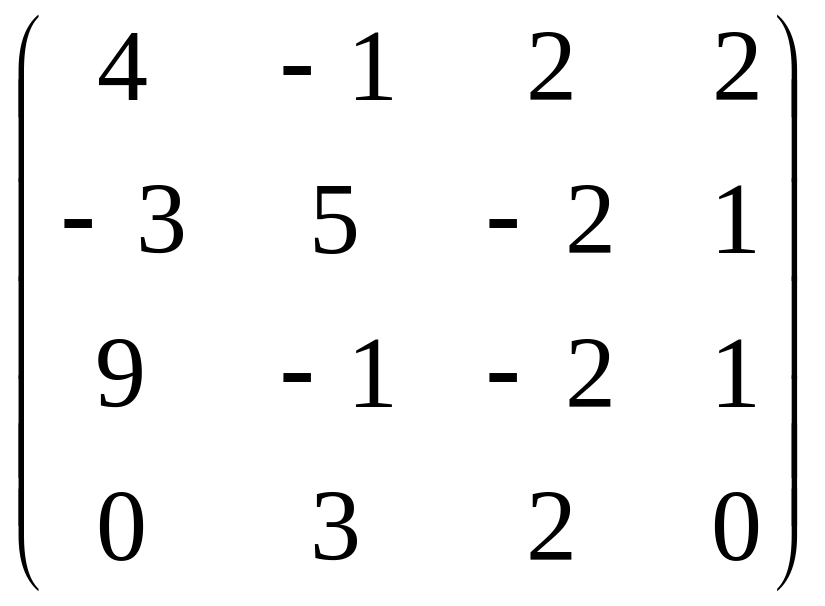 +
+
+3
 ;
;
Решение. а) Выполним вычисления по действиям:
1) = =
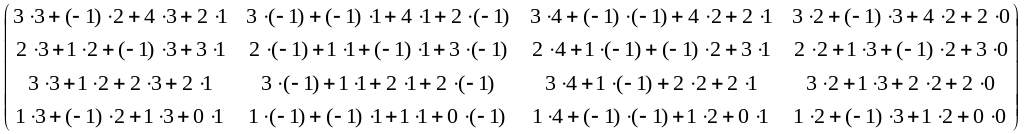 =
=
=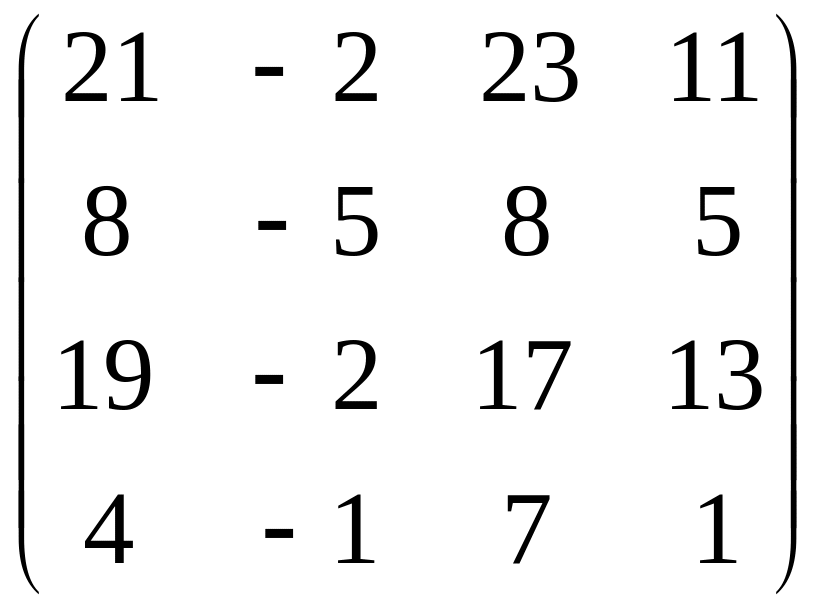
2) =
 =
=
=
3) 6 =6 =
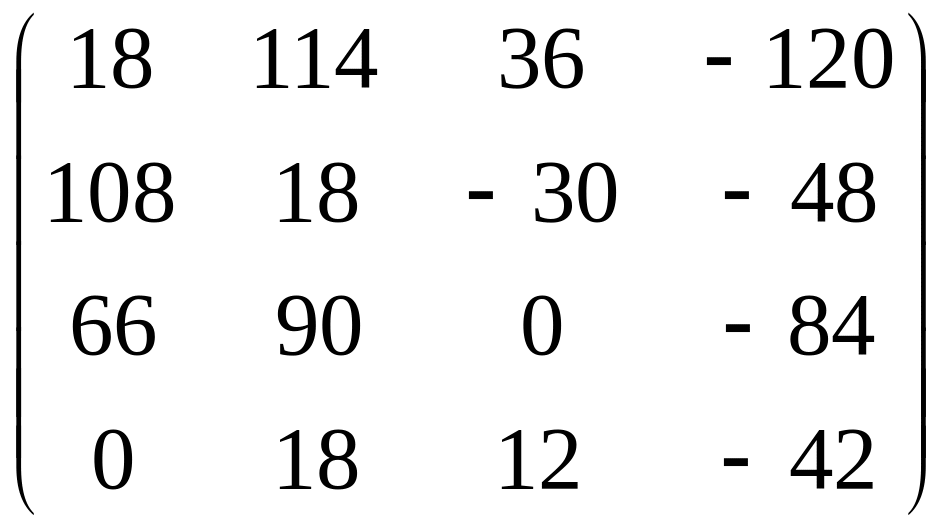
4) Так как BTAT=(AB)Т, то
=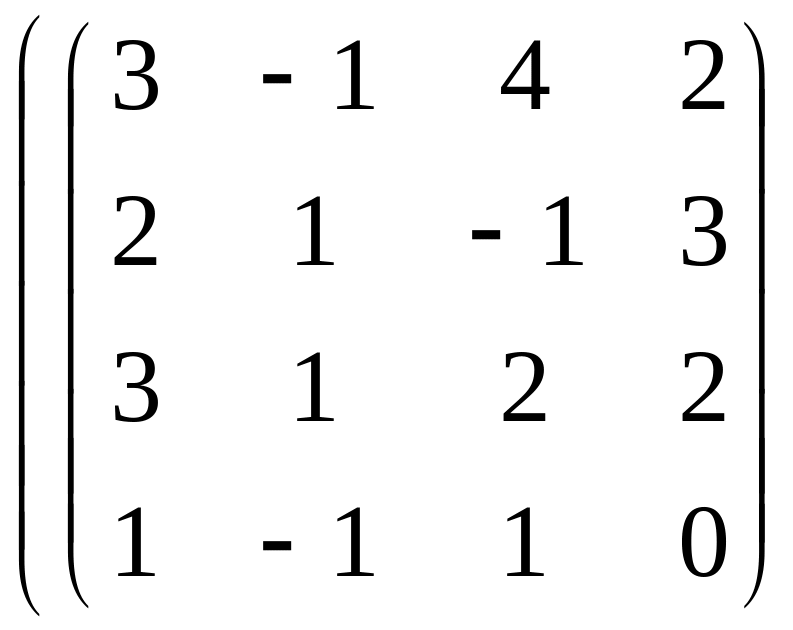
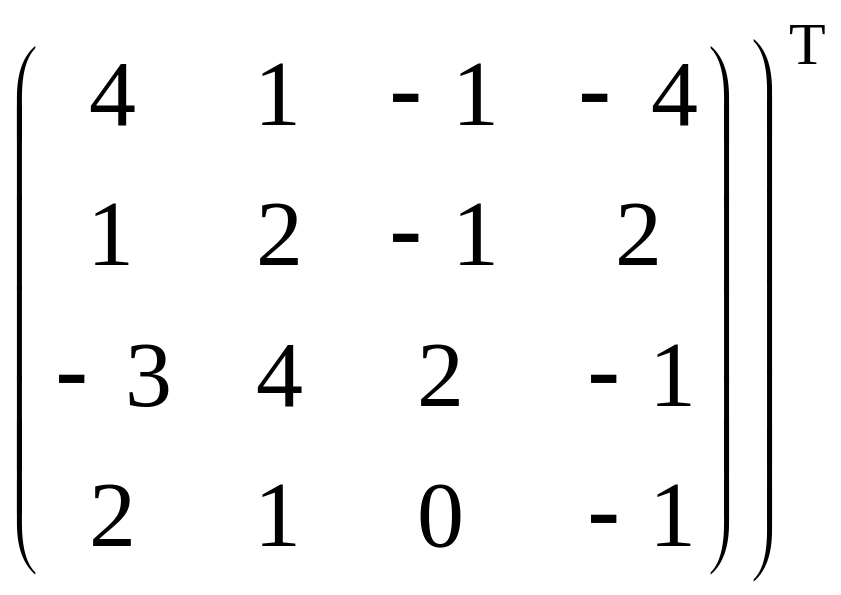 =
=
=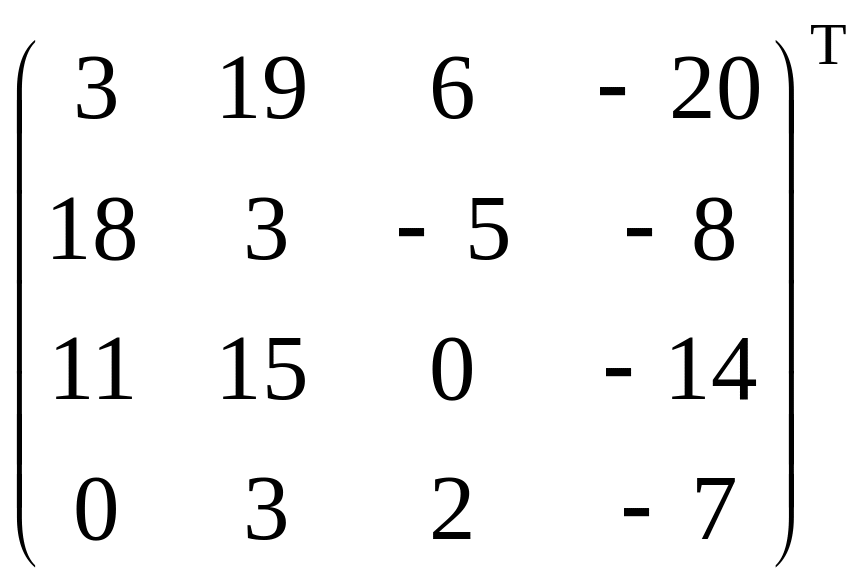 =
=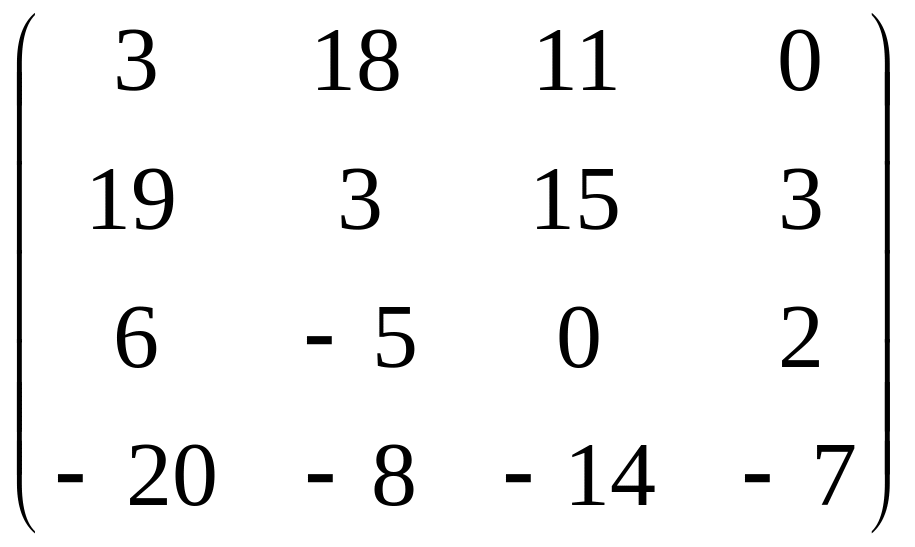
5) 2 =2 =
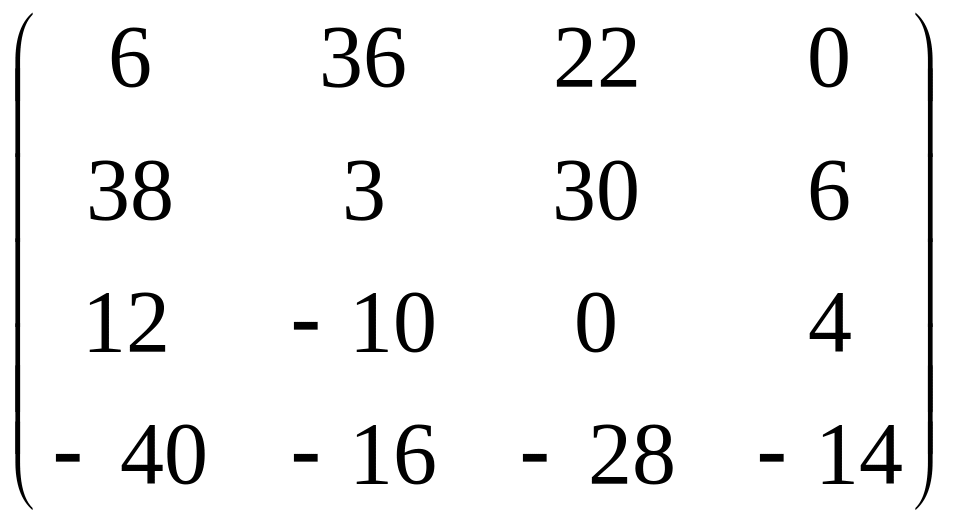
6) +6
2 =
= + =
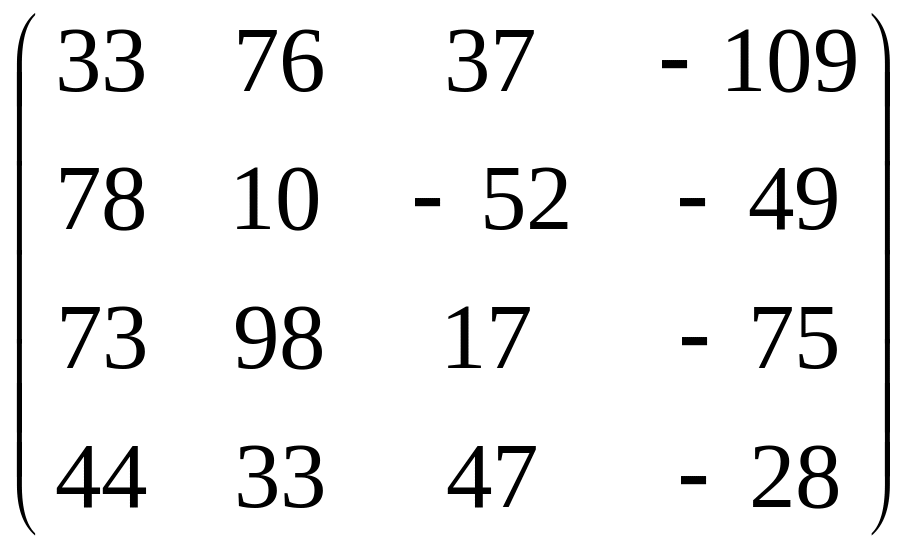
Ответ: а)
2.5. Элементарные преобразования матриц.
2.5.1. Определение. Элементарными преобразованиями строк матрицы называется преобразования следующих типов:
1) Умножение каждого элемента некоторой строки на одно и то же ненулевое число. Остальные строки остаются без изменения (кратко: умножение строки на число).
2) Прибавление к каждому элементу некоторой строки соответствующих элементов другой строки, умноженные на одно и то же число. Остальные строки (в том числе и прибавляемое) остаются без изменения (кратко: прибавление к строке другой, умноженной на число).
3) Перемена местами некоторых двух строк матрицы. Остальные строки остаются без изменения.
Эти преобразования называются соответственно преобразованиями первого, второго и третьего типа (рода). Последовательно применяя их, мы получаем более сложные преобразования.
Аналогично определяются элементарные преобразования столбцов матрицы.
2.5.2. Теорема. Преобразование третьего типа является некоторой комбинацией преобразований первого и второго типов.
Таким образом, преобразованием третьего типа можно отнести к более сложным, чем элементарные. Но его принято всё-же считать элементарным ради удобства.
2.5.3. Теорема. Любую матрицу элементарными преобразованиями строк можно привести к ступенчатой. Если к матрице применить элементарные преобразования строк и столбцов, то её можно привести к трапециедальному виду.
Например,

![]() 1
1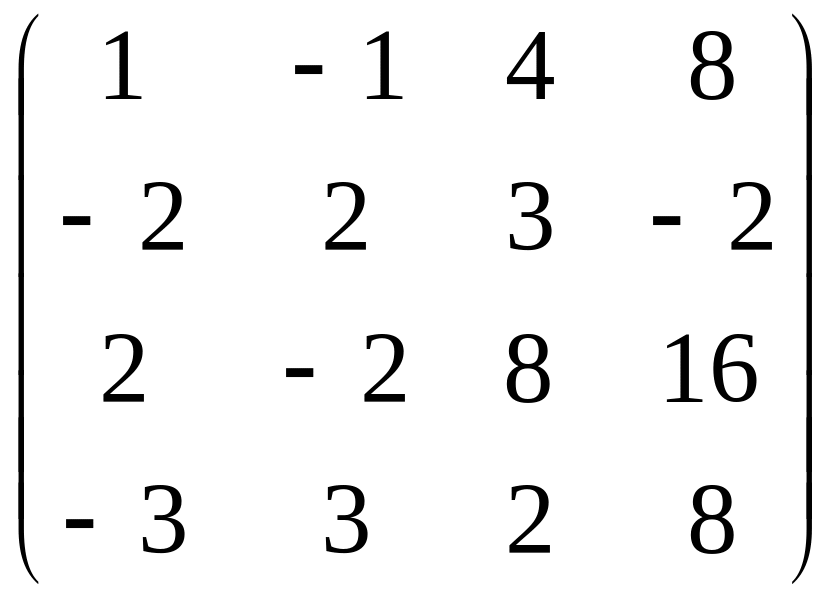
![]()

![]()

![]()
(1) Поменяли местами первую и вторую строки (преобразование третьего типа).
(2) Первую строку, умноженную на 2, прибавили ко второй и вычли из третьей, умноженную на 3, прибавили к четвёртой (преобразования второго типа).
(3) Вторую строку вычли из третьей и вторую строку, умноженную на 14/11 вычли из четвёртой.
(4) Поменяли местами третью и четвёртую строки.
Таким образом, преобразовали исходную матрицу
в ступенчатую
.
Теперь, поменяв местами второй и третий столбец, а затем поменяв его же с четвёртым столбцом, перемещаем второй столбец на место четвёртого, третий и четвёртый столбцы окажутся соответственно на месте второго и третьего столбцов:
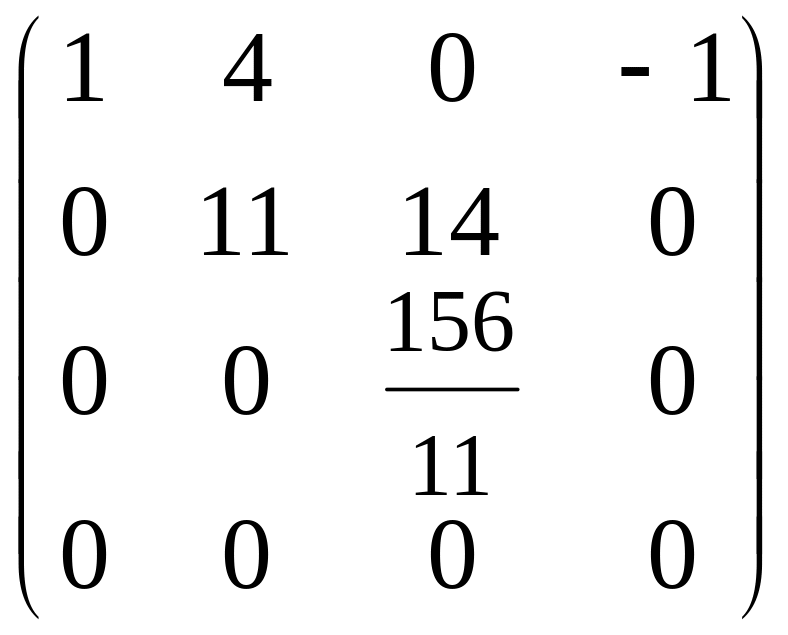 ,
,
тем самым преобразовали исходную матрицу в трапециедальную.
2.5.4. Упражнения. Привести матрицу к ступенчатому и трапециедальному видам:
а)
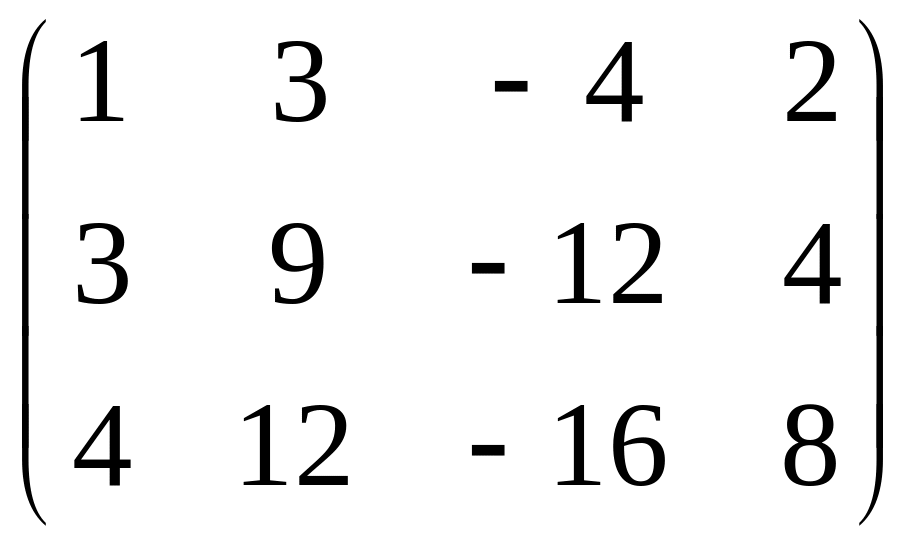 ;
б)
;
б)
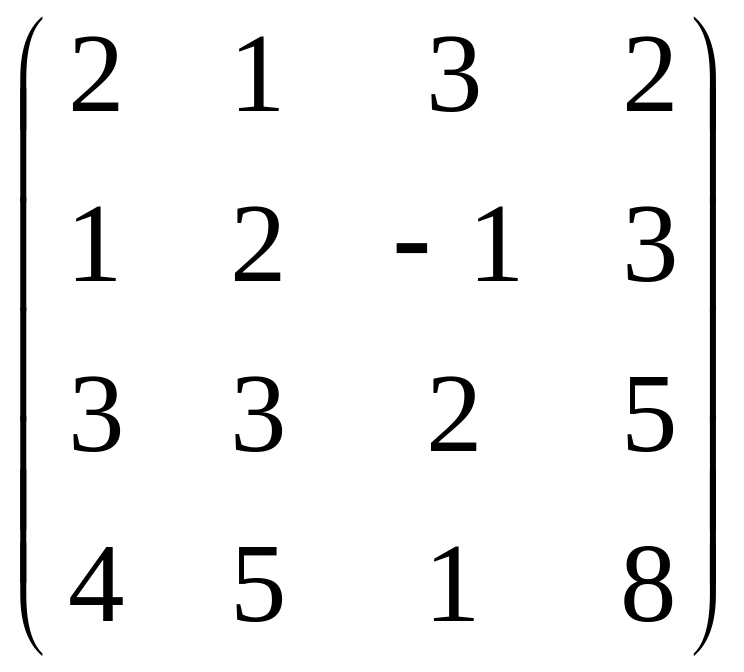 ;
;
в)
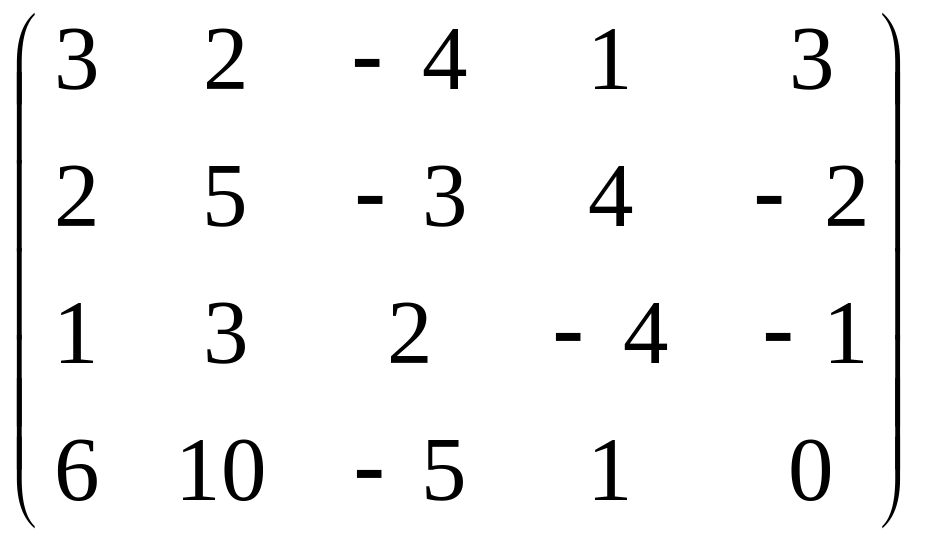 ; г)
.
; г)
.
