Вопрос 39

Определение дифференциальных уравнений

Дифференциальные уравнения – это соотношение вида F(x₁,x₂,x₃,..,y,y′,y′′,...y⁽ⁿ⁾) = 0, связывающее независимые переменные x₁,x₂,x₃,... функцию y этих независимых переменных и ее производные до n-го порядка. При этом функция F определена и достаточное число раз дифференцируема в некоторой области изменения своих аргументов.

Обыкновенные дифференциальные уравнения – это дифференциальные уравнения, в которых содержится только одна независимая переменная.

Дифференциальные уравнения в частных производных – это дифференциальные уравнения, в которых содержится две и более независимых переменных.

Если ясно, какое уравнение рассматривается, то слова “обыкновенные“ или "в частных производных" могут опускаться. В дальнейшем рассматриваются обыкновенные дифференциальные уравнения.

Классификация дифференциальных уравнений

Порядок дифференциального уравнения – это порядок старшей входящей в него производной.

Степень дифференциального уравнения – это показатель степени, в которую возведена производная наивысшего порядка.

Вот пример уравнения первого порядка второй степени:    Вот пример уравнения четвертого порядка первой степени: 

Иногда дифференциальные уравнения записывают в виде, в котором входят дифференциалы:  (x² - 3xy²)dx + (xy² - 3x²y)dy = 0  В этом случае переменные x и y следует полагать равноправными. Если необходимо, такое уравнение можно привести к виду, в котором явно содержится производная y'.  Разделим на dx: 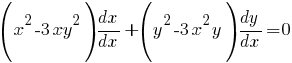   поскольку   и  , то уравнение принимает вид, содержащим производную первого порядка: 

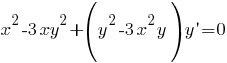
Решение дифференциальных уравнений

Если производные от элементарных функций выражаются через элементарные функции, то выразить интеграл через элементарные функции удается не всегда. С дифференциальными уравнениями дело обстоит еще хуже. В результате решения можно получить:

• явную зависимость функции от переменной.

Решение дифференциального уравнения – это функция y(x), определенная и достаточное число раз дифференцируемая в некоторой области, при подстановке которой в исходное уравнение получается тождество.

• неявную зависимость в виде уравнения типа Ф(y,x)=0 или системы уравнений;

Интеграл дифференциального уравнения – это решение дифференциального уравнения, которое имеет неявный вид.

• зависимость, выраженную через элементарные функции и интегралы от них;

Решение дифференциального уравнения в квадратурах – это нахождение решения в виде комбинации элементарных функций и интегралов от них.

• решение может не выражается через элементарные функции;

Поскольку решение дифференциальных уравнений сводится к вычислению интегралов, то в состав решения входит набор постоянных C₁,C_2,C₃,...C_n. Количество постоянных равно порядку уравнения.

Общее решение дифференциального уравнения – это соотношение видаy = y(x,C₁,C_2,C₃,...C_n), зависящее от n произвольных постоянных.

Общий интеграл дифференциального уравнения – это общее решение, которое имеет неявный вид Ф(x,y,C₁,C_2,C₃,...C_n) = 0.

Частное решение дифференциального уравнения – это общее решение при заданных значениях постоянных C₁,C_2,C₃,...C_n.

Частный интеграл дифференциального уравнения – это общий интеграл при заданных значениях постоянных C₁,C_2,C₃,...C_n.