§4. Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра

Чтобы получить теоретическую изотерму адсорбции, описывающую широкую область концентраций, необходимо использование представлений о механизме адсорбции и конкретных моделей.

Адсорбция рассматривается как квазихимическая реакция между адсорбатом и адсорбционными центрами поверхности адсорбента. В этом заключается основная идея адсорбционной теории Ленгмюра, которая явилась фундаментальным вкладом в учение об адсорбции. Ограниченность поверхности адсорбента приводит к ее адсорбционному насыщению по мере увеличения концентрации распределяемого вещества. Это положение теории Ленгмюра уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; в результате образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны - поверхность адсорбента эквипотенциальна; 3) адсорбированные молекулы не взаимодействуют друг с другом. 4) адсорбция обратима.

Для получения уравнения изотермы обратимся к основному положению теории Ленгмюра. Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:

↔

где - адсорбционные центры поверхности; В - распределяемое вещество; - комплекс, образующийся на поверхности.

По мере увеличения концентрации (давления) вещества В реакция сдвигается в сторону образования комплекса и свободных адсорбционных центров становится меньше. Константа адсорбционного равновесия равна

(IX.6)

В этом соотношении

(IX.7)

где А - величина адсорбции вещества В; A_ - емкость адсорбционного монослоя, или число адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента); А₀ - число оставшихся свободными адсорбционных центров, приходящихся на единицу площади поверхности (или на единицу массы адсорбента).

Подставляя уравнения (IX.7) в уравнение (IX.6), получим:

Опуская индекс при обозначении концентрации адсорбата С_В , после простых преобразований окончательно имеем:

(IX.8)

Выражение (IX.8) называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Так как концентрации газов и паров практически пропорциональны парциальным давлениям, то для них изотерма адсорбции Ленгмюра принимает вид:

(IX.9)

Необходимо отметить, что константа адсорбционного равновесия в уравнении Ленгмюра характеризует энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше константа адсорбционного равновесия.

Адсорбционное уравнение Ленгмюра часто представляют относительно степени заполнения поверхности - отношения величины адсорбции А к емкости монослоя А_

(IX.10)

Типичная изотерма адсорбции Ленгмюра показана на рис.20.

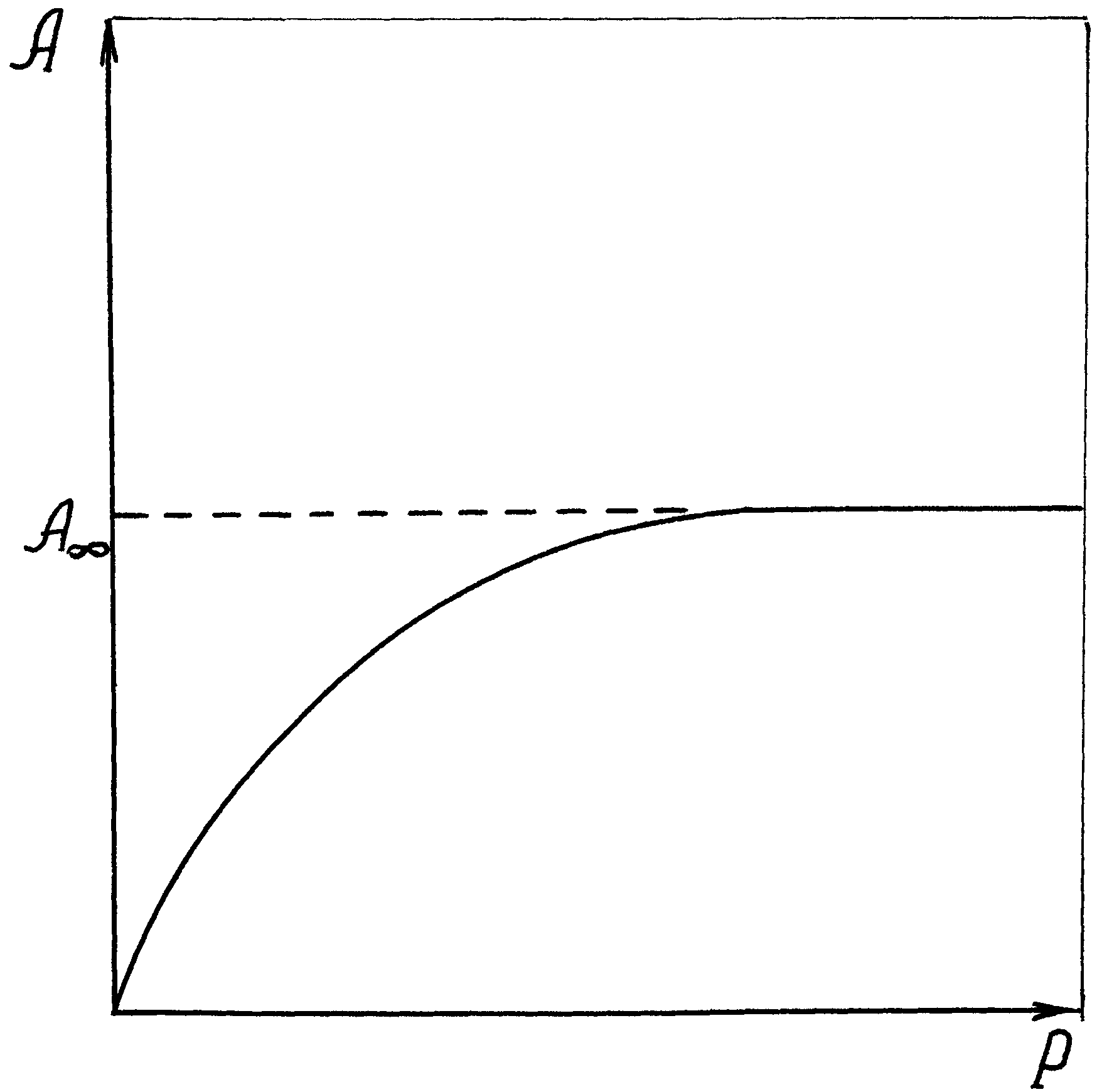
Рис.20. Изотерма адсорбции Ленгмюра

Важны экстраполяционные следствия из соотношений (IX.8) - (IX.9). При малых концентрациях или давлениях, когда с  0, получаем:

и (IX.11)

Выражения (IX.11) соответствуют закону Генри: величина адсорбции линейно растет с увеличением концентрации.

При больших концентрациях и давлениях, когда КC >> 1 и KP>> 1, уравнения (IX.8) — (IX.9) переходят в соотношения:

и (IX.12)

Соотношения (IX.12) отвечают состоянию насыщения, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. Экспериментальное определение А_ позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента):

(IX.12a)

где А_ -предельная адсорбция, выражаемая числом молей адсорбата на единицу массы адсорбента; N_A - число Авогадро; - площадь, занимаемая одной молекулой адсорбата.

Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме (числитель (IX.8) переносят в знаменатель, а знаменатель - в числитель):

(IX.13)

Если обе части уравнения (IX.13) умножить на С, то получим еще одну форму записи указанного уравнения, дающего линейную зависимость в координатах и С:

(IX.13а)

Такая линейная зависимость позволяет графически определить оба постоянных параметра (А_ и К) адсорбционной изотермы. На рис.21 представлена типичная изотерма адсорбции в координатах уравнения (IХ.13а). Экстраполяция зависимости до оси ординат дает отрезок, равный 1/(А_K), а тангенс угла наклона прямой к оси абсцисс равен 1/ А_,

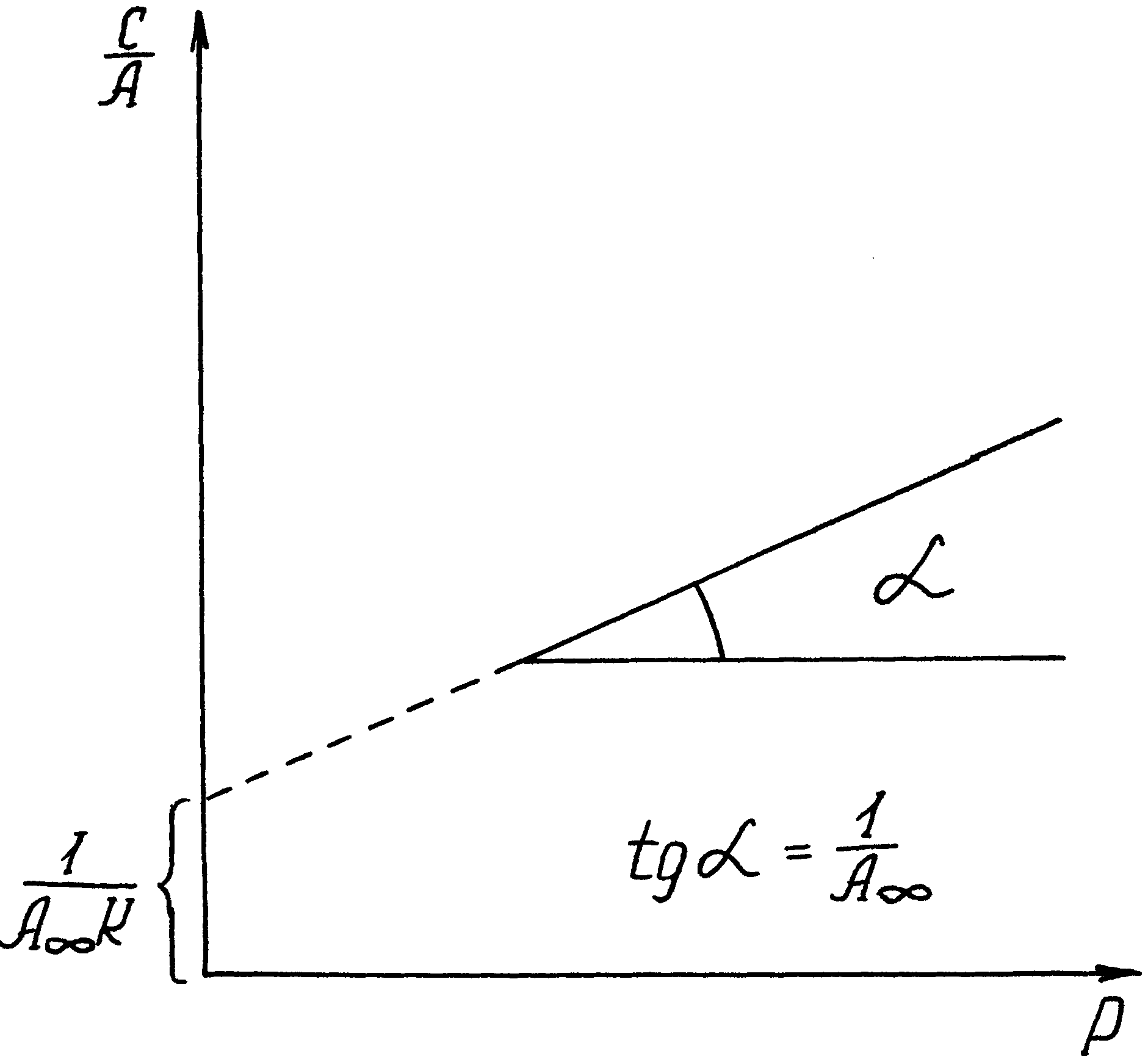
Рис.21. Изотерма адсорбции в координатах линейной формы уравнения Ленгмюра (IX.13а)

При адсорбции газов из их смесей в соответствии с уравнением изотермы Ленгмюра величины адсорбции суммируются, а концентрация свободных центров A₀ является общей для равновесной многокомпонентной системы.

Степень заполнения для i-oго компонента составит:

(IX.14),

где P_i - парциальное давление i-oго компонента, а K_i - его адсорбционная константа равновесия.

Из уравнения (IX.14) следует, что увеличение парциального давления одного компонента подавляет адсорбцию других, и тем сильнее, чем больше его адсорбционная константа равновесия.

Все рассмотренные до сих пор уравнения справедливы для мономолекулярной адсорбции, протекающей на адсорбенте с энергетически эквивалентными адсорбционными центрами. Однако реальные поверхности твердых тел, как правило, не обладают такими свойствами. Для приближения к реальным условиям целесообразно рассмотрение возможных распределений адсорбционных центров поверхности адсорбента по энергиям. Приняв экспоненциальное распределение адсорбционных центров по энергиям, в области средних заполнений получается найденное эмпирически уравнение Фрейндлиха:

(IX.15)

где К и п — постоянные.

Уравнение Фрейндлиха широко используется при обработке экспериментальных адсорбционных данных, в том числе в инженерных расчетах. Чаще всего оно применяется в логарифмической форме

позволяющей построить линейную зависимость lnA - ln P и графически определить оба постоянных параметра K и п.