§ 2. Закон Рауля. Идеальные растворы. Предельно разбавленные растворы

В простейшем случае зависимость парциального давления пара растворителя от состава бинарного раствора имеет следующий вид:

(V, 1)

Парциальное давление растворителя в паровой фазе пропорционально его мольной доле в растворе.

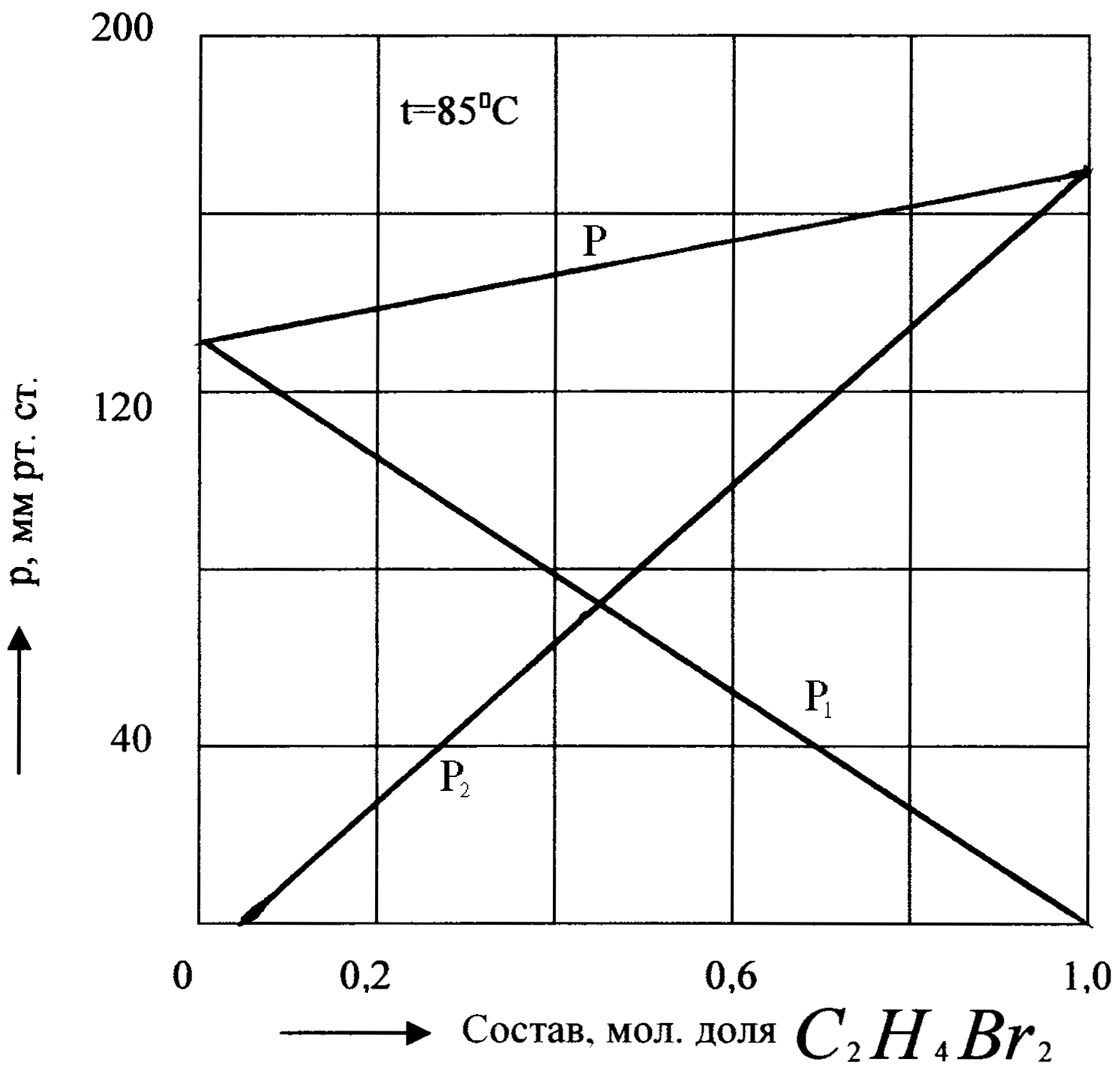
Рис.5. Общее и парциальные давления пара бинарного раствора: дибромпропан - дибромэтан. Парциальные давления на диаграмме P – x изображаются прямыми линиями.

Уравнению (V, 1) можно придать иной вид:

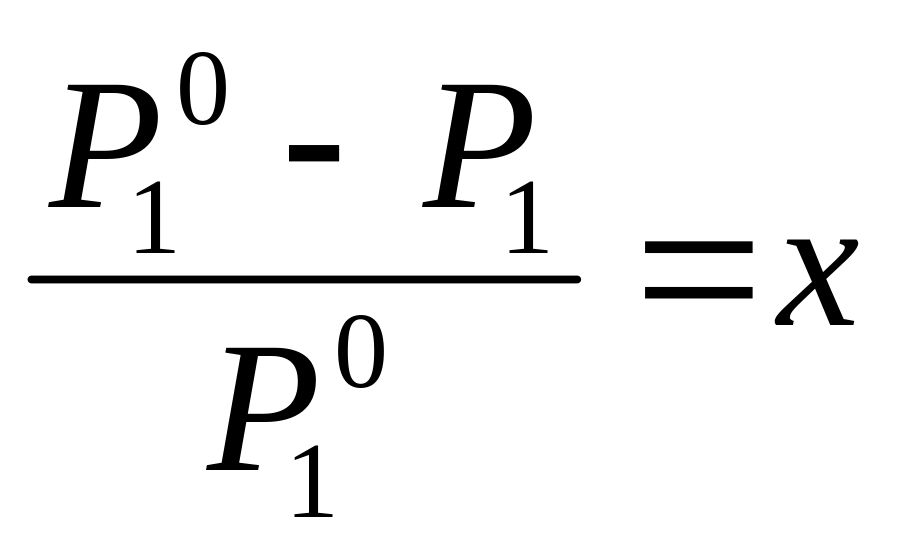(V, 2)

Относительное понижение парциального давления растворителя в паровой фазе равно мольной доле растворенного вещества (второго компонента). Уравнения (V, 1) и (V, 2) являются выражениями закона Рауля (1886). Закон Рауля, выраженный в форме уравнения (V, 1), применим к таким растворам, насыщенный пар которых ведет себя как идеальный газ, причем лишь немногие растворы подчиняются с достаточной точностью этому закону, при любых концентрациях (т. е. при значениях x, изменяющихся в интервале от 0 до 1).

Обычно при повышении температуры (пока давление насыщенного пара относительно невелико) отклонения от закона Рауля в форме (V, 1) уменьшаются. Но при достаточно высоких температурах, когда давление насыщенного пара раствора очень велико, уравнение (V, 1) становится неточным, так как возрастают отклонения пара от закона идеальных газов.

Растворы, следующие закону Рауля в форме уравнения (V, 1) при всех концентрациях и всех температурах, называются идеальными (совершенными) растворами, они являются предельным, простейшим типом жидких растворов.

Легко показать, что если для пара растворителя соблюдается уравнение (V, 1), то должно соблюдаться аналогичное уравнение для пара второго, растворенного компонента

(V, 3)

Уравнения (V, 1) и (V, 3) отражают свойства парциальных давлений идеальных растворов при малых давлениях. Совокупность этих уравнений носит название объединенного закона Рауля - Генри. В общем виде для многокомпонентного идеального раствора при невысоких давлениях получим:

(V, 4)

Уравнения (V, 1), (V, 3) и (V, 4) будут в дальнейшем изложении служить исходными для изучения термодинамических свойств идеальных растворов при небольших давлениях.

Полное давление пара идеального бинарного раствора, равное

(V, 5)

является также линейной функцией мольной доли.

Примерами идеальных растворов могут служить смеси (см. рис.5), бензол -толуол, бензол - дихлорэтан, гексан - октан и другие.

Составы идеального раствора и его насыщенного пара различны, т. е. х. В данном случае легко найти связь между и х. В самом деле, концентрация второго компонента в паре . Подставив в это выражение значение P₂ из закона Рауля (уравнение (V, 3)) и значение P из уравнения (V, 5), получим:

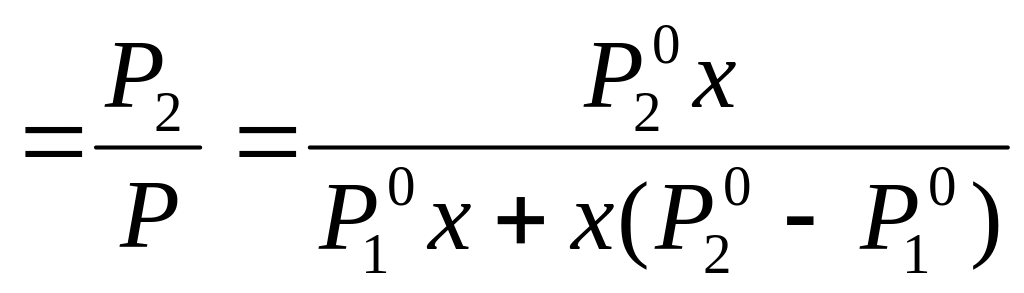(V, 6)

Отсюда видно, что = х только при равенстве давлений насыщенного пара обоих чистых компонентов, т.е. при .

§ 3. Реальные растворы. Положительные и отрицательные отклонения от закона Рауля

Закон Рауля не выполняется для реальных растворов. Парциальные давления этих растворов больше или меньше давлений паров идеальных растворов. Отклонения от закона Рауля в первом случае называются положительными (общее давление пара больше аддитивной величины), а во втором случае - отрицательными (общее давление пара меньше аддитивной величины).

Примерами растворов с положительными отклонениями от законов Рауля могут служить растворы:

Ацетон - этиловый спирт

Бензол - ацетон

Вода - метиловый спирт

На рис.6 изображена диаграмма P - х для одного из этих растворов (бензол - ацетон).

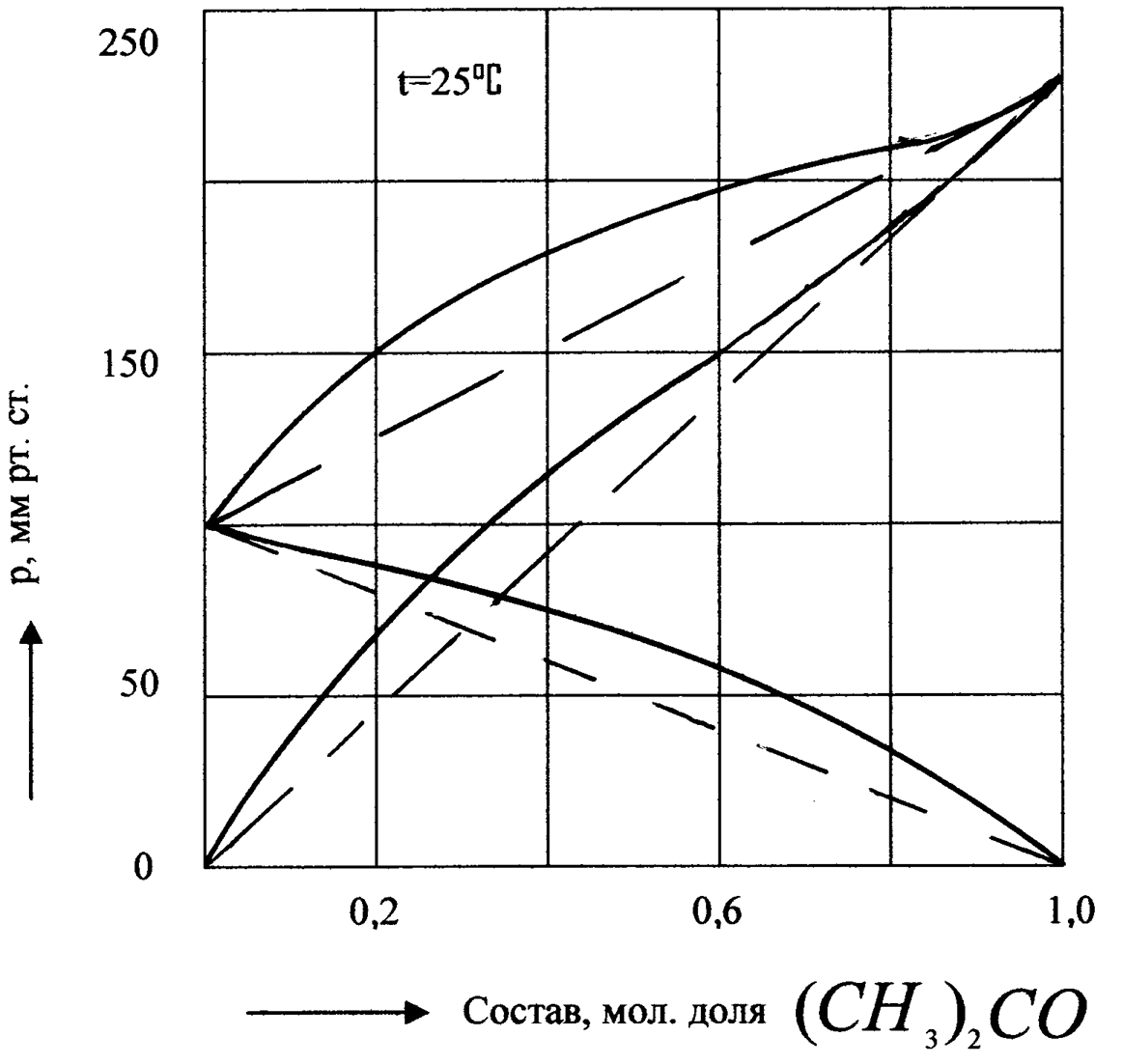
Рис.6. Диаграмма давления пара над раствором С₆Н₆ - (СН₃)₂СО.

К растворам с отрицательными отклонениями от законов Рауля относятся, например, растворы:

Хлороформ - бензол

Хлороформ - этиловый эфир

Диаграмма давления пара над раствором хлороформ - диэтиловый эфир показана на рис.7.

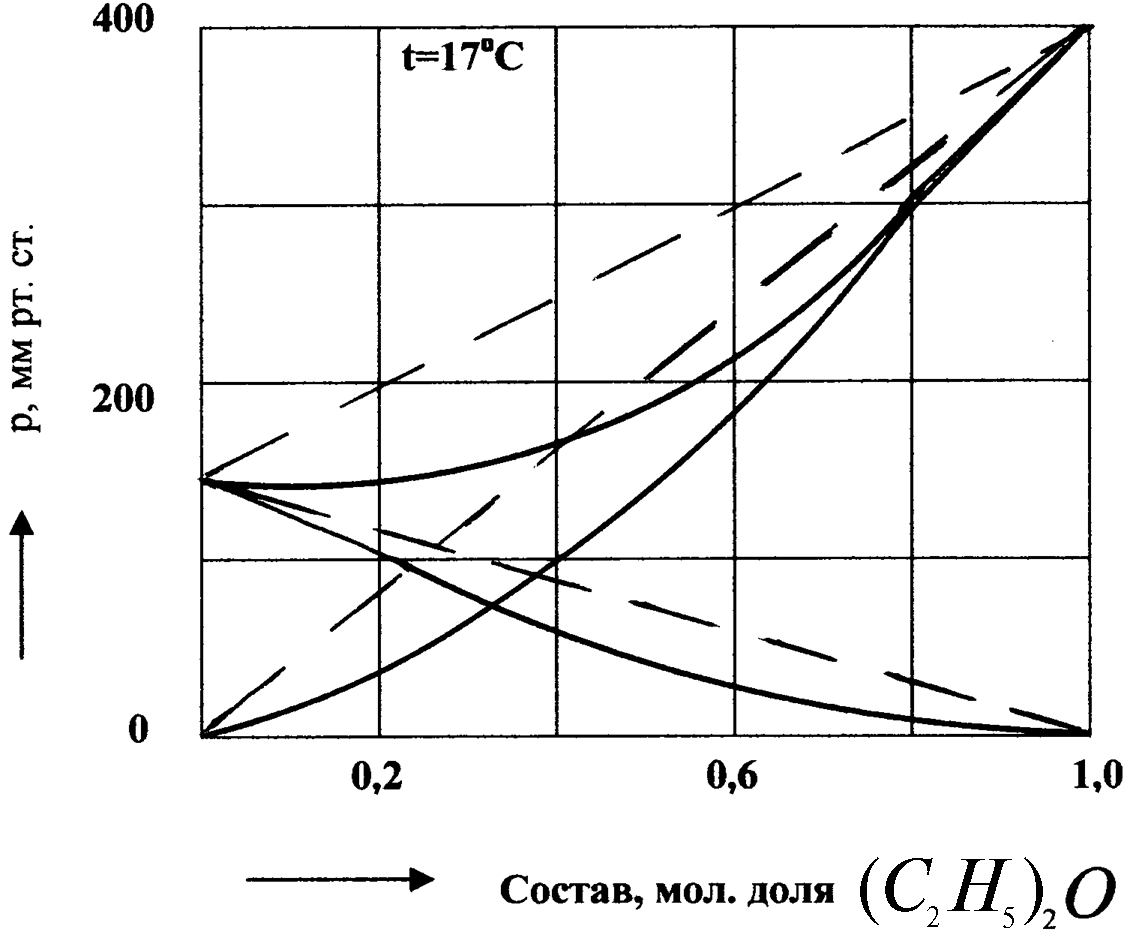
Рис.7. Диаграмма давления пара над раствором (С₂Н₅)₂О - СНСl₃.

Величины общего давления P в этих системах изменяются монотонно с изменением величины х. Если отклонения от закона идеальных растворов велики, то кривая общего давления пара проходит через максимум или минимум.

Положительные и отрицательные отклонения реальных растворов от закона Рауля обусловлены разными факторами. Если разнородные молекулы в растворе взаимно притягиваются с меньшей силой, чем однородные, то это облегчит переход молекул из жидкой фазы в газовую фазу (по сравнению с чистыми жидкостями) и будут наблюдаться положительные отклонения от закона Рауля. Усиление взаимного притяжения разнородных молекул в растворе (сольватация, образование водородной связи, образование химического соединения) затрудняет переход молекул в газовую фазу, поэтому будут наблюдаться отрицательные отклонения от закона Рауля.

Следует иметь в виду, что факторы, вызывающие положительные и отрицательные отклонения, могут действовать в растворе одновременно, поэтому наблюдаемые отклонения часто являются результатом наложения противоположных по знаку отклонений. Одновременное действие противоположных факторов особенно наглядно проявляется в растворах, в которых знак отклонений от закона Рауля - Генри изменяется с изменением концентрации.