§ 3. Методы расчета энтропии

Уравнения (II, 1) и (II, 1а), определяющие энтропию, являются единственными исходными уравнениями для термодинамического расчета изменения энтропии системы. Заменяя элементарную теплоту в уравнении (II, 1а) ее выражениями через калорические коэффициенты (см. уравнения (I, 10) и (I, 10а)), получаем для равновесных процессов:

dS = = + (II, 3)

dS = + (II, 3а)

Уравнения (II, 3) и (II, 3а) являются полными дифференциалами энтропии как функции переменных V, Т или P, Т. Коэффициенты этих уравнений - частные производные энтропии по соответствующим переменным.

Подставив в уравнение (II, 3) значения калорических коэффициентов для одного моля идеального газа: l = P = RT/V [уравнение (I, 24)] и h = –V = –RT/P [уравнение

(I, 25) и полагая С_V и С_P независимыми от температуры (что допустимо лишь в небольших температурных интервалах), получим после интегрирования в известных пределах:

S = 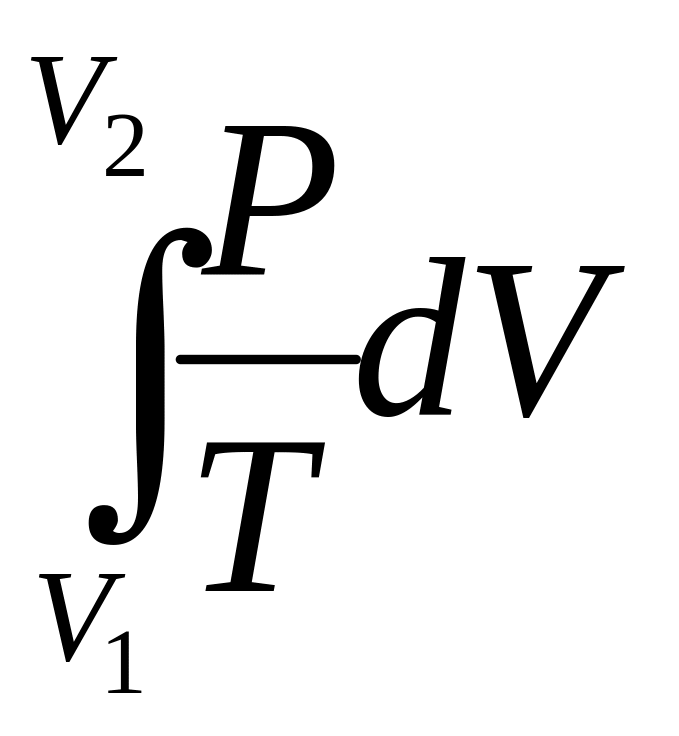+ 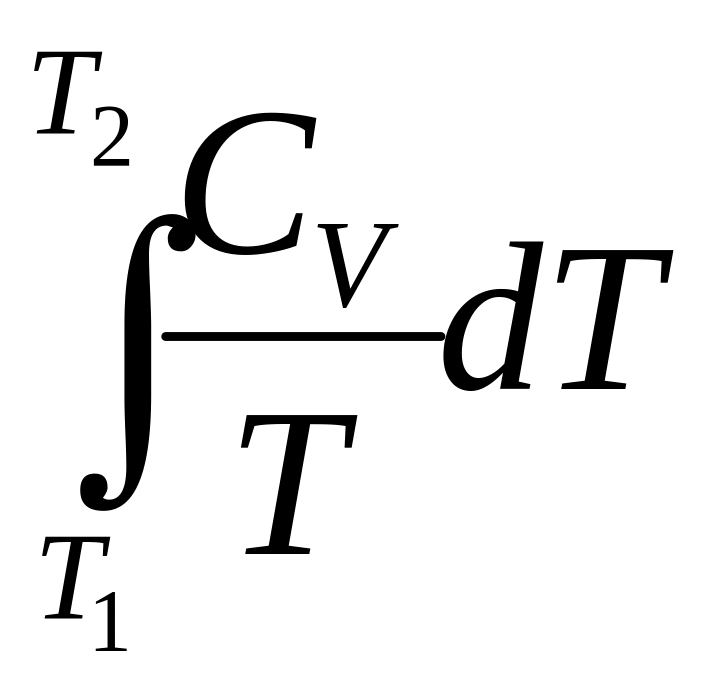= R ln + (II, 4)

S = - 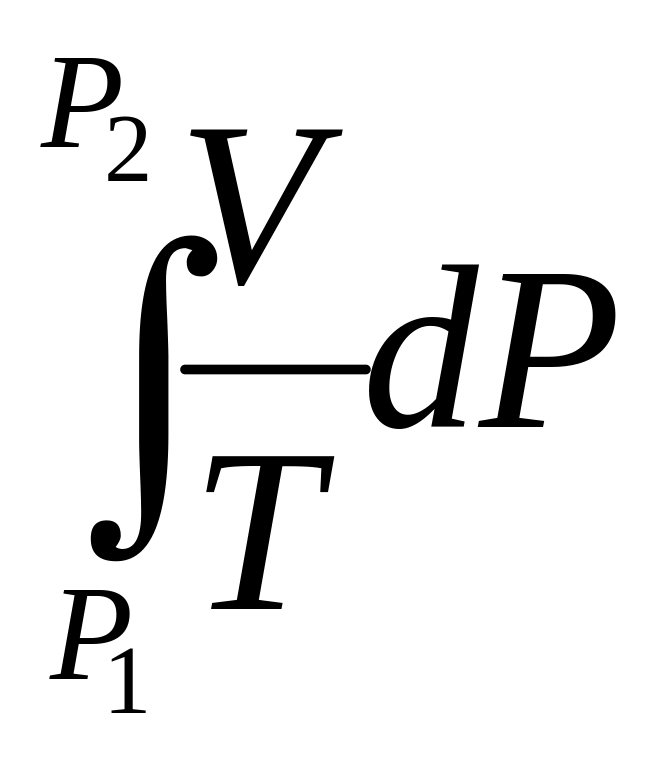+ 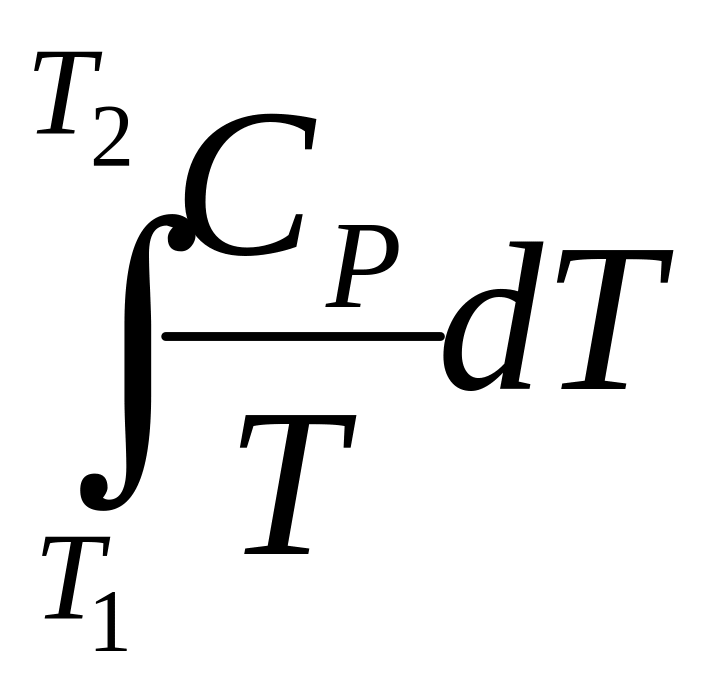= -R ln + C_P ln (II, 4а)

Применим полученные выше соотношения для расчетов изменения энтропии при некоторых процессах:

1. Фазовые превращения (изотермические процессы; Т = const):

S₂ – S₁ = S = = = (II, 5)

Так, например, теплота плавления бензола равна 9,764 кДж/моль; температура плавления t_пл. = 5,5°С. Следовательно, изменение энтропии 1 моль бензола при плавлении (энтропия плавления) равно:

S_пл. = 35,06 Дж/моль

2. Нагревание при постоянном давлении (изобарный процесс; P = const). Из уравнения (III, 18а) получаем:

S = (II, 6)

Найдем изменение энтропии одного моля алюминия при нагревании от 25 до 600 °С. Истинная мольная теплоемкость алюминия может быть выражена уравнением:

С_р= 565,5 + 0,290 Т. По уравнению (II, 4а) изменение энтропии будет равно:

S = = 565,5 2,303 + 0,290(873 – 298) = 608,5 + 166,8 = 775,3 Дж/мольK

§ 4. Постулат Планка. Абсолютные значения энтропии

По уравнению (II, 3) невозможно вычислить абсолютное значение энтропии системы. Такую возможность дает новое, недоказуемое положение, не вытекающее из двух законов термодинамики, которое было сформулировано М.Планком (1912). Согласно этому положению, называемому постулатом Планка, энтропия индивидуального кристаллического вещества при абсолютном нуле равна нулю:

S₀ = 0

Строго говоря, постулат Планка справедлив только для индивидуальных веществ, кристаллы которых идеально построены (в кристаллической решетке все узлы заняты молекулами или атомами, правильно чередующимися и закономерно ориентированными). Такие кристаллы называются идеальными твердыми телами. Реальные кристаллы не являются таковыми, так как их кристаллическая решетка построена не идеально.

Энтропия кристаллической решетки, построенной в некоторой степени беспорядочно, больше энтропии идеально построенной кристаллической решетки. Поэтому реальные кристаллы и при 0 К обладают энтропией, большей нуля. Однако энтропии реальных хорошо образованных кристаллов индивидуальных веществ при абсолютном нуле невелики.

В соответствии с постулатом Планка уравнение (II, 6) для идеального твердого тела примет вид:

= (II, 7)

Постулат Планка используется при термодинамическом исследовании химических процессов для вычисления абсолютных значений энтропии химических соединений - величин, которые имеют большое значение при расчете химических равновесий.

Энтропия широко используется в технической термодинамике (теплотехнике), как один из важных параметров рабочего тела в тепловой машине, например, водяного пара. Величины энтропии водяного пара в данном состоянии вычисляются по сравнению с некоторым стандартным состоянием - обычно 0°С и 1 amм. Эти значения энтропии используются для построения так называемых энтропийных диаграмм состояния водяного пара в координатах S—Т или S—H (диаграмма Молье). В таких диаграммах подобно диаграммам V—P, можно изображать различные процессы, протекающие в рабочем теле тепловой машины и составляющие рабочие циклы машины.

В заключение следует отметить, что нам не придется углубляться в область термодинамики. Наша цель лишь проиллюстрировать основные идеи этой науки и объяснить причины, по которым возможно основываться на ее аргументах.

Наконец, два закона термодинамики часто формулируют так:

Первый закон: Энергия Вселенной всегда постоянна.

Второй закон: Энтропия Вселенной всегда возрастает.

Несмотря на некоторые недостатки приведенных выше формулировок обоих законов, они легко запоминаются и дают представление, о чем собственно идет речь.

Напомним, что второй закон термодинамики определяет критерии самопроизвольного протекания процессов в изолированных системах. Однако подобные условия (отсутствие обмена энергией и веществом с окружающей средой) реализуются сравнительно редко. Поэтому представляется важным сформулировать подобного рода критерии для закрытых систем, где возможен обмен энергией с окружающей средой. Для этого нам потребуется определить две новые функции состояния – энергию Гельмгольца и энергию Гиббса.