МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КАФЕДРА ВЫСШЕЙ И ПРИКЛАДНОЙ МАТЕМАТИКИ

Математическая статистика Методические указания и индивидуальные задания к лабораторным работам по курсу «Математическая статистика »

КУРСК 2013

Составители: В.В. Жилин, В.В. Ефремов

УДК 519.2

Математическая статистика: Методические указания и индивидуальные задания к лабораторным работам по курсу «Математическая статистика »./ Курск. гос. техн. ун-т; Сост.: В.В. Жилин, В.В. Ефремов. Курск, 2013. 46 с.

Предлагаются индивидуальные задания к лабораторным работам по курсу «Математическая статистика » с примерами их выполнения.

Предназначены для студентов всех специальностей.

Текст печатается в авторской редакции

ЛР № 020280 от 09.12.96. ПЛД № 50-25 от 01.04.97

Подписано в печать .Формат 60Х84 1/16 . Печать офсетная. Усл.печ.л. . Уч.-изд.л. .

Тираж 100 экз. Заказ . Бесплатно.

Курский государственный технический университет.

Подразделение оперативной полиграфии Курского государственного технического университета.

Адрес университета и подразделения оперативной полиграфии:

305039, Курск, ул. 50 лет Октября, 94.

Расчетная работа №1 выборочный метод оценки качества партии товара

Поступили пробные партии товаров, размером , где ВО – максимально допустимое верхнее отклонение размера, НО – максимально допустимое нижнее отклонение. Из каждой партии взята выборка, объема n штук. Товар из выборки измерены прибором с ценой деления <0,1∙2d, где 2d=ВО-НО – допуск, и результаты измерения x_i сведены в таблицу.

Необходимо определить наиболее соответствующую требованиям партию, применив следующие критерии оценки:

0. Оценка мат. ожидания 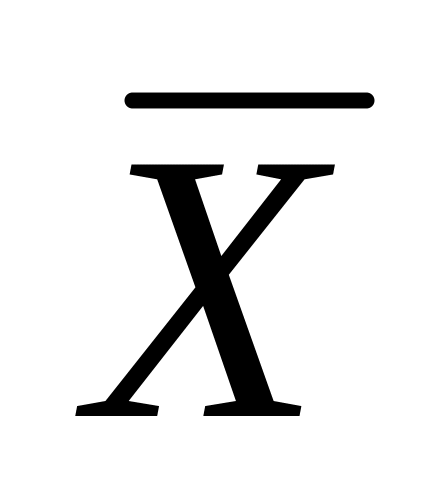наиболее близка к требуемому размеру D.

1. Разброс параметров товара (среднеквадратическое отклонение) минимально.

2. Вероятность выхода из интервала допустимых отклонений минимальна.

Порядок выполнения работы

1. По результатам составляется таблица распределения размеров деталей выборки.

а) Цена разряда c=(x_max-x_min)/m, x_max – максимальное наблюденное значение, x_min – минимальное наблюденное значение, m – число интервалов, m=1+3,322lg(n). Проверить, с>0,1∙2d. В случае необходимости пересчитать для меньшего числа интервалов;

б) Подсчитать частоты f_i и относительные частоты m_i=f_i/n наблюденных значений по интервалам.

2. Считая, что выборка извлечена из нормально распределенной генеральной совокупности, рассчитать параметры статистического распределения:

а) , , при n>30, , при n<30. За x_i принимается середина разряда;

б) Определить значение σ=(1+q)s, q – коэффициент, определяющий границу доверительного интервала нахождения генеральной дисперсии распределения по найденному выборочному среднеквадратическому отклонению s, q взять из таблицы 4 [3] в зависимости от n;

в) Построить гистограмму распределения наблюденных значений. Отметить на ней D, ВО, НО, и трехсигмовые. пределы. Сделать предварительные выводы о качестве партий товара.

3. Определить вероятность получения брака.

а) Смещение оценки математического ожидания от требуемого размера. | -D|;

б) Вероятный процент брака q=[0,5-Ф((d-(| -D |))/σ)]∙100%.

4. Сделать вывод о выборе партии с наилучшими показателями.