Тема 2. Теоретические основы реологии пищевых масс

2.1 Основные понятия и определения

Любое внешнее воздействие на тело приводит либо к его перемещению как целого, либо к изменению его первоначальной формы, либо к наложению этих эффектов. Перемещение тела как целого, без изменения его формы (движение в пространстве, вращение вокруг центра тяжести) составляет предмет механики.

Центральными понятиями механики сплошных сред, на которой базируется реология, являются понятия напряжения и деформации. При этом с точки зрения механики интерес представляет только то, что происходит внутри тела. Реология занимается свойствами вещества, трактуя эти свойства как соотношение между напряжениями и деформациями.

Реология — наука о деформациях и текучести сплошных сред, обнаруживающих упругие, пластические и вязкие свойства в различных сочетаниях.

Приложенные к телу внешние силы создают динамическую ситуацию в любой точке тела, которая характеризуется напряжением. Напряжения действуют внутри вещества и определяются силами, приложенными к телу безотносительно породы и причины происхождения этих сил. В некоторых случаях напряжения могут возникать внутри тела и в отсутствие внешних сил (например, в случае неоднородности температурного поля).

Напряжение - мера внутренних сил F [Н], возникающих в теле под влиянием внешних воздействий на единицу площади А [м²], нормальной к вектору приложения силы:

s = F/A, Па

Напряжения могут быть нормальными и касательными - в зависимости от характера приложения силы.

Только нормальные напряжения могут вызвать изменения объёма тела, в то время как касательные напряжения изменяют его форму.

Случай напряжённого состояния, когда объект подвергается действию всестороннего давления, называют гидростатическим давлением.

Гидростатическое давление - отношение силы, равномерно распределенной по нормальной к ней поверхности, к площади этой поверхности.

Основной особенностью гидростатического давления является отсутствие касательных напряжений, то есть все главные напряжения в теле, находящемся под действием гидростатического давления, равны между собой:

Si = S = S3 = -p.

В данном равенстве знак «-» означает, что сила направлена внутрь каждого элемента объёма тела.

Распределение напряжений в теле описывается уравнениями равновесия (балансовыми уравнениями) Навье, Пуассона и Коши. В сущности, эти уравнения представляют собой выражение второго закона Ньютона: сумма всех сил, действующих на тело в состоянии равновесия, равно нулю.

Явление деформации можно интерпретировать с геометрической точки зрения: изменение формы тела по сути своей представляется изменением расстояния между различными точками в объёме тела.

Деформация - это изменение формы и (или) линейных размеров тела под действием внешних сил, при изменении влажности, температуры и др., при котором частицы или молекулы смещаются одна относительно другой без нарушения сплошности тела.

Деформацию как изменение расстояния между двумя точками можно описать, рассматривая перемещение в пространстве двух соседних точек, отстоящих друг от друга на бесконечно малое расстояние.

Пусть начальное расстояние между точками А и В в материале равняется dS. Вследствие каких либо причин точки меняют своё положение на А' и B'. Их перемещение в пространстве не представляет интереса для механики сплошных сред, но вот изменение расстояния между ними с dS до dS' имеет значение. Более того: важна не абсолютная величина (dS'- dS), а относительное изменение между ними, выражающееся следующим образом:

e = (dS'- dS)/ dS.

Поскольку исходное расстояние между точками А и В в материале было бесконечно малым, а после деформации не возникает разрывов - принимаем, что расстояние между точками А' и B' также бесконечно мало.

Таким образом, если рассматривать деформацию как относительное

смещение частей или частиц тела без нарушения его непрерывности, становится

возможным использование математического аппарата бесконечно малых величин,

16

дифференциальное и интегральное исчисление, а также оперировать равномерно ограниченными непрерывными функциями.

С позиции геометрической интерпретации выделяют малые деформации (между точками, бесконечно мало удалёнными друг от друга) и большие (конечные) деформации.

При обсуждении концепции больших деформаций принимается, что существует некое начальное состояние тела, по отношению к которому вычисляется деформация. Именно в этом смысле течение жидкости не связывается с какой-либо деформацией, поскольку все её состояния эквивалентны. Так что только для материалов, обладающих «памятью» о своём исходном состоянии, можно говорить о деформации по отношению к этому исходному состоянию.

Величина и характер деформации зависят от способа приложения внешних сил, свойств материала тела и его формы.

Деформация проявляется в виде:

а) обратимых (упругих) деформаций, которые возникают в теле при приложении нагрузки и исчезают, если нагрузки снять;

б) пластических (вязких) деформаций, которые появляются только в том случае, когда вызванные нагрузкой напряжения превышают известную величину

• предел текучести; они сохраняется после снятия нагрузки;

в) вязкого течения, которое возникает при любых сколь угодно малых (отличных от нуля) нагрузках; при этом скорость деформаций растёт с увеличением нагрузки.

Многие пищевые материалы по мере роста нагрузок проявляют все перечисленные виды деформаций: вначале деформируются упруго, затем начинают пластически течь и при дальнейшем росте нагрузок текут вязко.

Еще одно свойство, которым могут обладать среды, изучаемые реологией,

• это высокоэластичность, характерная, например, для резины, когда материал допускает десятикратное растяжение, а после снятия нагрузки практически мгновенно восстанавливает первоначальное состояние.

Кроме того, существует и другое деление деформаций. Например, по виду нагружения они могут быть сдвиговыми (рис. 1а), одноосными (линейными) (рис. 1б), а так же двухосными (плоскими) и объёмными.

а) сдвиг; б) растяжение Рисунок 1 - Схемы нагружения материалов

При этом деформации вычисляются по уравнениям:

g= D/a, e = Dl/l.

Сдвиг - очень важный вид деформации в реологии.

Случай простого сдвига - скольжение соседних слоёв материала относительно друг друга. Он рассматривается как плоская деформация, параллельная неподвижной плоскости вследствие действия на гранях элемента касательных напряжений. Простой сдвиг представляет собой случай ламинарного потока, при котором тело можно считать состоящим из бесконечно тонких слоёв. Эти слои не деформируются, а скользят один по другому. Также простой сдвиг может осуществляться при некоторых схемах деформирования твёрдых тел, например при кручении длинных труб или проволоки.

Другая разновидность сдвига - двумерный, плоский, «чистый» сдвиг, при котором не происходит поворота линейных элементов тела, а только их параллельный перенос и изменение линейных размеров.

При сдвиговых деформациях изменений объёма тела не происходит.

При простом сдвиге происходит не только изменение длины линейных элементов (вдоль направления главных осей), но также их повороты (рис. 2).

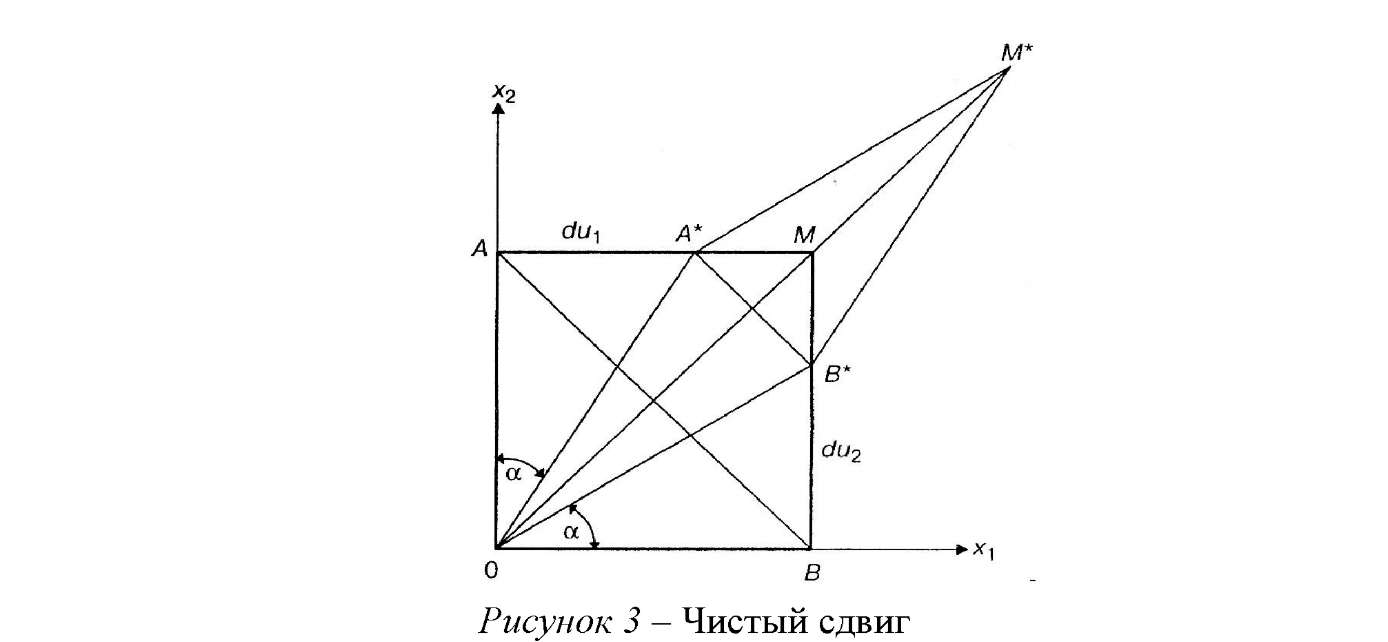
Геометрическое представление плоского (чистого) сдвига показано на рис. 3. При чистом сдвиге диагональ АВ маленького квадрата (в данной точке) перемещается вследствие деформации в новое положение А*В*, параллельное первоначальному; а диагональ ОМ вообще положения своего не меняет - только растягивается до величины ОМ*. Таким образом, ни один элемент тела не претерпевает вращения. Очевидно, что превращение квадрата ОАМВ в ромб ОА*М*В* может быть осуществлено сжатием исходного квадрата вдоль направления АВ с одновременным растяжением вдоль направления ОМ. Это означает, что простой сдвиг может рассматриваться как комбинация двух деформаций одноосного растяжения.

А А*

/ / J	*2 —' "С- — - ^
0		а;
	f
	-J—¥У

б)

а) малые; б) большие Рисунок 2 - Деформации при простом сдвиге

Таким образом, различие между простым и чистым сдвигом такое же, как между деформацией и смещением. Это различие существенно при формулировке уравнений, описывающих реологические свойства реальных материалов.

При одноосном растяжении образец (нить, стержень) претерпевает изменения не только в продольном, но и в поперечном направлении. Связь между изменением размеров в обоих направлениях отражает внутренние свойства материала и может быть установлена, исходя из простых геометрических соображений.

При одноосном растяжении поперечные размеры тела уменьшаются. Отношение изменений поперечного и продольного размеров называется коэффициентом Пуассона, который представляет собой внутреннюю характеристику свойств материала.

m = e/e,

где £r - относительная поперечная деформация; e - относительная продольная деформация.

При сжатии пластично-вязких тел, не заключённых в жёсткую форму, наряду с упругими возможны необратимые пластические деформации, связанные с уменьшением объёма.

Тогда объёмная деформация ev будет представлять собой отношение изменения объёма тела DV = V - Vkк его первоначальному объёму V:

ev=DV/V,

где V - начальный объём, м²;

Vk - объём тела после деформации, м².

При одноосном сжатии реализуется условие постоянства объёма: уменьшается высота тела и увеличиваются его поперечные размеры, что также характеризуется относительными деформациями, которые также количественно связаны между собой посредством коэффициента Пуассона.

Принято считать, что коэффициент Пуассона является также мерой объёмных изменений при малых деформациях. При m = 0,5 деформация происходит без изменения объёмов тела. Для реальных твёрдых тел m < 0,5. В большинстве случаев значение коэффициента Пуассона лежит в диапазоне m = 0,3 - 0,35. Это означает, что одноосное растяжение сопровождается увеличением объёма тела. Без изменения объёма, с величиной m @ 0,5 деформируются только резины.

Коэффициент Пуассона не может быть больше 0,5, так как в противном случае гидростатическое сжатие вызывало бы увеличение объёма (абсурдно с позиций физики). В то же время значения коэффициента могут быть отрицательны: в этих случаях при одноосном растяжении поперечные размеры образца увеличиваются, что характерно для пен.

Если деформация при сдвиге под действием конечных сил увеличивается непрерывно и постоянно, то материал начинает течь. При этом вектор скорости всех точек тела одинаков: присутствует движение, деформация отсутствует. Ус­тановившийся режим течения характеризуется градиентом скорости, который по смыслу аналогичен скорости деформации.

Деформация проявляется тогда, когда имеет место градиент скорости «в точке». Это означает, что соседние точки (с бесконечно малым расстоянием между ними) движутся с разными скоростями.

В области больших деформаций скорость вычислить сложнее, поскольку положение деформируемых элементов тела непрерывно изменяется во времени. Таким образом, при неустановившемся процессе учитывают скорость деформации (градиент скорости); при установившемся процессе деформирования изменение деформации в единицу времени постоянно. Все это описывается понятием «скорость деформации» при растяжении - сжатии e' и при сдвиге g.

e' = de/dt, g = dgdt

При математическом описании больших деформаций используют специальные меры деформации.

Таким образом, можно сказать, что типичный реологический процесс представляет собой сравнительно медленное течение вещества, в котором обнаруживаются упругие, пластические или высокоэластические свойства.