Определение токов в схеме с помощью метода эквивалентных преобразований

R₁=R₂=1Ом

R₃=R₄=2Ом

R₅=4Ом

E=16В

I, I_1, I₂ - ?

Решение

Анализ

l =3, k=2, m=3

N_I=2-1=1

a: I=I₁+I₂

b: I₁+I₂= I

N_J=0, N_E=0

N_II=3-1-0=2

m= N_I+ N_II

пр.ч= N_I+ N_II=1+2=3

л.ч=пр.ч – первая минипроверка

N_МКТ= N_II=2

N_МУП= N_I-N_E=1-0=1

Формально можно считать, что эту схему лучше всего решать методом узловых потенциалов, в частности методом двух узлов.

Если рассматриваемая схема содержит один источник энергии, то ее наиболее рационально решать, используя следующие два метода:

1. Метод эквивалентных преобразований (МЭП);

2. Метод пропорциональных величин (МПВ);

Занятие №3

a: I=I₁+I₂

b1a2b: I₁R₁+I₁R₂+ I₂R₃+I₂R₄=E

a3b2a: : I₃R₅-I₂R₄-I₂R₃=0

Матричная форма

1· I₁-1· I₂-1· I₃=0

(R₁+R₂)· I₁+(R₃+R₄)· I₂+0· I₃=E

0· I₁-(R₃+R₄)· I₂+R₅· I₅=0

[A] - квадратная матрица коэффициент при неизвестных;

[I ] - матрица-столбец неизвестных токов;

[B] - матрица-столбец известных источников

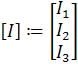
Используя метод Крамера:

=1

Метод эквивалентных преобразований

R₁ = R₂ = R₃ = R₄ = 1 Ом, R₅ = 2 Ом, E = 12 B

I - ?

1. Анализ

2. R_экв1 = R₁ + R₂ = 1+1 = 2 Ом

R _экв2 = R₃ + R₄ = 1+1 = 2 Ом

Так как R_экв2 и R₅ подключены к двум одноименным узлам a и b, то они включены параллельно, и, следовательно, на каждом из них падает одинаковое напряжение!!!

G_экв3 = G_экв2 + G₅

R_экв = R_экв1 + R_экв3 = 2+ 1 = 3 Ом

Для Сх 4 по II закону Кирхгофа

I₁R_экв = E

В данном случае II закон Кирхгофа вырождается в закон Ома.

Напряжение U_ab в Сх 2 и Сх3 одинаковы

Из Сх. 3 U_ab = I₁R_экв3 = 4·1=4 В

Из Сх. 2 I₂ =

I₃ =

Первая минипроверка

Для схемы 1, для узла b запишем Iзакон Кирхгофа.

Окончательная проверка производится с помощью проверки мощностей.

Окончательная проверка производится с помощью баланса мощностей.

Занятие №4 Баланс мощностей

Баланс мощностей – интерпретация закона сохранения энергии. Он является заключительным этапом решения любой задачи, т.к. позволяет проверить правильность вычисленных токов.

Формулировка: Мощности, отдаваемые источниками равны мощностям потребленными нагрузкой.

P_ист= P_потр (1)

P_ист= P_E + P_J (2) P_E=∑EI (3) P_J =∑JU_ab (4) P_ист=∑EI+ ∑JU_ab (5)

P_E=∑EI Слагаемые этой суммы берутся со знаком + в том случае, если направление ЭДС и тока совпадают, в противном случае со знаком –

Мощность, отдаваемая источником тока (P_J) определяется по уравнению (4)

P = UI (6) dim p = Вт

Согласно закону Ома U = IR (7)

Подставим 7 в 6 P = I²R (8)

I = (9)

Подставим 9 в 6 P = (10)

(11)

Подставим 11 в 10 P = U²G (12)

При определении мощности в резисторе можно использовать любую формулу из полученных— 6, 8, 10, 12.

P _потр=∑I²R – арифметическая сумма мощностей выделяемая нагрузкой. Кроме того вычисление мощности на каждом резисторе помогает правильному выбору номинала резистора.

P_ист = P_потр

P_ист = EI₁ = 12 · 4 = 48 Вт

P_потр = Вт

Левая часть = правой части

Т.к. баланс соблюдается, то токи определены верно.