Расчет параметров разноритмичных потоков с использованием матриц

К параметрам потока относятся: n - количество частных или специализированных потоков; т - число изделий; t - продолжительности функционирования потоков на изделии; tpi - периоды включения потоков; Т - продолжительность потока; - продолжительности функционирования частных потоков; toi - продолжительности перерывов между работами на отдельных частных потоках; С - степень использования потоками фронта работ.

Большинство этих параметров можно установить или рассчитать с использованием информации о конкретных изделиях, (объемы и трудоемкость каждого вида работ и др.). Такие параметры, как продолжительность функционирования потока, периоды (время) их включения, очередность, целесообразно рассчитывать с использованием матриц.

Особенности расчетов с использованием матриц рассмотрим на конкретных примерах. Определим параметры разноритмичных потоков на примере потока, информация о котором задана следующей исходной таблицей (табл. 9).

Таблица 9.

Продолжительность функционирования потоков на изделиях

Изделия	Номер потока
	1	2	3	4
I	2	3	1	2
II	2	3	1	2
III	2	3	1	2
IV	2	3	1	2

Расчет продолжительности и других параметров потока с использованием матриц рекомендуется выполнять в следующем порядке. В середину клеток матрицы, приведенной на рис. 29, записывают продолжительности операций на изделиях. Сначала в конце каждой графы проставляют продолжительность потоков , для чего суммируют продолжительности операций на всех изделиях. Так для 1-го потока эта продолжительность равна 8 единицам времени, для 2-го – 12 единицам времени и т.д. Далее, в верхний левый угол первой клетки заносят время начала 1-го потока на 1-м изделии (обычно нуль), а в нижний правый угол — окончание работы потока, которое равно времени начала работы плюс ее продолжительность. Так как время окончания работы на I-м изделии считается началом работы потока на 2-м, то оно без изменений переносится в левый верхний угол второй клетки этой же графы (см. рис. 33). Суммируя это время с продолжительностью работы на 2-м изделии, определяют время окончания работы. Это время записывают в нижний правый угол второй клетки. Таким образом, рассчитывают начала и окончания работ 1-го потока на всех изделиях. Если продолжительность последующего потока больше продолжительности предыдущего, то расчет ведут сверху вниз, а если меньше, то снизу вверх. Так как общая продолжительность 2-го потока больше продолжительности работ 1-го (12>8), то расчет начал и окончаний 2-го потока начинают сверху, то есть с момента, когда освободится I-е изделие. Для этого из нижнего угла первой клетки первой графы время, характеризующее окончания работ на I-м изделии, переносят в левый верхний угол первой клетки второй графы. Далее расчет аналогичен предыдущему.

		Потоки												∑t j
		1			2			3			4			∑t j+∑t 0
Изделия	I	0			2			11			12
			2		0	3		6	1		0	2			8/14
				2			5			12			14
	II	2			5			12			14
			2		1	3		4	1		1	2			8/14
				4			8			13			16
	III	4			8			13			16
			2		2	3		2	1		2	2			814
				6			11			14			18
	IV	6			11			14			18
			2		3	3		0	1		3	2			8/14
				8			14			15			20
∑t j		8			12			4			8			C=32/56 =0,57
∑t 0			6			12			6

Рис. 29. Матрица с результатами расчета разноритмичного потока

Так как продолжительность 3-го потока меньше продолжительности работы 2-го (4<12), то расчет начал и окончаний работ 3-го потока следует вести снизу вверх. Аналогичным образом заполняют все клетки матрицы. Цифра в нижнем углу последней клетки матрицы показывает общую продолжительность выполнения комплекса работ. После расчетов параметров потока целесообразно построить циклограмму потока (рис. 30).

Рис. 30. Циклограмма разноритмичного потока, рассчитанного с использованием матрицы

Расчет параметров неритмичных потоков с использованием матриц аналогичен расчету разноритмичных, за исключением того, что в процессе расчетов необходимо определять для каждой пары смежных потоков место их критического сближения.

В качестве примера рассчитаем параметры неритмичного потока, информация о котором представлена в матрице (рис. 31). Первоначально определяют места критических сближений каждой пары смежных потоков. Результаты записывают в последнюю строку матрицы в виде столбца. В данном примере наибольшее значение из полученных сумм равно 10. Это значит, что критическое сближение двух рассматриваемых потоков находится на I и II изделиях. Аналогично находят места критических сближений всех других потоков. После определения мест критических сближений расчет начинают с тех клеток матрицы, на которых установлено критическое сближение.

Циклограмма неритмичного потока, рассчитанного на матрице (рис. 29), приведена на рис. 32.

Оценку качества запроектированных потоков производят с использованием различных критериев, к которым относятся: продолжительность потока; степень совмещения работ; уровень ритмичности потребления ресурсов; уровень равномерности.

Критерий продолжительности является важнейшим, так как продолжительность оказывает влияние на эффективность производства работ.

		Потоки								∑t j
			∑t j+∑t 0	2		3		4		∑t j+∑t 0
		0		3		6		8
	1	3		0 1		2	1	1 1		6/9			2
			3	4			7	9
Объек-		3		4		7		9
ты	2	1		0 2		1 2		0 1					0
			4	6			S	10		6/7
		4		6		9		10
	3	1		1 2		1	1	0 3		7/9			-2
			5	8			10	13
		5		8		10		13
	4	1		2 2		0	2	1 1		6/9			0
			6	.10			12	14
∑t j		6		7			6	. 6		C=2 5/34
∑t 0			3		4		2			= 0,735
			10		7		7
			10		8		8
			9		8		8
				8		9		7

Рис. 31. Матрица с результатами расчета неритмичного потока

Рис. 32. Циклограмма неритмичного потока, рассчитанного с использованием матрицы

Продолжительность потока зависит среди прочего также от очередности включения в процессы изделий. Полный перебор всех возможных вариантов включения в процесс изделий, при котором продолжительность потока минимальна, практически нереальная задача, так как число вариантов достигает огромных величин. Поэтому при организации неритмичных потоков возникает задача в разработке алгоритма направленного перебора очередностей включения в процесс изделий.

Сущность его заключается в минимизации периода развертывания потока, состоящего из двух частных за счет перехода от случайной очередности включения изделий в процесс к упорядоченной. Упорядоченная очередность достигается тем, что изделия для 1-го частного потока располагают в матрице по возрастанию продолжительности операций, а для 2-го — по убыванию. Операция повторяется со следующими строками исходной матрицы до полного ее перестроения. Рассмотренный алгоритм минимизирует продолжительность потоков, состоящих лишь из двух частных, однако такие потоки встречаются редко. Для потоков, состоящих из более двух потоков, разработан алгоритм, основанный на так называемом методе ветвей и границ. Сущность алгоритма заключается в направленном переборе вариантов последовательности изготовления изделий. Наряду с обоснованным методом направленного перебора очередности освоения частных потоков имеются методы, которые носят эвристический характер. Эти методы в некоторых случаях позволяют получить решение, близкое к варианту с минимальной продолжительностью. Один из таких методов сводится к тому, что в начале рассчитывают ряд показателей, которые используют далее для построения матрицы с минимальной продолжительностью. К таким показателям относятся: суммарные продолжительности специализированных потоков до ( ) и после ( ) ведущего частного потока (в качестве ведущего частного потока принимают поток, имеющий наибольшую продолжительность) и разности ( ) времени работ на каждом изделии первого и последнего частных потоков. Эти показатели, подсчитываемые по данным матрицы, сводят в ее последние графы. Для рассмотренного неритмичного потока (см. рис.32) ведущими является 2-й поток, так как его продолжительность наибольшая (7>6). Подсчитанные показатели сведены в две последние графы матрицы. В первую строку матрицы записывают номер изделия, в котором суммарная продолжительность потоков, предшествующих ведущему потоку ( ), минимальная. В последнюю строку записывается номер изделия с наименьшим значением суммарной продолжительности работ после ведущего потока ( ). Затем заполняется вторая и предпоследние строки новой матрицы таким образом, чтобы значения и увеличивались по мере приближения к середине матрицы (рис.31).

В данном примере новая продолжительность потока составила 12 единиц времени, что на 2 единицы меньше продолжительности потока с первоначальной очередностью. После этого формируют матрицу по второму показателю — разнице ритмов работ первого и последнего потоков. Для этого в первую строку матрицы записывают номер изделия с минимальной разницей ритмов, а далее по мере возрастания численного значения этой

Рис. 33. Матрица, сформированная с использованием показателей и

Рис. 34. Матрица, сформированная с использованием показателя

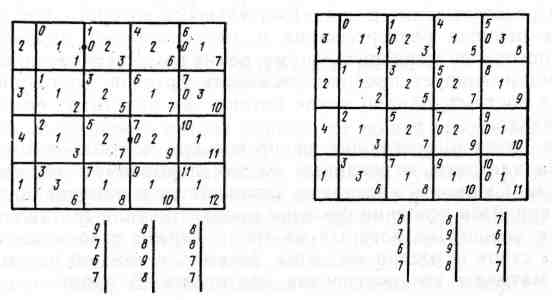
разницы (рис. 34). Полученная матрица рассчитывается. В нашем примере продолжительность потока с новой очередностью составила 11 единиц времени, что меньше на 3 единицы первоначальной продолжительности потока и на 1 единицу продолжительности потока, сформированного по первому показателю.

Окончательно принимается та очередность включения изделий в работу, которая обеспечивает наименьшую продолжительность. На рис. 35 приведена окончательная циклограмма с продолжительностью потока, близкой к минимальной.

Степень совмещения работ на всех изделиях (объектах) оценивают коэффициентом использования времени С:

С =		(10)
	+

Где: — суммарная продолжительность всех потоков на изделиях (участках), дни; — суммарная продолжительность организационных перерывов между потоками, дни.

Суммарное значение организационных перерывов помещают в последнюю строку матрицы, так для матрицы рис. 31 коэффициент использование времени (С)—0,57, для потока на матрице рис.32, значение этого коэффициента - 0,735.

Рис. 35. Циклограмма неритмичного потока после корректировки.

Равномерность ритмичных потоков оценивают показателем равномерности , который подсчитывают по формуле

= (11)

где R — потребность в ресурсах в период стабильного состояния потока; — средняя потребность в ресурсах за время действия потока. Эту формулу можно представить так:

= (12)

где g — трудоемкость всех операций на одном изделии, чел-дн. Подставляя значение Т [см. (4)], получим

β = (13)

Как следует из формулы (13), значение коэффициента всегда меньше единицы. При этом, чем равномернее поток, тем это значение ближе к единице.