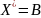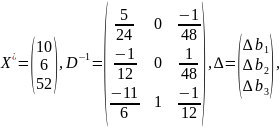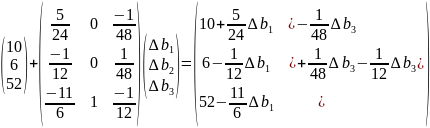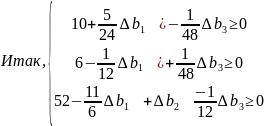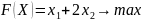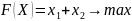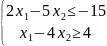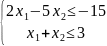- •П.8. Двойственная злп
- •Симметричные двойственные задачи
- •Правила построения дз
- •Пример 19 (построение симметричной дзлп):
- •Пример 17 (построение дзлп):
- •Пример 18 (построение дзлп):
- •Д Базис войственный симплекс-метод
- •Алгоритм двойственного симплекс-метода
- •Свойства двойственных злп
- •Теорема (критерий оптимальности Канторовича): Если для некоторых допустимых решений и двойственных задач выполняется равенство
- •Теорема (малая теорема двойствнности): Для существования оптимального решения любой из пары двойственных задач, необходимо и достаточно существование допустимого решения для каждой из них.
- •П.9.Анализ решения злп
- •Анализ коэффициентов целевой функции
- •Анализ ограничений по ресурсам
- •Анализ ограничений по ресурсам (II способ)
Анализ ограничений по ресурсам (II способ)
Б |
|
30 |
35 |
60 |
65 |
0 |
0 |
0 |
max |
|
|
|
|
|
|
|
B |
||
|
0 |
8 |
|
8 |
|
|
0 |
|
128 |
|
0 |
12 |
|
8 |
6 |
|
1 |
|
220 |
|
0 |
32 |
|
80 |
|
|
0 |
|
800 |
|
- 30 |
-35 |
- 60 |
-65 |
|
0 |
|
660 |
|
Матрица
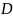 :
: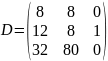
Матрица составлена из столбцов исходной симплекс-таблицы, соответствующих векторам, которые в оптимальном решении задачи вошли в базис.
Б |
|
30 |
35 |
60 |
65 |
0 |
0 |
0 |
max |
|
|
|
|
|
|
|
B |
||
|
30 |
1 |
|
0 |
|
|
0 |
|
1 0 |
|
0 |
0 |
|
0 |
0 |
|
1 |
|
52 |
|
60 |
0 |
|
1 |
|
|
0 |
|
6 |
|
0 |
5 |
0 |
10 |
|
0 |
|
660 |
|
Пусть

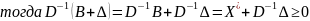
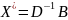
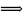 D
D