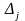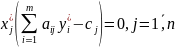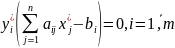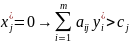Алгоритм двойственного симплекс-метода

1. Находим псевдоплан задачи;

2. Проверяем полученный псевдоплан на оптимальность. Если псевдоплан оптимален, то найдено решение задачи. В противном случае – либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану. Псевдоплан оптимален, если все 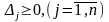и все элементы столбца 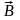неотрицательны;

3. Для определения оптимального плана задачи (если он существует) производят упорядоченный переход от одной симплекс таблицы к другой до тех пор, пока из столбца не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными элементы (m+1)-й строки 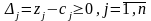. Разрешающую строку выбирают, определяя наибольшее по абсолютной величине отрицательное число столбца (определяется вектор выводимый из базиса). Разрешающий столбец находят определяя наименьшее по абсолютной величине соотношение элементов (m+1)-й строки к соответствующим отрицательным элементам разрешающей строки .

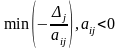4. Находят новый псевдоплан и повторяю алгоритм с пункта 2.

Базис		А1	А2	А3	А4	А5	max
		2	3	0	5	0	В

Пример 20:

А3 А4 А5	0 5 0	2 1 -3	-1 2 2	1 0 0	0 1 0	0 0 1	-12 10 -18
		3	7	0	0	0	50
А3 А4 А1	0 5 2	0 0 1	1/3 8/3 -2/3	1 0 0	0 1 0	2/3 1/3 -1/3	-24 4 6
		0	9	0	0	1	32

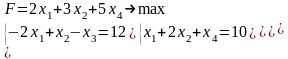
В таблице №1 (-18) – наибольший по модулю отрицательный компонент ; в 3-ей строке таблицы есть элемент , т.е. .

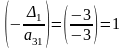Вектор 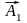вводят в базис вместо 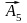, получим псевдоплан

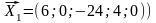
В таблице №2 (во 2 итерации) в столбце есть элемент 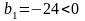, но в первой строке нет элементов меньше 0, следовательно, исходная задача не имеет решения.

Свойства двойственных злп

1. Если задача I имеет решение, то и двойственная ей задача II имеет решение.

2. Если задача I не имеет решения, ввиду ограниченности целевой функции, то задача II не имеет решения ввиду несовместимости системы ограничений.

3. Если задача I имеет альтернативный оптимум, то задача II – вырожденная (в решении имеется имеет базисный ноль).

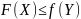4. при всех допустимых .

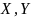5. Если - оптимальные планы пары двойственных задач, то выполняется равенство: .

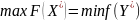6. где 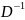– матрица обратная матрице D, столбы которой – векторы условий исходной задачи, образующие базис оптимального решения.

7. 

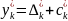
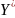8. , выполняются условия «дополняющей нежёсткости»:

что означает:

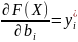9. величина двойственной оценки ресурса показывает насколько возросло бы экстремальное значение целевой функции, если бы объём данного ресурса увеличился на единицу.

соответствие между переменными прямой и двойственной задачи
свободные					базисные
	…		…			…		…
	…		…			…		…
	…		…			…		…
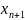
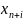
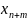
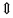
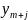
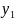
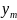
базисные					свободные

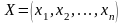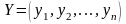Теорема (основное неравенство теории двойственности): Пусть пара двойственных задач (А и В). Для любых допустимых решений и прямоё и двойственной ЗЛП справедливо равенство:

Для любого допустимого плана производства X и любого допустимого вектора оценок ресурсов Y и общая созданная стоимость не превосходит суммарной оценки ресурсов.