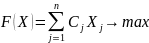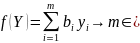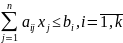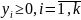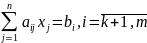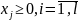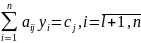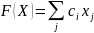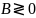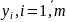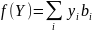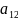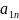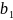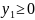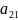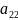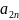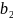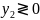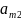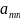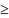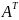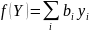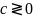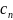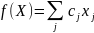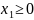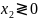- •П.8. Двойственная злп
- •Симметричные двойственные задачи
- •Правила построения дз
- •Пример 19 (построение симметричной дзлп):
- •Пример 17 (построение дзлп):
- •Пример 18 (построение дзлп):
- •Д Базис войственный симплекс-метод
- •Алгоритм двойственного симплекс-метода
- •Свойства двойственных злп
- •Теорема (критерий оптимальности Канторовича): Если для некоторых допустимых решений и двойственных задач выполняется равенство
- •Теорема (малая теорема двойствнности): Для существования оптимального решения любой из пары двойственных задач, необходимо и достаточно существование допустимого решения для каждой из них.
- •П.9.Анализ решения злп
- •Анализ коэффициентов целевой функции
- •Анализ ограничений по ресурсам
- •Анализ ограничений по ресурсам (II способ)
П.8. Двойственная злп
Двойственная задача линейного программирования – это вспомогательная ЗЛП, формулируемая с помощью специальных правил из условий исходной, прямой задачи. Понятие двойственности исключительно важно в теоретическом отношении, но интересно и для практики, так как используется для анализа модели на чувствительность.
Пример 15 (формулировка двойственной ЗЛП):
На
кондитерской фабрике весь ассортимент
выпускаемой карамели разделен на три
однородные группы
 ,
,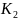 ,
,
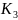 .
Расход основного сырья и его запасы
указаны в таблице 1:
.
Расход основного сырья и его запасы
указаны в таблице 1:
Виды сырья |
Расход сырья на 1 т |
Запас сырья |
|||
|
|
. |
|||
Сахарный песок (I) |
0,7 |
0,7 |
0,7 |
700 |
|
Патока (II) |
0,3 |
0,3 |
0,2 |
300 |
|
Фруктовое пюре (III) |
0 |
0,2 |
0,3 |
150 |
|
Прибыль |
100 |
110 |
120 |
- |
|
Таблица 1.
Другие виды сырья, используемые в небольших количествах не учитываются. В качестве критерия оптимальности плана принимается максимум прибыли.
Пусть (х1, х2, х3) – план выпуска карамели групп , , . F(х) – суммарная прибыль. Математическая модель прямой задачи (1):
max F(х)=100 х1+110 х2+120 х3
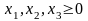
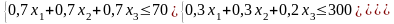 (1)
(1)
Предположим, что принятие решения о продаже сырья потребовало установить цены на основные его виды. Пусть (у1, у2, у3) – цены на сахарный песок, патоку и фруктовое пюре.
Цены устанавливаются исходя из требований:
- общую стоимость сырью покупающая организация стремится минимизировать;
- предприятие согласно продать сырье только по таким ценам, по которым оно получит выручку, не меньше той суммы, которую оно могло бы получить, используя его в собственном производстве.
Эти требования можно сформулировать в виде задачи (2):
|
|
Задачи (1) и (2) называются парой взаимодвойственных ЗЛП. Они заданы в симметричной форме, поэтому являются симметричными двойственными задачами. Переменные у1, у2, у3 - это двойственные, объективно обусловленные оценки. Пара взаимно двойственных задач может быть экономически интерпретирована так:
1.
Сколько и какой продукции
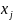 (
(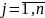 )
надо произвести, чтобы при заданных
стоимостях единицы продукции
)
надо произвести, чтобы при заданных
стоимостях единицы продукции
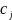 (
)
и объемах имеющихся ресурсов
(
)
и объемах имеющихся ресурсов
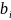 (
(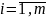 )
и нормах расхода
)
и нормах расхода
 максимизировать выпуск продукции в
стоимостном выражении?
максимизировать выпуск продукции в
стоимостном выражении?
2.
Какова должна быть оценка единицы
каждого из ресурсов
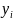 (
),
чтобы при заданных
,
и
минимизировать
общую оценку затрат на все ресурсы.
(
),
чтобы при заданных
,
и
минимизировать
общую оценку затрат на все ресурсы.
Симметричные двойственные задачи
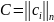

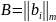




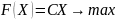 (I)
(I)
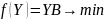 (II)
(II)
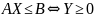

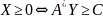
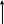
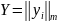
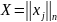
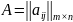
Рисунок 8. Схема построения взаимно-двойственных задач.
Правила построения дз
Каждому i-му ограничению исходной задачи соответствует переменная уi ДЗ и наоборот – каждому j-му ограничению ДЗ соответствует переменная хj ПЗ;
Матрицы А ограничений ПЗДП и А` (ДЗЛП) взаимно транспонированные, следовательно: строка коэффициентов аij в j – м ограничении ДЗЛП есть столбец коэффициентов при хj в ограничениях ПЗЛП, и наоборот;
Свободные члены ограничений одной из задач являются коэффициентами при соответствующих переменных в целевой функции другой задачи. При этом максимизация меняется на минимизацию и наоборот;
В исходной задаче ограничение неравенства следует записывать со знаком ≤ при максимизации, и со знаком ≥ при минимизации;
каждому i - му ограничению - неравенству исходной задачи соответствует в ДЗ условие не отрицательности (уi ≥ 0), а равенству – переменная уi без ограничений на знак (произвольная, свободная). Наоборот, неотрицательной переменной хj ≥ 0 соответствует в ДЗ j –ое ограничение, а произвольной переменной – равенство.
Соотношение двойственности взаимное, то есть задача, двойственная по отношению к двойственной, совпадает с исходной.
|
|
|
|
|
|
|
|
|
|
|
|
Двойственная задача
|
|
исходная ЗПЛ |
|
двойственные переменные |
||||||||
двойственная ЗЛП |
A |
|
max |
|
|
|||||||
|
|
|
… |
|
≤ |
|
|
|||||
|
|
… |
|
= |
|
|
||||||
… |
… … |
… |
… |
… |
||||||||
|
|
… |
|
≤ |
|
|
||||||
min |
|
= |
… |
|
|
|
||||||
|
|
|
|
… |
|
|
|
|||||
|
|
|
|
… |
|
|
|
|||||
исходные переменные

3 |
4 |
-5 |
A |
2 |
-3 |
7 |
2
B |
1 |
-1 |
4 |
3 |
-3 |
4 |
-1 |
-3 |
2 |
1 |
-3 |
-1 |
С
ример 16: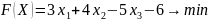 исходная
ЗЛП
исходная
ЗЛП
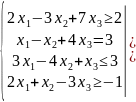
,
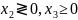
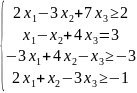



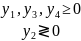
 двойственная
ЗЛП
двойственная
ЗЛП
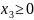

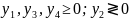

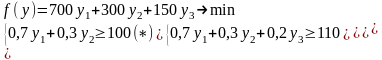 (2)
(2)