Математиканы оқытудың ғылыми таным әдісі. Математикалық зерттеудің негізгі әдістемесіне:

1) байқау және тәжірибе;

2) салыстыру;

3) талдау және біріктіру;

4) жалпылау және арнайы бағытқа салу;

5) абстракциялау және нақтылау сияқты әдістер жатады.

Орта мектепте математиканы үйрену процесі оны оқыту процесімен бірге қарастырылады.

Математиканы оқытудағы бақылау

Адамдарды қоршаған ортаның әр алуан құбылыстары мен жекелген нысандарының қасиеттерімен байланыстарына табиғи жағдайда назар аударып, олардың шын мәніндегі табиғи байланыстарының белгілерін үйренін бақылау әдісі дейміз.

Бақылауды қарапайым қабылдаудан ажырата білу керек. Белгілі бір нысанды қабылдау деп, сол нысанның біздің сезім ағзаларымызға әсер етіп, әсері біздің санамызда тікелей бейнеленуін айтады. Ұзақ мерзімді қабылдауды бақылау дейміз.

Бақылау – есте қалдыру және келесі байқаулардың нәтижесін жинақтаудан тұрады.

Математиканы оқытудағы тәжірибе.

Зерттелетін нысандар мен құбылыстардың табиғи жағдайын өзгертіп, оларға жасанды жағдайлар тұғызуды, жасанды жағдайда оларды басқа нысандармен салыстыруды тәжірибе немесе эксперимент деп атайды. Кез келген эксперимент бақылаумен байланысты. Эксперимент жасаушы эксперименттің барысын яғни тексеріліп отырған нысандармен құбылыстардың жасанды жағдайдағы өзгерісі мен дамуын байқайды. Бұл әдістер эксперименталды ғылымда маңызды рөл атқарады. Математика, жалпы алғанда, эксперименталды ғылым емес, егер қандай да бір қасиет жеке не нақты жағдайларда дұрыс болса, онда оны математик әмбебап әдіс деп есептелмейді.

Сондықтан байқау мен тәжірибе математикада негізгі зерттеу әдісі бола алмайды. Сонымен бірге, байқау мен тәжірибе кейбір математикалық нысандардың қасиетін иллюстрациялауға қолайлы, зертеліп отырған тұжырымның дұрыс-бұрыстығына көз жеткізуге қолайлы. Бұл тұрғыдан алғанда байқау мен тәжірибе математиканы оқытуда зор роль атқарады.

Математиканы оқытуда байқау мен тәжірибені қолдану мысалдары.

Тоғыз жылдық мектептің оқушыларын аудан, периметр, көпбұрыштың тең шамалылығы сияқты ұғымдармен таныстыру үшін, олармен келесі жаттығуларды орындауға болады:

1. берілген фигураның периметрі мен аудандарын салыстыру;

2. фигуралардың периметрлерін және аудандарын салыстыру.

Тәжірибелер мен бақылауларда оқушылар аудандары тең, бірақ периметрлері әртүрлі және периметрлері тең, аудандары әртүрлі көпбұрыш-тарды , тең шамалы фигураларды анықтайды.

Натурал сандардың жай көбейткіштерге жіктелу сипатына қарап және әртүрлі натурал сандарды жай көбейткіштерге жіктеп (тәжірибе жүргізіп), оқушылар жай және құрама сандардын мағынасын анықтайды.

1 = 1; 2 = 2 · 1; 3 = 1 · 3; 4 = 2 · 2 · 1 = 4 · 1;

5 = 5 · 1; 6 = 3 · 2 · 1 = 6 · 1; ...

Бақылау мен тәжірибе жай және құрама санның анықтамасын саналы түрде түсінуге мүмкіндік береді. Мұғалім мен оқушылардың бақылаулар, тәжірибелер жүргізе отырып, тапқан нәтижелерін қатаң, дәл дәлелдеулер деп айтуға болмайды..

Бурбакидің пікірінше, математика – құрылымдарды зерттейтін ғылым. Математикалық құрылымдар базистік және көп еселі болып екіге бөлінеді. Алгебралық, топологиялық құрылымдар және реттеу құрылымдары базистік деп аталынады. Бүкіл математика – осы үш түрлі базистік құрылымдар жиынтығының комбинациясы. Мысалы, группа, сақина, өріс – алгебралық құрылымның түрлері, нақты сандар жиыны мен натурал сандар жиыны реттелген құрылымдардың түрлері, топологиялық кеңістік пен топологиялық-векторлық кеңістік – топологиялық құрылымның белгілі түрі.

Математикалық құрылым деп мынадай жиынды айтамыз:

1. табиғаты кез келген элементтер (мысалы: сан, функция, вектор, матри-цалар);

2. элементтер арасындағы қатынастар;

3. осы қатынастар үшін анықталған белгілі амалдар;

4. амалдардың негізгі қасиеттері аксиомалар жүйесі арқылы көшіріледі.

5-Лекция. Математикалық ұғым

Біздің әрбір сөйлеміміздің сөзі белгілі бір нысандарың тобын анықтайды, құбылыстардың өзара қатынасын бейнелейді. Егер сөз бізге бір заттың басқа бір заттардан айырмашылығы мен көптеген қасиеттерін ерекшелеп көрсетуге көмектессе, ойымызда ол зат ерекшеленіп елестесе не оларға тән ортақ қасиеттер мен байланыстар көрсетілсе, онда ойымыз заттың жалпы қасиеттерін бейнелей алады. Заттар арасындағы құбылыстар мен қатынастардан, олардың нақты қасиеттерінен жалпылап қорытынды шығарылса, бұл олар туралы белгілі бір ұғым болады. Әрбір түсінік сөзбен бірге сәйкес түрленеді, сөз сөйлем туралы түсінікті елестетуге қызмет етеді.

«Ұғым» термині біздің санамызда кейбір нысандарды, шындықтың қатынастары мен процестерді, кейбір заттар сыйпатының бейнесін белгілеу үшін қолданылады. Математикалық ұғым біздің ойымызда белгілі формада нақты жағдайдан абстракцияланған шындыққа көшуді бейнелейді.

Бір зат екінші заттан әр түрлі сапалары мен белгілері, немесе ерекшеліктері арқылы ажыратылады. Әр түрлі нысандардан: жеке қасиеттерді, жалпы қасиеттерді бөліп аламыз.

Нысандар қасиеттерінің адам миында ерекше бейнелену процесін – ұғым деп атайды:

• ұғым жоғары дәрежеде ұйымдасқан материяның жемісі;

• ұғым материалды дүниені бейнелейді;

• ұғым – жалпылау, таным тәсілі ретінде қолданылады;

• ұғым адам қызметінің әрқилылығын білдіреді;

• адам санасына ұғымның қалыптасуы оның тікелей сөз, жазу не символ арқылы өрнектелуінен қалыптаспайды,

• әрбір ұғым өзіне нысандар белгілерін біріктіреді (заттардың қатынасы).

Ұғым мазмұннан және көлемнен тұрады. Ұғым көлемі – осы белгілерге жататын барлық нысандарды білдіреді, ал нысандардың сипаттамалық қасиеті осы ұғымның мазмұны болады. Мысалы, «Үшбұрыш» ұғымы мүмкін болатын барлық үшбұрыштар белгілерін білдіреді. (Мұндағы тікбұрышты, теңбүйірлі, теңқабырғалы үшбұрыш деген түрлері ұғымның көлемі болады және сипаттамалық қасиеттерге: үш қабырғасы, үш төбесі, үш бұрышы жатады (ұғымның мазмұны құралады); «теңдеу» ұғымы – барлық мүмкін болатын теңдеулер белгілерін біріктіреді (көлемі) және сипаттамалық қасиеті – бірнеше айнымалылардан және айнымалылардың әртүрлі дәрежелерінен, сол айнымалылардың әртүрлі функцияларынан тұратын теңдік болады. Басқаша айтқанда, (ұғымның мазмұны) ұғымның мазмұны анықтама арқылы, көлемі – классификациялау жолымен табылады.

Ұғымды қалыптастыру – күрделі психологиялық үдеріс, білім берудің жай танымдық формасы – түйсіну арқылы іске асады.

Сезіну – қабылдау – түсінік – ұғым. Әдетте бұл процесс екі сатыдан тұрады. Сезімдік қабылдау арқылы түсінік пайда болады және логикалық түрде түсініктен ұғымға жалпылау мен абстракцияның көмегі арқылы жетеді. Мысалы, оқушы «үш» санын қалыптастыру үшін:

• алдымен әртүрлі нақты жиындармен танысады, айталық: үш алма, «үшбұрыш», үш аю, үш жапырақ т.с.с.

• бұлардың әртүрлі қасиеттеріне назар аударады.

«Көру» процесі бала санасында бейнелеудің ерекше формасын қабылдайды (сезінеді). Нысанды көру арқылы сезімдік түйсіну – танымның ең алғашқы сатысы. Ол ұғымның сыртқы белгілеріне сәйкес қалыптасады.

Ұғымды тұжырымдау сұлбасын еске түсірелік: қабылдау – сезіну – түсінік – ұғым.

Индуктивтік әдіспен ұғымды ендірудегі оқыту процесінің негізгі кезеңдері:

1. берілген ұғымның қажеттігін көрсететін (қабылдау – сезіну) практикалық мысалдар келтіру;

2. берілген ұғымның маңызды және өте маңызды емес белгілерін анықтайды (оқушылар) және берілген ұғымды белгілейтін термин ендіреді (мұғалім). Ол үшін қабылдаудан (сезіну) түсінікке өтетін өтпелі кезең керек, берілген ұғымды белгілейтін терминнің дәлелі қажет (мұғалім);

3. берілген ұғымның барынша маңызды қасиеттері таңдап алынады және осы ұғымның анықтамасы тұжырымдалады (оқушылар); бұдан соң оған мұғалім дәл анықтама береді, мұны оқушылар қайталайды. Бұл үшін арада түсініктен ұғымға ауысатындай жағдай болуы керек;

4. арнайы бөліп алынатын ұғым нақты мысалдармен көрсетіледі, қарама-қарсы мысалдар келтіріледі және символдық белгілеуі көрсетіледі (оқушы және мұғалім).

Бұл ұғымның пайда болуын білдіреді

Бұдан соң оқушылар басқа ұғымға көшуге болатын, басқа анықтама береді. Бұл ұғымның меңгерілуі болады.

Абстракты-дедукциялық әдіспен оқытудың негізгі кезеңдері:

- алдымен жаңа ұғымға анықтама беріледі, бұл үшін оны белгілеуші термин тұжырымдалады;

- ұғым ендірілген өрнектің жеке және ерекше жағдайлары қарастырылады; қарама-қарсы пікірлерден мысал келтіріледі;

- келесі кезекте ендірілген ұғым нақты мысалдар арқылы иллюстрацияланады;

- соңында ендірілген ұғымды бекіту үшін мысалдар келтіріледі.

Жаңа ұғымның меңгерілуі. Егер ұғым меңгерілген болса, онда:

- оқушының ұғымның көлемі мен мазмұны туралы толық түсінігі болады;

- оқушы математикалық іс-әрекеттің барысында ұғымды қолдана біледі;

- оқушы жаңа жағдайларда өзінің білімі мен тәжірибесін қолданады.

Ұғымның анықтамасын игеру процесінде оқушылар қателіктер жібермеуі үшін, олар: анықталған және анықтаушы белгілерді ажырата білуі керек.

Анықталатын нысанға сәйкес келетін ұғым анықталған ұғым деп аталады. Анықталатын нысан мазмұнын ашуға көмектесетін ұғым анықтаушы ұғым деп аталады.

6-Лекция. Математикалық сөйлем

Математикалық сөйлем – математикалық нысандар жөніндегі пайымды (немесе пікірді) өрнектейтін логикалық сөйлем.

Сөйлемнің субеъекті мен объекті, сәйкесінше математикалық сөйлемнің шарты (негізі, сілтемесі) және қорытындысы (салдары, нәтижесі) делінеді.

Математикалық сөйлемдерге: теорема, аксиома, постулат, анықтама, формулалар, теңдеулер мен теңсіздіктер, есептер т.б. жатады.

Ақиқаттығы дәлелдеусіз қабылданған математикалық сөйлем – аксиома деп атадады. Аксиома – гректің axioma – «бедел», «құрмет» деген сөзінен шыққан.

Аксиомалар жиыны мен алғашқы ұғымдар (нүкте, түзу, жазықтық, жиын) математикалық теорияның іргетасын құрайды. Ғылыми теориялардың бастамасы болатын аксиомалар жүйесіне олардың байланыссыздығы, қарама-қайшылықсыздығы, толықтығы сияқты талаптар қойылады.

Кез келген ұғымды немес ұғымдар арасындағы қатысты қанағаттандыратын талаптарды баяндайтын сөйлемдер постулаттар деп аталады. Постулат – латынның pospulatum – «талап», «ұсыныс» деген сөзінен шыққан.

Қисынды пайымдаулар арқылы дұрыс немесе бұрыстығы дәлелдеу нәтижесінде белгілі болатын пайым (сөйлем) теорема, деп аталады.

Математикалық сөйлемдер математикалық символдар арқылы да түсінікті өрнектеледі.

Мысалы,

Есеп. Параметрі бар теңдеулер жүйесін шешіңіз.

Шешуі: немесе

Жауабы:

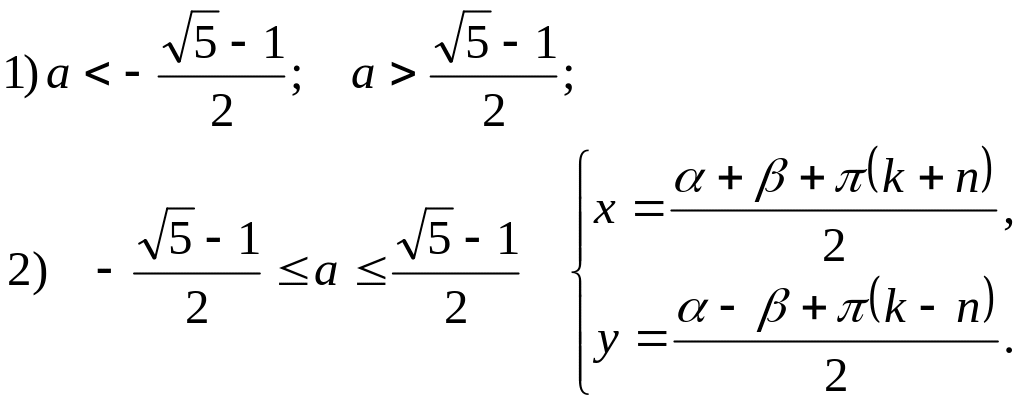
Көбінесе символдардың көмегімен жазылғанмен, математиканың символдарымен таныс оқушы, бұл сөйлемді еркін оқып, есептің шығарылуын оңай түсінеді.

Анықтамаға қойылатын маңызды талаптар:

1. Кез келген анықтама өлшемде болуы, яғни анықтаушы нысанның көлемі анықталған ұғымның көлемінен аспауы керек.

2. Анықталушы ұғымды сол ұғымның өзімен тікелей анықтауға болмайды.

3. Анықтамалар мүмкіндігіне қарай нысанды түрде кері анықталмауы керек.

Жаңа ұғымды ендіру барысында мұғалім оның белгілеріне назар аударуы керек. Егер мұғалім ұғымның анықтамасын тұжырымдап, кітаптағы берілген сызбаны көрсетумен шектелсе, онда оқушылар бұл ұғымды дұрыс меңгермейді.

Математикалық ұғымдарды саналы түрде меңгеруге мақсатты түрде қойылатын ауызша жаттығулар мен сұрақтар жүйесінің зор маңызы бар. Мысалы, қате анықтамалардан мысалдар келтіруге болады.

Сақтандыру жұмыстары:

• жаңа ұғымды формальді түрде ендірмеу керек;

• оқушыларды ұғымдар анықтамасын өзбетінше үйренуге баулу керек;

• ендірілген ұғымның, сөздің, анықтаманың тұжырымдамаларын табу (пайдалануға келтіру);

• әр сабаққа қажетті ұғымның анықтамасын қайталау;

• жаңа ұғым мен ескі ұғымның арасында байланысты орнату;

• анықтамаларды анық, дәл, қысқа, қатаң тұжырымдауды талап ету;

• 1-6 пункттер біртіндеп, сатылап орындалуы тиіс.

Қажетті және жеткілікті шарттарға мысалдар 1-кестеде келтірілген.

1-кесте – Қажетті және жеткілікті шарттардың орындалуына мысалдар

	Пікірлер
	Сөзбе-сөз тұжырымдау	Тұжырымдар	Басқаша тұжырымдау
1	Егер натурал сан жұп болса, онда ол 6-ға бөлінеді.		Натурал сан 6-ға бөлінуі үшін оның жұп болуы қажетті.
2	Егер натурал сан 6-ға бөлінсе, онда ол жұп		Натурал сан болуы үшін ол 6-ға бөлінуі жеткілікті.
3	Егер натурал сан жұп болса, онда ол 2-ге бөлінеді		Натурал сан 2-ге бөлінуі үшін ол санның жұп болуы қажетті және жеткілікті
4	Егер натурал сан 2-ге бөлінсе, онда жұп болғаны		Натурал сан жұп болуы үшін ол санның 2-ге бөлінуі қажетті және жеткілікті.

.

Қажетті, жеткілікті шарттарды анықтау

Анықтамалар.

1. Егер пікірі ақиқат болса, онда пікірі үшін қажетті шарт деп аталады.

2. Егер пікірі ақиқат болса, онда үшін пікірі жеткілікті шарт деп аталады.

3. Егер және импликациялары бір мезгілде ақиқат болса, онда шарты шартының қажетті және жеткілікті шарты деп аталады, яғни эквиваленттілік орындалады.

4. Ақиқаттығы тікелей дәлелдеу (талқылау) арқылы көз жеткізілетін математикалық сөйлем теорема деп аталады.

Теоремада мыналар анық көрсетілуі керек:

- белгілі бір нысандар (теореманың шарты) қандай шарттарда қарастырылады;

- бұл нысан туралы не тұжырымдалады (теореманың қорытындысы).

Теореманың шарты мен қорытындысын оңай анықтау үшін оны логикалық жалғауды қолдана отырып «егер, ..., онда...,» деген импликация түрінде жиі тұжырымдалады.

Мысалы, «параллелограмның диагоналдары қиылысады, және қиылысу нүктесінде қақ бөлінеді» деген теореманы былай тұжырымдауға болады:

Егер төртбұрыш параллелограм болса, онда оның диагоналдары қиылысады және қиылысу нүктесінде қақ бөлінеді.

Егер төртбұрыш параллелограмм болмаса, онда оның диагоналдары қиылысады және қиылысу нүктесінде қақ бөлінбейді.

Кері теорема: егер төртбұрыштың диагоналдары қиылысса және қиылысу нүктесінде қақ бөлінсе, онда бұл төртбұрыш – параллелограмм.

Егер төртбұрышта диагоналдары қиылысcа және қиылысу нүктесінде қақ бөлінбесе, онда бұл төртбұрыш – параллелограмм емес.

Конструктивті және рекурсивті анықтамалар

Нысанның қасиеттері, оны конструкциялау, нысанға жасалатын амал-дарды көрсету жолымен беріледі. Яғни, нысанның өзіндік ерекшеліктері амалдар түрінде беріледі.

Мысалы, формуласымен берілген функцияны сызықтық функция дейміз. Термин – сызықтық функция. Туыс ұғым – функция. Өзіндік ерекшелігі – – бірінші дәрежелі тәуелсіз айнымалы, мен – сандар және Яғни, егер сандармен айнымалылар арасында осындай амалдар берілген болса, онда сызықтық функция бар деп есептеледі. Егер амалдар (айнымалының дәрежесі) басқа болса, онда сызықтық функция болмайды.

Мысалы, арифметикалық прогрессияны анықтау. Екінші мүшесінен бастап өзінің алдындағы мүшеге тұрақты бір санды қосудан шығатын сан тізбегін арифметикалық прогрессия деп атаймыз. Туыстығы – тізбек. Термин – арифме-тикалық прогрессия, өзіндік ерекшелігі беріледі; ( – жалпы түрі), .

Егер алдындағы амалдардың белгілі бір және өзіндік ерекшеліктері көрсетілген болса, онда келесі мүшелерді алуға болады.

Теріс анықтама (қарама-қарсы анықтама). Қарама-қарсы анықтама нысанның қасиетін білдіре алмайды. Ол жіктеуші функцияның ролін атқарады. Егер нысандар класы топтарға бөлінсе, әрбір топтың белгілі бір қасиеттері болса, оған ат қойылса және өзіне тән емес қасиеттері көрсетілсе, онда бұл бір класқа жататын нысандарға қарама-қарсы анықтама беріледі.

Мысалы, бір жазықтықта жатпайтын және қиылыспайтын түзулерді айқас түзулер дейміз. Термин атауы – айқас түзулер, туыстығы – түзулер. Өзіндік ерекшелігі: 1) бір жазықтықта жатпайды; 2) қиылыспайды.

Сонымен, мектептегі анықтамалардың негізгі типологиясы – нысандардың өзіндік ерекшеліктерін көрсететін амалдардың ерекшелігін түсіну.

Математикалық нысанды анықтауға мысалдар 2-кестеде көрсетілген.

2-кесте – Математикалық нысанды анықтау

Сипаттамалық қасиетін жазу жолмен берілген анықтама	Консруктивті анықтама	Қарама-қарсы анықтамалар	Айқындалмаған анықтамалар
теңдеу (V сынып.) 2) ромб (VII сынып.)	О нүктесінде симметриялы фигуралар (VI сынып.)	Пропорционал сандар (VII сынып.)	Нүкте және түзу (VII сынып)

Тапсырмалар

1. Анықтамаларға логикалық талдаулар жасаңыздар, яғни ұғымның туыстық аты және өзіндік ерекшеліктерін атаңыздар. Таңдап алынған әрбір анықтаманың өзіне тән әртүрлі ерекшеліктерін сипаттаңыздар.

2. Келесі анықтама анықтамаға қойылатын талаптарды орындай алатындығын немесе орындай алмайтындығын анықтаңыздар:

1. «Үшбұрыштың төбесі мен оған қарама-қарсы жатқан қабырғасының ортасын қосатын кесінді үшбұрыштың медианасы деп аталады».

2. «Бірлік шеңбердің нүктесін радианға бұрудан шыққан нүктесінің ординатасын бұрыштың синусы деп атайды».

3. «Бір-бірінен өзгешелігі тек таңбасында болатын екі санды қарама-қарсы сандар деп атайды».

Өзіндік ерекшеліктері конъюнктивті (барлық қасиеттері бір мезгілде біреуінен табылатын) болатын және болмайтын нысандарға мысал 3, 4-кестелерде келтірілген.

3-кесте – Өзіндік ерекшеліктері конъюнктивті болатын нысандарға мысал

№	Мысалдар	Үшбұрыш (иә «+», жоқ «–»)	Екі қабырғалары бір-бірімен тең +, –	Қорытынды: берілген нысан тең бүйірлі үшбұрыш.
1 2 3 4	2 ,5	– + + +	– – + +	– – + +

4-кесте – «Алымы бөлімінен артық немесе тең болатын бөлшекті бұрыс бөлшек дейміз» – анықтамасына мысалдар

Нысандар		Бөлшек	Алымы бөлімінен көп		Бұрыс бөлшек
1 2 4	100	+ – + +	– – + –	– – – +	– – + +

Өзіндік ерекшеліктері дизъюнктивті түрде біріктірілген, туыстық қасиет-тері сақталған, ең кем дегенде бір өзгешелігі айтылған.

Тапсырмалар.

Келесі анықтамалардың эквивалентті (мәндес) екенін анықтаңыздар:

1. а) -қа тең бұрыш тік бұрыш деп аталады.

б) жазық бұрыштың жартысын тік бұрыш дейміз.

2. а) Белгісіз саны әріппен белгіленген теңдік теңдеу деп аталады.

б) Айнымалыдан тұратын теңдік теңдеу деп аталады.

7-Лекция. Теоремаларды дәлелдеуге үйрету

Теорема ұғымын қатаң түрде анықтау тек формальды теорияларда кездеседі. Мектеп математика курсы сияқты формальді емес теорияларда теорема ұғымына тек түсініктеме беріледі: қисынды пайымдаулар арқылы дұрыс немесе бұрыстығы дәлелдеу нәтижесінде белгілі болатын пайым (сөйлем) теорема, деп аталады. Теорема – грек сөзі, ол: «көз жеткіземін», «ойлап көремін» деген мағыналарды білдіреді.

Теореманың түрлері: келісімді теорема (мысалы: «Вертикаль бұрыштар тең»); шартты теорема («егер ..., онда...»).

Теореманың бөліктері: 1) теореманың шарты, 2) теореманың қорытындысы, 3) теореманың түсінік беру бөлігі.

Бұрын дәлелденген теоремалардан тікелей шығатын кейбір теоремаларды

салдарлар, деп атайды.

Салыстырмалы түрде, дәлелдемесі қысқа, өз алдына дербес мәнге ие болмайтын және басқа теоремаларды дәлелдеу үшін пайдаланытатын теоремаларды лемма, деп атайды. Лемма – грек сөзі, «табыс» деген мағынада [18].