Джанабердиева С.А.

Есептер шешудің әдістемелік негіздері

Дәрістер тезистері

1. Лекция. Есептердің түрлері, шығару әдістері және есте ұстайтын қағидалар. Оқылатын бағдарламаға сәйкес есептер стандарт және стандарт емес есептер, берілуі мен шығарылу тәсіліне қарай графиктік, геометриялық, кестелік, салу, есептеу, дәлелдеу, логикалық, қызықты, ойын есептер, «қақпан» есептер, математикалық викториналар, софизмдер, сөзтізбектер мен қиылысулар, мәселе есептер, ашық және жабық тестер т.б.; мазмұнына қарай пайыздарға, қозғалысқа, қоспаларға, пропорцияға т.б. берілген есептер, статистикалық, дифференциалдық есептер, элементар математикаға, жоғары математикаға берілген есептер, орындалу функциясына қарай белгісіз шаманы табу, теңдеуді, теңсіздікті шешу, функцияның анықталу аймағын, функцияның мәндерінің аймағын табу; күрделілігіне қарай қарапайым, орта, жоғары деңгейлік есептер, конкурстық (олимпиадалық, жарыс) жас ерекшеліктерге байланысты 1-сыныпқа арналған, 2-сыныпқа арналған т.с.с. болып бөлінеді.

І. Есептерді шығару және дәлелдеу әдістері.

Есептерді шығару мен дәлелдеуде келесі әдістер пайдаланылады: есептеуді пайдалану, координаталық жүйені пайдалану, математикалық индукцияны қағидасын пайдалану, теріс жору, аддитивтік әдіс, дедукцияны пайдалану, салудың әдістері, стандарт әдіс, стандарт емес әдістер, логикалық ойлау т.б.

ІV. Математикалық есептерді шығаруда есте ұстайтын қағидалар: жиілік, параллельдік, озық жоғары қиындындықтылық, идеяның тиімділігі, жауаптың тиімділігі, вариативтілік, өзін-өзі бақылау, тез қайталау, текстпен жұмыс істеу, жағдайды модельдеу қағидалары т.б.V. Конкурстық есептер. Олимпиадалық, жарыс, ойын, математикалық викториналар т.б.

2. Лекция. Ньютон биномы, куб теңдеулер үшін Виет теоремасы, санның бөліктері. Безу теоремасы. Горнер кестесі.

Лекцияның мақсаты: Ньютон биномы, Дәрежелі номдар. Қысқаша көбейту формулалары. Паскаль үшбұрышы. Безу теоремасы. Горнер кестесі. куб теңдеулер үшін Виет теоремасын пайдаланып есептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту.

I. Ньютон биномы, Дәрежелі номдар. Қысқаша көбейту формулалары

Ньютон биномы:

Мұндағы дегеніміз нен тәуелді қандай да бір оң сан.

1-мысал. Кез келген натурал ( ) үшін санының ға қалдықсыз бөлінетінін дәлелдеңіз.

Шешуі: формуласын пайдалансақ:

саны ға қалдықсыз бөлінеді. Д.к.о.

II. Паскаль үшбұрышы. Безу теоремасы. Горнер кестесі

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1 Т.с.с.

Паскаль үшбұрышын Ньютон биномының коэффициенттерін табуға қолдануға мысал келтірейік.

2-мысал.

қайталанатын: терулер мен орналастырулар:

Безу теоремасы. Горнер кестесі. Безу ((1730-1783) француз математигі) теоремасы. – дегі қалдық .

Ал, Горнер схемасы бойынша: .

Мысалы: 1)

;

2)

	3	0	-2	0		1
		1
	3	1

3)

	1		2		-3		0		1				-4
					2		-1		-1				0
	-2		2		-1		-1		0
					-4		10		-18
	-1		2		-5		9
					-2		7
			2		-7

2	1 3 -17 2 10	14 -14
	1 5 -7

Егер болса, көпмүше сызықтық екімүшеге қалдықсыз бөлінеді.

Мысалы. көпмүшесі сызықтық екімүшесіне қалдықсыз бөлінеді, себебі: ; ендеше берілген көпмүшенің түбірі болады. Яғни және

Безу теоремасы көпмүшелердің бөлінгіштігі жайындағы теоремадан шығатын салдарлардың бірі болып табылады.

Безу теоремасы. көпмүшесін екімүшесіне бөлгендегі қалдық -тің -дағы мәніне, яғни -ға тең болады: , мұндағы – толымсыз бөлінді.

Көпмүшелердің бөлінгіштігі жайындағы теоремадан шығатын екінші салдар. Егер саны көпмүшесінің түбірі болса, онда көпмүшесі екімүшесіне қалдықсыз бөлінеді (яғни, қалдық нольге тең болады).

Көпмүшелердің бөлінгіштігі жайындағы теоремадан шығатын үшінші салдар. Бүтін коэффициентті көпмүшесінің әрбір бүтін түбірі (егер бар болса) оның бос мүшесінің бөлгіштері болып табылады.

Мысал. көпмүшесінің бос мүшесі 2-нің бөлгіштері , болып табылады.. Тексеру арқылы екенін көреміз, ендеше: осыдан: ; өрнегін көбейткіштерге жіктеу үшін 30-дың бөлгіштерінің ( ) ішінде екенін байқау қиын емес, осыдан: көбейткіштеріне жіктейміз.

III. Куб теңдеулер үшін Виет теоремасы

3. Лекция. Комплекс сандарға амалдар қолдану.

Комплекс санның тригонометриялық формасы

Комплекс санның аргумент (бұрышы): . a – абцисса, b – ордината;

4. Лекция. Стандарт емес есептер. Коши теңсіздігі

Лекцияның мақсаты: Стандарт емес есептерді шығару әдістерін оқып үйрену. Білім, білік, дағды, шығармашылық ойлауды дамыту.

І. Стандарт емес есептердің анықтамасы.

Жалпы орта білім беретін мектеп математикасының курсына енбейтін материалдар бойынша құрылған есептер стандарт емес есептер деп аталады.

Көбінесе мұндай есептер Коши теңсіздігін, Бернулли теңсіздігін, Коши-Буняковский теңсіздігін, күрделі есептерге Ньютон биномын қолдану, куб теңдеулер үшін Виет теоремасын, санның бөліктерін, комплекс сандарға амалдар қолдануды, математикалық индукция әдісін, санның бүтін және бөлшек бөліктерін, комбинаторика элементтерін, математикалық орталарды салыстыруды, логиканы т.б. жаңа әдістерді пайдалану арқылы шығарылады.

ІІ. Стандарт емес есептерге мысалдар

1-мысал. Коэффициенттердің қосындысын табыңыз .

Шешуі: болғанда көпмүшесінің мәні коэффициенттерінің қосындысына тең екенін ескерсек: . Жауабы: 0.

2-мысал. сандарының арифметикалық, геометриялық, (пропорционалдық), гармониялық, квадраттық, куб дәрежелік орталарын тауып салыстырыңыз.

; ;

I. Кошидің теңсіздігін есептер шығаруға пайдалану

II. Коши теңсіздігін пайдалануға берілген стандарт емес есептерге мысалдар қарастыру.

3-мысал. Коши теңсіздігін дәлелдеңіз.

Дәлелдеуі: ; ; ; ; . Егер болса, онда ; , мұндағы ; ал егер болса, онда

4-мысал. Теңдеуді шешіңіз .

Шешуі: Теңдеудің сол жағындағы әрбір қосылғышқа жеке-жеке Коши теңсіздігін қолданайық:

Теңдеулерді мүшелеп қоссақ:

түбірлері: анықталу облысын қанағаттандырмайды. Ендеше, шешімі жоқ. Жауабы: шешімі жоқ.

2-мысал. Теңдеуді шешіңіз

Шешуі: Коши теңсіздігі бойынша: екенін ескерсек, берілген теңсіздікті түрлендіре аламыз: . Осыдан ; . Жауабы: 0.

5. Лекция. Бернулли теңсіздігі. Коши-Буняковский теңсіздігі. Санның бөліктері

Бернулли теңсіздігін стантарт емес есептер шығаруға пайдалану

Лекцияның мақсаты: Стандарт емес есептерді шешуде жиі пайдаланылатын Бернулли, Коши-Буняковский теңсіздіктерін стандарт емес есептер шығаруға пайдалану. Білім, білік, дағды, шығармашылық ойлауды дамыту.

Бернуллидің үшін теңсіздігін есептер шығаруға пайдалану. Бернулли теңсіздігін пайдалануға берілген стандарт емес есептерге мысалдар

1.мысал. Бернуллидің үшін теңсіздігін математикалық индукция әдісін пайдаланып дәлелдейік.

1. үшін теңсіздік тура;

2. үшін теңсіздік тура делік;

3. үшін теңсіздіктің тура екенін дәлелдейік:

, ұйғарымы бойынша: ; бірақ ; ендеше: теңсіздігі күшейеді де үшін дұрыстығынан берілген теңсіздіктің дұрыстығы кез келген үшін дәлелденеді. Д.к.о.

2-мысал. Теңдеуді шшіңіз .

Шешуі: Теңдеудің сол жағындағы әрбір қосылғышқа Бернулли теңсіздігін қолдансақ: . Теңдеудің таңбасы тек болғанда дұрыс, яғни . Жауабы: .

Жуық есептеулер үшін: ; .

4-мысал. .

5-мысал. .

6-мысал. .

7-мысал. .

Коши-Буняковскийдің - оң константасы үшін болғанда орындалатыны жөніндегі теңсіздігін есептер шығаруға пайдалану

Санның бөліктеріне есептер шығару

Санның өзінен аспайтын ең үлкен бүтін санды санның бүтін бөлігі деп атайды.

. Мысалы: .

Сан мен оның бүтін бөлігінің айырмасын санның бөлшек бөлігі деп атайды.

. Мысалы:

6. Лекция. Алгебралық, транцендент өрнектер, теңдеулер мен теңсіздіктер, олардың жүйелері мен жиынтықтары. Қарапайым теңдеулер дифференциал

Алгебралық теңдеулердің жүйелері мен жиынтықтары.

Лекцияның мақсаты: теңдеулер жүйесін шешуді, жаңа белгісіздер енгізуді, симметриялық теңдеулердің жүйелері мен жиынтықтарын, симметриялық теңдеулер жүйесін, алгебралық функцияларды, олардың графиктерін есептер шығаруға қолдана білу. Білім, білік, дағды, шығармашылық ойлауды дамыту.

I. Теңделерді, теңдеулер жүйесін шешу. Жаңа белгісіздер енгізу

II. Алгебралық, модуль таңбасы бар теңдеулердің жүйелері мен жиынтықтарына берілген есептерді шығару жолдарын қайталау.

III. Симметриялық теңдеулер жүйесін шешуәдістерін қайталау..

ІІІ. Алгебралық функциялар. Олардың графиктерін қайталау.

ІV. Виет теоремалары. Кардано формулалары. Ферма теоремалары.

Математикада көп жаңалықтардың ашылуына себепші болған, бірақ математикада маңызды роль атқармайтын, 1995 жылға дейін дәлелденбегендіктен, ешбір математикалық оқулықтар мен анықтамаларға енбеген «Ферманың» Үлкен теоремасы: натурал көрсеткішті келесі теңдеудің бүтін сандар жиынында шешімі болмайды: . Теореманы дәлелдемегендіктен оның атымен аталуы дәстүрлік түрде болған.

Орта мәндер жөніндегі Ферма теоремасы: интервалында анықталған функция осы интервалға тиісті нүктесінде өзінің ең үлкен немесе ең кіші мәніне жететін болса, онда функцияның осы нүктедегі бірінші туындысы . Математикалық талдауда Ферманың басқа да теоремалары қолданылады.

Алгебралық теңдіктердің жүйелері мен жиынтықтарын, алгебралық теңсіздіктер жүйесін шешуді, жаңа белгісіздер енгізуді, симметриялық теңдеулер жүйелері мен жиынтықтарын есептер шығаруға қолдана білу. Білім, білік, дағды, шығармашылық ойлауды дамыту.

Симметриялық жүйелерді шешуде пайдаланылатын көмекші белгісіз енгізу әдістері:

Т.б.

ІV. Қарапайым дифференциал теңдеулерді шешу

. Мысалы, парашютистің парашюті ашылмаған жағдайда жылдамдық шамамен 50 м/с, ал парашют ашалған жағдайда жерге жақын жылдамдық шамамен 4-5 м/с.

7. Лекция. Трансцендент өрнектер теңдеулер мен теңсіздіктер олардың жүйелері мен жиынтықтары, функциялары

Транцендент теңдеулердің жүйелері мен жиынтықтары.

Лекцияның мақсаты: жаңа белгісіздер енгізуді, симметриялық, трансцендент модуль таңбасы бар теңдеулер жүйелері мен жиынтықтарын, симметриялық теңдеулер жүйесін, трансцендент функцияларды, олардың графиктерін есептер шығаруға қолдана білу. Білім, білік, дағды, шығармашылық ойлауды дамыту.

I. Трансцендент теңдеулер жүйесін шешу. Жаңа белгісіздер енгізу.

II. Транцендент, әрі модуль таңбасы бар теңдеулердің жүйелері мен жиынтықтарына берілген есептер

III. Симметриялық теңдеулер жүйесін шешу.

IV. Трансцендент функциялар. Олардың графиктері. Қайталау

8. Лекция. Абсолют таңбасы, параметрі бар теңдеулер, теңсіздіктер және олардың жүйелері мен жиынтықтары.

Абсолют таңбасы бар теңдеулер олардың жүйелері мен жиынтықтары.

Лекцияның мақсаты: абсолют таңбасы бар теңдеулерге және олардың жүйелері мен жиынтықтарына берілген сесептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту.

I. Абсолют таңбасы бар теңдеулер олардың жүйелері мен жиынтықтары.

II. Абсолют таңбасы бар теңсіздіктер және олардың жүйелері мен жиынтықтары

Параметрі бар теңдеулер және олардың жүйелері мен жиынтықтары.

Мақсаты: параметрі бар теңсіздіктер және олардың жүйелері мен жиынтықтарына берілген сесептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту. Өткен пәндерден қайталау.

9. Лекция. Шектер.

Лекцияның мақсаты: Шектерге есептер шығару, 1-2-тамаша шектерді, анықталмағандықтарды анықтау ережелерін пайдаланатын есептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту. Өткен пәндерді қайталау.

I. Шектерге есептер шығару

II. 1-2 тамаша шектер, Лапитал т.б. ережелерді қайталау.

III. Анықталмағандықтарды анықтау ережелерін пайдаланатын есептер шығару

10. Лекция. Координаттар әдісі. Вектор

Координаттар әдісі. Вектор

Лекцияның мақсаты: Координаттар, математикалық индукция қағидасын қолданатын т.б. әдістерді пайдаланып есептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту. Өткен пәндерден қайталау.

І.Координаттар әдісін қолданып есептер шығару

II. Математикалық индукция қағидасын пайдаланып дәлелдеуді қайталау.

11. Лекция. Мәселе есептерді шешудің моделін жасау

Мәселе есептерді шешудің моделін жасау. Өткен пәндерден қайталау.

Лекцияның мақсаты: Мәселе есептерді шешудің моделін жасау. Білім, білік, дағды, шығармашылық ойлауды дамыту.

I. Мәселе есептерді шешудің моделін жасау

II. Әр типтегі мәселе есептерін шығару

1. Массасы тұрақты болатын түзу сызықты бірқалыпты қозғалатын денеге әсер етуші күш бойынша оның қозғалыс формуласын анықтау есебін дифференциалдық теңдеулер құру арқылы шығарылу жолы жоғарыда келтірілген. Сол сияқты келесі есептердің де шешулері жоғарыда келтірілген (қарапайым дифференциалдық теңдеулер құру):

2.Ауырлық күшінің көмегімен вертикаль қозғалыстың координатасы мен массасы бойынша дифференциалдық теңдеу құру және оны шешу;

3.Физика мен техника есептерінің көбін шығаруға болатын дифференциалдық теңдеу;

4.Радиактивтік ыдырау есебі;

5.Гармониялық тербелістердің дифференциалдық теңдеуін пайдалану;

6. Гук, Ньютон заңдары бойынша дифференциалдық теңдеулер құру

7. Атмосфералық ортада денелердің құлауы жөніндегі күрделірек есеп;

III. Пойяның есепті қалай шығару керек деген еңбегі бойынша дискуссия ұйымдастыру

12. Лекция. Ықтималдар теориясының элементтері

Лекцияның мақсаты: Комбинаториканы, ықтималдар теориясын пайдаланып шығарылатын есептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту. Өткен курстардан қайталау

I. Ықтималдар теориясын пайдаланып шығарылатын есептер шығару

II. Қайталанылмайтын орналастырулар, алмастырулар, терулерді пайдаланып шығарылатын есептер шығару

IІІ. Қайталанылатын орналастырулар, алмастырулар, терулерді пайдаланып шығарылатын есептер шығару

13. Лекция. Математикалық статистика есептері

Лекцияның мақсаты: Математикалық статистика есептерін, орталарды есептеуді, мода, құлаш, дисперсияны пайдаланып есептер шығару. Кіші-гірім социологиялық статистика жүргізіп, оған математикалық талдау жасау. Білім, білік, дағды, шығармашылық ойлауды дамыту. Қайталау.

I. Математикалық статистика есептерін, орталарды есептеуді пайдаланып есептер шығару

II. Мода, құлаш, дисперсияны пайдаланып есептер шығару

ІІІ. Кіші-гірім социологиялық статистика жүргізіп, оған математикалық талдау жасау.

14. Лекция. Планиметрия мен стереометрия есептері. Симпсонның универсал формуласы. Осы тақырып бойынша материалдарды қайталау.

Кеңістіктегі салу есептері т.б.

Лекцияның мақсаты: Кеңістіктегі салу есептерін, т.б. Білім, білік, дағды, шығармашылық ойлауды дамыту.

Дұрыс көпжақтардың модельдерін жасау

Дұрыс көпжақтардың моделін жасау оқушыларды қатты қызықтырады. Сыныптан тыс жұмыстарда білім алушыларға стереометриялық фигуралардың моделін жасау тапсырылады. Бұл олардың жазықтықтағы және кеңістіктегі танымдылығын дамытады.

Анықтама. Егер дөңес көпжақтың барлық жақтары дұрыс көпбұрыштар болса, сонымен қатар оның әрбір төбесінде саны бірдей қырлар тоғысса, ондай дөңес көпжақ дұрыс көпжақ деп аталады,

Дөңес дұрыс көпжақтардың бес түрі болады: куб (алты шаршыдан құралған), дұрыс тетраэдр (төрт дұрыс үшбұрыштан құралған), дұрыс октаэдр (сегіз дұрыс үшбұрыштан құралған дұрыс сегізжақ), додекаэдр (он екі дұрыс бесбұрыштардан құралған дұрыс он екі жақ), икосаэдр (жиырма теңқабырғалы үшбұрыштан құралған дұрыс жиырма жақ).

1-5-суреттерде аталған көпжақтардың моделін жасау үлгілері көрсетілген. Жазбаларды масштаб бойынша үлкейтіп, тігіс үшін шетінен жолақ қалдырып қиып, содан соң желімдеу керек. Модельдердің өлшемін үлкен етіп жасаған әдемі көрінеді.

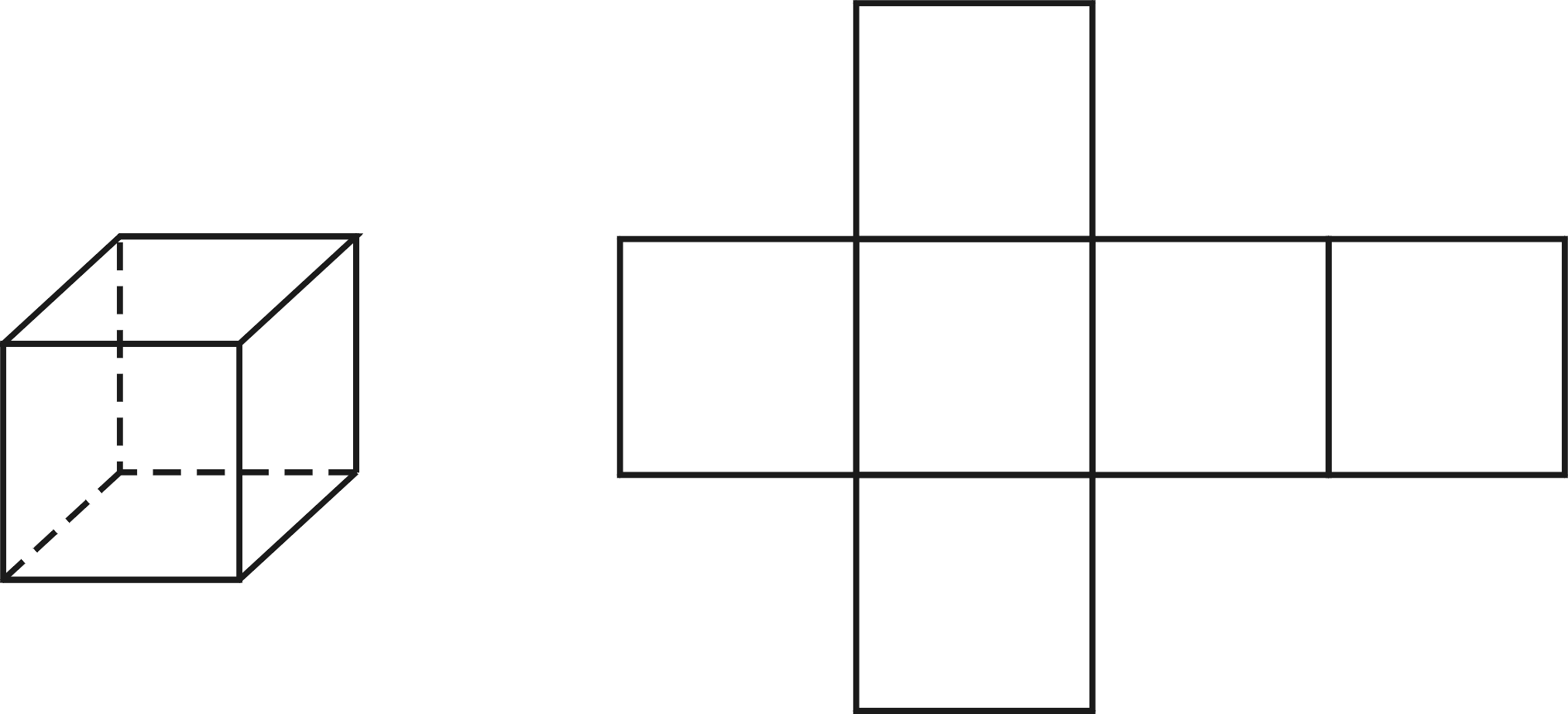
1-сурет. Куб және оның жазбасы 2-сурет. Дұрыс тетраэдр және

оның жазбасы

3-сурет. Октаэдр және оның жазбасы

4-сурет. Додекаэдр және оның жазбасы

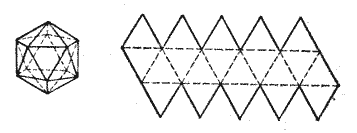
5-сурет. Икосаэдр және оның жазбасы

Енді, осы көпжақтардың формулаларын көрсетейік. Ол үшін келесі белгілеулерді енгіземіз: V – көпжақтың көлемі, S – көпжақ бетінің ауданы, R – көпжаққа сырттай сызылған сфераның радиусы, r – көпжаққа іштей сызылған сфераның радиусы, h – қөпжақтың биіктігі (мағынасы болса), a – көпжақтың бір-біріне тең болатын әрбір қыры.

Куб (дұрыс гектаэдр): .

Тетраэдр: .

Октаэдр: .

Додекаэдр:

.

Икосаэдр:

Дұрыс көпжақтардың қабырғаларының, төбелерінің және жақтарының саны Эйлер формуласы бойынша өзара байланыста болады: . Мұндағы – төбелер саны, – қабырғалар саны, – жақтар саны.

Енді, көпжақтардың классификациясы: Платон денелері – дөңес дұрыс көпжақтар, Пуансо денелері – дөңес емес, Архимед денелері – дөңес жартылай дұрыс көпжақтар, Архимед призмасы мен антипризма – көпжақтар және Федоров денелері – дөңес параллелоэдрлер

Симпсонның әмбебап (универсал) формуласы

Бізді қоршаған айналамызда кездесетін ағаштардың бұтақтары, діңдері мен жапырақтары пішіні жағынан, әрине, біз білетін көпжақтарға да, цилиндр, конус, қиық конус сияқты айналу денелеріне де келмейді. Осындай формадағы денелердің өлшемдерін жуықтап табу үшін есте сақтауға да, пайдалануға да ыңғайлы ортақ формула бар ма? Иә, математикада ондай әмбебап формула бар және ол Симпсон формуласы деп аталады:

,

мұндағы h – дененің биіктігі; – төменгі табан ауданы; – дене биіктігінің ортасындағы көлденең қимасының ауданы; – жоғарғы табан ауданы.

Қарастырып отырған дененің пішіні біз білетін қандай да бір фигураға ұқсайтын болса, онда осы бір ғана формуланың көмегімен оның көлемін және жазық фигуралардың ауданын жуықтап табуға болады.

Төмедегі фигуралардың көлемін осы формула арқылы шығарып алуға болады.

Призма мен цилиндр үшін

.

Пирамида мен конус үшін

.

Қиық конус үшін

Қиық пирамида үшін де осыған ұқсас дәлелденеді;

Шар үшін

.

Енді әмбебап формуланы жазық фигуралардың ауданын табуға қолдануды қарастырайық.

Ауданды есептеу формуласының жалпы түрі: ,

мұндағы h – фигураның биіктігі, – төменгі табан ұзындығы, – орта сызық ұзындығы, – жоғарғы табан ұзындығы.

Параллелограмм (шаршы, тіктөртбұрыш) үшін: .

Трапеция үшін: .

Үшбұрыш үшін: .

Үш перпендикуляр жазықтық. Қаңбақ

Қатты қағаздан радиустары бірдей үш дөңгелек қиып алыңыз. Диаметрлерін жүргізіңіз. Дөңгелектердің диаметрлерін 7-суретте көрсетілген кесінділердің бойымен қиыңыз. Дайын болған үш дөңгелекті бір-бірімен қиылыстырыңыз. Жасалған фигура «Қаңбақ» деп аталады (8-суретте).

Бұл кеңістіктегі үш өлшемді декарттық координаталар жүйесінде берілген есептерді шешу үшін көрнекі құрал болып табылады.

Берілген дөңгелектерді қиылыстырып орналастыру үшін қажетті кесінділер көрсетілмесе, бұл – күрделілігі жоғары бас қатыру есебі болып табылады.

7-сурет

Дайын модель 8-суретте көрсетілген.

Планиметрияның тамаша теоремалары

Лекцияның мақсаты: Планиметрияның тамаша теоремаларын пайдалануға берілген т.б. стандарт емес есептер шығару. Білім, білік, дағды, шығармашылық ойлауды дамыту.

I. Чева, Менелай теоремалары

II. Птолемей, Дезарг, Брианшан, Стюарт, Паскаль, Гаус теоремалары

III. Эйлер, Симпсон түзулері,

IV.Эйлер шеңбері

8-сурет

V.Гильберт, Пьеано аксиомалары

Теоремалар:

«егер алтыбұрыш сырттай сызылған болса, онда... (оның қарама-қарсы төбелерін қосатын кесінділер бір нүктеде қиылысады)»;

Паскаль теоремасы. «Егер іштей сызылған алтыбұрыштың қарама-қарсы қабырғалары параллель болмаса, онда... (осы қабырғалардың созындыларының қиылысу нүктелері бір түзуге тиісті болады)»;

Пталомей теоремасы. «Егер төртбұрыш іштей сызылған болса, онда... (оның диагональдарының көбейтіндісі оның қарама-қарсы қабырғаларының ұзындықтарының көбейтінділерінің қосындысына тең)»;

«егер дөңес көпбұрыш дұрыс болса, онда... (оған іштей және сырттай шеңбер сызуға болады. Бұл шеңберлердің центрлері беттеседі)»;

«егер үшбұрыш іштей сызылған болса, онда... (оған сырттай сызылған шеңбердің центрі, ортоцентр және үшбұрыштың ауырлық центрі Эйлер түзуі деп аталатын бір түзүдің бойында жатады)»;

Дезарг теоремасы. «Егер және үшбұрыштарының сәйкес төбелерін қосатын түзулер бір нүктеде қиылысса, онда... (олардың сәйкес қабырғалары арқылы жүргізілген түзулердің қиылысу нүктелері бір түзуге тиісті)»;

Пифагор теоремасы. «Егер үшбұрыш тікбұрышты болса, онда... (оның гипотенузасының квадраты катеттерінің квадраттарының қосындысына тең)» немесе «Егер үшбұрыш тікбұрышты болса онда... (оның гипотенузасына салынған шаршының ауданы катеттерге салынған шаршылардың аудандарының қосындысына тең)»;

Пифагор теоремасына кері теорема. «Егер үшбұрыштың бір қабырғасының квадраты қалған екі қабырғаларының квадраттарының қосындысына тең болса,

онда... (үшбұрыш тікбұрышты болады)».

Математикалық сөйлемдер жарысы (Екі ойыншы немесе топ жетекшілерінің жарысы).

1,а. Үшбұрыштың бұрыштарының қосындысы 180 -қа тең.

2,а. Үшбұрыштың сыртқы бұрышы онымен сыбайлас емес екі ішкі бұрыштың қосындысына тең.

3,ә. Егер екі параллель түзу үшінші түзумен қиылысса, онда ішкі айқыш бұрыштар тең болады.

4,ә. Егер екі параллель түзу үшінші түзумен қиылысса, онда ішкі тұстас бұрыштардың қосындысы 180 -қа тең болады.

5,б. Үшбұрыштың медианалары ауырлық центрінде қиылысады.

6,б. Үшбұрыштың биіктіктері ортоцентрде қиылысады

7,в. Үшбұрыштың биссектрисалары іштей сызылған шеңбердің центрінде қиылысады.

8,в. Үшбұрыштың орта перпендикулярлары сырттай сызылған шеңбердің центрінде қиылысады.

9,г. Үшбұрыштың биссектрисасы осы бұрышқа қарсы жатқан қабырғасын оған іргелес жатқан қабырғаларына пропорционал бөліктерге бөледі.

10,г. Үшбұрыштың медианаларының қиылысу нүктесі медиананы үшбұрыштың төбесінен бастап 2:1 бөліктерге бөледі.

11,ғ. Үшбұрыштың ауданы табаны мен биіктігінің көбейтіндісінің жартысына тең.

12,ғ. Ромбының ауданы диагональдарының көбейтіндісінің жартысына тең.

13,д. Үшбұрыштың ауданы екі қабырғасы мен олардың арасындағы бұрыштың синусының көбейтіндісінің жартысына тең.

14,д. Герон формуласы: Үшбұрыштың ауданы түбір ішіндегі жарты перимерт және жарты перимерт мен қабырғаларының жеке-жеке айырымдарының көбейтіндісіне тең.

15,е. Тікбұрышты үшбұрыштың гипотенузасының ортасы оған сырттай сызылған шеңбердің центрі болады.

16,е. Тікбұрышты үшбұрыштың гипотенузасы ұзындығының жартысы оған сырттай сызылған шеңбердің радиусына тең.

17,ж. Үшбұрышқа сырттай сызылған шеңбердің радиусы оның қабырғаларының көбейтіндісін оның төрт еселенген ауданына бөлгенге тең.

18,ж. Үшбұрышқа іштей сызылған шеңбердің радиусы осы үшбұрыштың екі еселенген ауданын оның периметріне бөлгенге тең.

19,з. Тік бұрышты үшбұрыштың тік бұрышынан гипотенузасына түсірілген биіктігі катеттердің гипотенузадағы проекцияларының геометриялық ортасына тең.

20,з. Үшбұрыштың қабырғалары қарсы жатқан бұрыштарының синустарына пропорционал болады. Т.с.с.

5-бөлім. Әрі қарай жалғастырыңыз. Топ мүшелерінің жарысы.

1,а. (Эйлер шеңбері немесе тоғыз нүкте шеңбері). «Центрі үшбұрышқа сырттай сызылған шеңбердің центрі мен үшбұрыштың ортоцентрін қосатын кесіндінің ортасында болатын, ал радиусы сырттай сызылған шеңбер радиусының жартысына тең шеңбер келесі тоғыз нүкте арқылы өтеді: 1)... (үшбұрыштың биіктіктерінің табандары), 2)... (үшбұрыштың қабырғаларының орталары), 3. ... (үшбұрыштың төбелері мен ортоцентрді қосатын кесінділердің орталары)».

2,а. Гаусс теоремасы. «Төртбұрыштың қарама-қарсы қабырғаларының созындыларының қиылысу нүктелерін қосатын кесіндінің ортасы... (оның диагональдарының орталары арқылы өтетін түзуге тиісті).

3,ә. Стюарт теоремасы. « үшбұрышының төбесінен жүргізілген биссектрисасының қабырғасымен киылысу нүктесі болсын. Сонда... (келесі теңдік тура: )».

4,ә. Брианшон теоремасы. «Сырттай сызылған алтыбұрыштың қарама қарсы төбелерін қосатын кесінділер… (бір нүктеде қиылысады)».

Планиметрия және стереометрия есептері

Планиметрия және стереометрия есептерін, жазықтықтағы және кеңістіктегі салу есептерін шығару.

жазықтығынан түзуін және көпжақтың бір жағының жазықтығын таңдап алып, олардың қиылысуынан нүктесін саламыз. жазықтығын онда жазықтығының берілген бір нүктесі жататындай түрде таңдап аламыз. жазықтықтарында жататын екі нүкте алып, және жазықтықтарының қиылысу сызығын саламыз. нүктесін салу үшін түзуі арқылы өтетін қосымша жазықтығын жүргіземіз және болатындай қиылысу сызығы мен нүктесін саламыз, онда .

Егер көпжақ призма болса, онда жазықтығы әдетте бүйір қабырғасына жүргізіледі, ал егер көпжақ пирамида болса, жазықтығы пирамиданың төбесі арқылы өтеді. Келесі 3-есептің және диссертацияда келтірілген осы сияқты басқа есептердің шешулері осы тәсіл арқылы көрсетіледі.

1-есеп. Призманың қима жазықтығын салу керек, мұндағы , егер

Шешуі. І жағдай. деп белгілейік. түзуі ретінде түзуін таңдап таңдап аламыз, жазықтығы ретінде жазықтығын аламыз, жазықтығының ролін атқарады. Салу:

1) 2)

3) 4)

5) ; 6. – ізделген қима.

ІІ жағдай. мен түзулері қиылыспайды, немесе олардың қиылысу нүктесі сызбадан тыс болады. кесіндісінен нүктесін таңдап аламыз және болатындай нүктесін саламыз. Бұдан соң түзуін жүргіземіз, сондай-ақ болатындай нүктесін табамыз. – ізделінді қима. Егер , онда . Егер нүктесін кесіндісінен таңдап алынса және ол нүкте – диагональдық қимада жатса, онда: және салу жұмысы ықшамдалады.

Призманың немесе пирамиданың қимасы бір түзудің бойында жатпайтын үш нүкте арқылы бір мәнді анықталады, онда қима салу есебінің бір ғана шешуі болады, сондықтан есепке зерттеу жүргізудің қажеті болмайды. Қима салу есебінің сәтті болуы ең алдымен түзу мен жазықтықтың қиылысу нүктесін сала білуге тікелей байланысты.

2-есеп. Тікбұрышты параллелепипедттің диагоналы табанымен бұрыш, ал бүйір жағының диагоналы табан жазықтығымен бұрыш жасайды. Аталған диагоналдар арасындағы бұрышты табыңыздар.

Шешуі. тікбұрышты параллелепипед берілсін. және болсын. бұрышын табайық (9-сурет).

9-сурет

Екі жақты бұрыш болатын үшжақты бұрыш тік, олай болса, бұдан

3-есеп. тетраэдрында .

қырындағы екіжақты бұрыш . мен тетраэдр көлемін табыңыздар.

Шешуі. – тетраэдрдің биіктігі болсын. Онда және бұрышы – қырындағы екіжақты бұрыштың сызықтық бұрышы болады (10-сурет).

10-cурет

Есеп шарты бойынша . Үшжақты бұрыштың қасиетінен,

. Осыдан

үшбұрышынан:

Тік бұрышты ұшбұрышынан , ендеше . Жауабы: ; .

15. Лекция. Математикадағы тексеру жұмыстары. Тест теориясы

Лекцияның мақсаты: Математикадаға тексеру жұмыстарының әдістемесі. Тест теориясы. Білім, білік, дағды, шығармашылық ойлауды дамыту. Қайталау

Қазіргі кезде елімізде өтіп жатқан окытудың мазмұны мен әдістерін қайта құру кезеңінде оқушылардың білім, білік, дағдыларын шынайы тексеру және оларға дидактикалық сипаттама беру көкейтесті мәселелердің біріне айналып отыр. Кез келген адамға білім беруді бастаудан бұрын оның білім деңгейіне диагностика жасап, анықтап алу заңды құбылыс. Себебі дидактикалық диагностика оқытушыға нені және қалай оқыту керектігіне жол сілтейді, әрбір білім алушының деңгейлік сипаттамасын көрсетеді. Балалардың білім деңгейін саралап алмайынша ешбір дифференциалдық оқыту іске асырыла алмайды. Білім берудің әрбір кезеңінен, тіпті сабақтың әрбір кезеңінен екінші кезеңіне өтуде алынған білім, білік, дағдылар мен шығармашылық қабілеттерді, ойлау мүмкіндіктерін тексеріп алмайынша білім берудің ары қарай жүзеге асырылуы мумкін емес. Сондықтан, математикадағы тексеру жұмыстарының маңыздылығы алғашқы оқуды бастайтын кезден көкейтесті мәселелердің бірі болып табылады.

• математика сабақтарындағы тексеру жұмыстарының орнын анықтау;

• математикадан сабақ үрдісінде және сыныптан тыс жұмыстардағы тексеру жұмыстарының оқушылардың білімін жетілдірудегі ролін айқындау;

• Математика сабақтарындағы бақылау, тексеру жұмыстарының түрлерін басқа елдердегі білім деңгейін тексеру жұмыстарымен салыстыру;

• Математика сабақтарындағы тексеру жұмыстары арқылы оқушылардың білімі мен біліктілігін қалыптастырудың тиімді әдістерін жасау.

1. Математикадан білім беру саласындағы бақылау, тексеру түрлері

Тексеру тәсілдері: ауызша (жеке, топтық); жазбаша (диктант, мазмұндама, сынақ, зертханалық жұмыс, бақылау жұмысы); өз бетінше тексеру жұмысы, емтихан.Тексерудің көбі үлкен тақырып, бөлім аяқталғанда жүргізіледі. Әрбір сабақта, сабақтың әр кезеңінде оқушылардың білім, білік, дағдыларын тексеруден басқа, ауызша және жазбаша тексеру жұмыстарына бағытталған бақылау жұмыстарына арналған сабақтар, зачет, емтихан, қабылдау, тест т.б. өткізу қажеттігі туындайды. Сабақ үрдісінде өткізілетін тексеру жұмыстарының бәрін қадағалап отыру үшін тақтаның бір бөлігіне немесе компьютердің белгілі бір файлына әрбір оқушының атын жазып, тұсына қойылған сұрақтарға берген жауаптарын (мысалы, «плюс», «минус», т.б.) белгілеп отырған жөн. Кейде мұғалім оқушылардың өздері белгілеп отыруын ұсынады. Бұл сабақтың соңында білім алушылардың өздерінің білімін өздері бағалауына мұғалімнің қойған бағасы мен білім алушының өзі қойған бағасының ынтымақтастықта қойылуына, бағаларға комментарий жасауға кететін уақытты үнемдеуге септігін тигізеді.

Тексеру жұмыстарының өткізілу уақыты мен оның ұзақтығы оқушыларға алдын ала хабарлауды қажет етеді. Бұл оқушылардың психологиялық бейімделуін қамтамассыз етеді. Бақылау жұмысы немесе емтихан алдындағы қорқыныш сезімдерін жеңуге, стресс ахуалының алдын алуға септігін тигізеді.

Бақылау жұмыстарының материалдарын жасағанда оқытушы қазіргі заманғы техникалық көбейткіш ксерокөшірме, компьютердің проектрлеуші қондырғылардың мүмкіндігін пайдаланып, жұмысын жеңілдеткені жөн. Сонымен бірге осындай тексеру сабақтарының жоспарын жасағанда білім алушылардың білімінің деңгейлік саралануын ескеріп құрылатын тапсырмалардың шешімдері мен жауаптарын сабақ жоспарына міндетті түрде ендіруі тиіс.

Тексеру сабақтарының мынадай түрлері болады: ауызша және жазбаша; оқылған тақырыптан соң бірден алынатын бақылау жұмыстары және біраз уақыт өткізіп барып алынатын бақылау жұмыстары, көп уақыт өткізіп барып алынатын бақылау жұмыстары, яғни уақыт өткен сайын алынған білімдердің беріктігін тексеруге арналған жұмыстар т.б. Олардың дидактикалық мақсаты тек білім деңгейін тексерумен ғана шектелмейді. Тексеру сабақтары білім беру функциясын да атқарады, окушылардың даму деңгейін де анықтайды. Жазбаша тексеру жұмыстары сабақтың бір бөлігіне немесе бүтін бір немесе екі сабаққа есептеліп беріледі. Мазмұнында міндетті бөлікпен қатар математикаға қабілетті оқушылар үшін қосымша бөлігі жоспарланады. Оқушылардың үлгірім деңгейіне байланысты нұсқалар саны көп болғаны, тіпті әрбір білім алушының аты жөні жазылған, арнайы текстер берген тиімді. Оқушы өзінің аты жазылған арнайы тапсырма алғанда, оның жауапкершілігі артып, жұмысқа ықыласпен қарайтыны байқалады. Мұғалім бақылау жұмысында оқушылардың бәрі түгел тиімді жұмыспен айналысуын қадағалап, сұрақтарға жауап береді. Оқушыларды жазылған жұмыстарды уақытында өткізуге үйретеді.

Келесі сабақтың бір бөлігін немесе түгел бақылау жұмыстарын талдауға, жиі кездесетін қателер мен жеке оқушылардың жіберген қателеріне, жұмыста жіберілген грамматикалық, символикалық, логикалық қателеріне талдау жасап, сараптауға арнаудың маңызы өте зор. Бұл осындай қателердің келесі бақылау жұмысында болдырмаудың кепілі бола алады және оқушыларды сауатты жазуға, логикалық ойлауын, сөз байлығын, шығармашылық кабілетін дамытуға ықпал етеді.

Бақылау жұмысын нашар жазған оқушыларға қателерін талдап, көрсеткеннен кейін қосымша нұсқа беріп, бақылау жұмысын қайта жазуға мүмкіндік беріледі. Жазбаша бақылау жұмыстарының тестік тапсырмалардан бір артықшылығы оқушылардың жазу стиліне, математикалық сауатты жазуына, есептерді шығарғанда сөз байлығын пайдаланып, түсініктемелер, тұжырымдар жасауын тексеруге, сол арқылы олардың жазу сауаттылығы мен сөз байлығын, шығармашылық қабілеттерін, логикалық ойлауын тексеруге мүмкіндік беріледі. Ал, тестік тапсырмалар уакытты үнемдеуге, оқушының да, тексерушінің де артық жұмыстарын азайтуға, білім беру функциясын т.б дидактикалық функцияларды іске асыруға мумкіндік береді.

Оқыту өнімділігінің санмен, сапамен, толықтылығымен, деректілігімен, тереңділігімен, әділ бақылаумен тығыз байланыстылығы әдістемелік үрдістің ең жоғарғы заңдылығы ретінде қарастырылады. Оның іс-әрекетке айналып кетуі үшін бақылаудың тиімділігін негіздеп, әсер етуші факторларды ажыратып, түсінікті нақтылау қажет. Қазіргі теорияда әлі “баға”, “бақылау”, «тексеру», «есеп» және осылармен байланыстыларды ажырататын үйлесімділік жоқ. Оларды бір мағынада жиі алмастырып та, қолданып та жүр.

«Бақылау» жалпы шығу түріне қарай оқушының білімін, біліктілігін бағалау мен өлшеуді білдіреді. Өлшеу мен анықтауды тексеру дейді. Сондықтан тексеру – бақылаудың негізгі құрамы, оқушымен оқытушы арасындағы кері байланысты анықтайтын мұғалімнің оқушының нені дұрыс меңгере алмағанын, жіберген кемшілігінен әділ мәлімет беретін негізгі әдістемелік міндеті. Тексеру тек оқушылардың оқытылу сапасы мен деңгейін анықтамайды, сонымен бірге оқыту еңбегінің соңғы көлемін де білдіреді. Бақылау тексеруден басқа бағалау (әрекет ретінде) және тексеру (нәтиже ретінде) бағасын да қамтиды. Баға үлгерім табельдерінде, сынып журналдарында, мәліметтер жинағында т.б. белгі ретінде (шартты белгілердің көрсеткіші, «кескіні», ескерту таңбасы) қойылады.

Оқушылардың үлгерімін бағалау негізі бақылау (нәтижесі) қорытындысы болып табылады. Сонымен қатар оқушы жұмысының сапасы да, саны да ескеріледі. Сандық көрсеткіштерінің артықшылығы пайыз бен балл түрінде, ал сапалық – «жақсы», «қанағаттанарлық» т.б. өлшеммен белгіленеді. Әрбір бағалау пікірге алдын-ала келісілген (белгіленген) ұпай, көрсеткіш (мысалы, «өте жақсыға» – 5 ұпай) қоса жазылады. Мұнда баға тек қана нәтиженің өлшемі мен айқындаушы емес, бағалау пікіріне қосымша мағына үстейтінін түсіндіру керек. Санды қолдан жасап қою бағалау пікірмен қайшылық келтіреді. Әлемнің көптеген елдерінде сандық өлшемге қызығушылықтан сақтану үшін әріптік белгілерді қолданады. Мысалы, А, В, С т.б.

Осы критерий бойынша бағаны анықтау үшін ұсынылған мәліметтер мен игерілгендердің көлемін өлшеуді білу қажет. Бұл міндет ыңғайлы практикалық технология деңгейінде шешілген. Баға қызметі, бізге белгілі болғандай оқытылу деңгейімен ғана өлшенбейді. Баға – педагогтың жеке тұлғаның оқуын реттейтін, жағымды құралы. Әділ бағалау арқылы оқушы бойында өіне-өзі сын көзбен қарауы, өзін бағалауы қалыптасады. Сондықтан бағаның ең басты маңыздылығы, оның қызметінің түрі оқушының оқу әрекетінің барлық жағында оны жан-жақты аша алатындығында. Осы көзқарас негізінде қазіргі білім, біліктілікті бағалауда баға жүйесін диагностикалау маңызымен қоса қайта қарастыру қажет. Оқытуды диагностикалаудың, бақылаудың принциптері болып маңызы әділдік, жүйелілік, көрнекілік (жариялылық) болып табылады.

Әділділік – педагогтың оқытатын шәкірттерінің біліктілігін, білімін диагностикалық тестерді (тапсырмалар, сұрақтар) диагностикалау тәртібін дәл, нақты, өзара түсінікті қатынас арқылы ғылыми негізге арқау ету болып табылады.

Диагностикалаудың практикалық әділдігі диагностикалау көрсеткен педагогтың кез келген бақылау құралдары мен қолданған әдістерімен қойған бағасы үйлесімділік тауып отырады. Бастапқы білімді қабылдаудан бастап, оны практикада қолдануға дейінгі барлық әдістемелік үрдіс диагностикалық бақылау жүргізу – жүйелілік үрдістің түрлері болып табылады. Оқу мекемесінде үнемі жүргізілетін диагностикалау – оқитын шәкірттің бірінші күнінен бастап барлық әрекетін жүйелілікпен қамтиды. Бақылаудың түрлі формалары әдістері мен құралдары, тексерулер, бағалаулар диагностиканы кешенді жүргізуде жүйелілік қағадасын ескеруді талап етеді. Жеке әдістер мен диагностикалау құралдарының жан-жақтылығына назар аударған дұрыс.

Диагностика үрдісінде әр оқушының салыстырмалы, көрнекті рейтингісі шығарылады. Баға – оқушылардың өздеріне деген талап үлгілерін және педагогикалық әділділігін салмақтайтын бағдар. Оқушылардың білік, білімін бағалау, тексеру, бақылау, диагностикалау оны қалай жүргізілетініне де байланысты болады..

Оқушылардың білім деңгейінің алдын ала шығарылған көрсеткіші – тексеру жүйесінің ең бірінші құрамдас бөлігі деп есептеледі. Ол оқу жылының басында оқушының өткен оқу жылындағы білімін анықтау үшін жүзеге асырылады. Алдын ала тексеру біліміндегі, дағдысындағы кемшіліктерді жою мақсатымен сәйкес жүргізіледі. Мұндай тексеру оқу жылының ортасында да, жаңа тарауды бастар алдында да жүргізуге болады. Әр тақырыпты меңгеру үрдісіндегі, ағымдағы бағалар білімді тексерудің екінші құрамдас бөлігі болып табылады. Бірақ ол әр сабақта жүргізілсе де оқушылардың белгілі бір өткен, меңгерген тақырыбы бойынша ғана диагностикалауға мүмкіндік береді. Мұндай тексерулердің әдістері мен формалары оқу материалының мазмұны, оның қиындығы, оқушылардың жас ерекшелігі, дайындық деңгейі, оқыту мақсаты мен көлемі, нақты шарттар сияқты түрлі факторларға байланысты болады.

Ағымдағы бағалар сияқты тақырыптық қайталап тексеру біліктілік пен білімді айқындаудың үшінші құрамдас бөлігі болып табылады.

Оқушылар жаңа тақырыппен қоса бұрын өткен материалды да қайталап оқиды. Қайталап тексеру білімді бекітуге ықпал жасағанымен оқу жұмысының қозғалысын, меңгерілген білімінің беріктік деңгейін диагностикалай алмайды. Диагностикалаудың әдістері мен түрлерін басқаларымен үйлестіре жүргізгенде мұндай тексеру қажетті нәтиже береді. Бұл жүйе құрастырылған бөлім – оқушының бір тарау бойынша немесе курстың маңызды бөлігін білетін білімін кезең бойынша тексеру болып табылады. Мұндай тексерудің мақсаты – оқушының бір курстың әр тарауынан алған білімдерінің сапасын оқу материалымен байланыстыра диагностикалау. Кезеңмен тексерудің негізгі қызметі – жүйелеу және жинақтау. Оқушылардың әдістемелік үрдістің барлық кезеңінде игерген біліктілігімен білімінің есебіне қорытынды тексеру, тексеруді ұйымдастырудың бесінші құрамдас бөлігі болып табылады.

Үлгерімнің қорытындысы есеп әр тоқсан аяғында және оқу жылы аяқталғанда жүргізіледі. Ол алынған бағаларды орташа арифметикалық балға қосып жай ғана есептелмейді. Ол ең алдымен осы кезеңдегі алға қойған мақсат пен нақты оқытылғанның деңгейін диагностикалау. Кешенді тексеру арнайы тексеру түрі болып табылады. Оның көмегімен оқушының игерген білімді басқа пәндерде, практикалық іс-әрекетті шешуде қолдана білу қабілеті диагностикаланады. Мәселен, жеке қожалықтығы құс өсіру шаруашылығының тиімділігінің есебін шығару физикалық, химиялық, математикалық, биологиялық, географиялық және басқа да пәндерден алған білімді қажет етеді.

Кешенді тексерудің басты міндеті – пәнаралық байланыс сапасының жүзеге асырылуын диагностикалау, оқушының құбылысты, үрдістерді, оқиғаларды, тұтас мәліметтерге сүйене отырып, оның ішінде оқылған пәндерінен алған білімін атай отырып түсіндіру қабілеті көбінесе кешенді тексерудің практикалық критерийі болып табылады.