Исследование влияния условий деформирования на прочностные характеристики полимерных материалов при растяжении

Цель работы: изучить влияние условий испытания на деформационные характеристики полимерных материалов.

Приборы и принадлежности: разрывные машина, нож вырубной, вырубной пресс, штангенциркуль.

Предварительная подготовка:

1. Ознакомиться с особенностями различных физических состояний полимерных материалов [1, с. 129 – 131]; [2, с. 68 – 73].

2. Изучить особенности деформационного поведения полимерных материалов в стеклообразования и высокоэластическом состояниях [1, с. 208 – 217]; [3, с. 126 – 183, 185 – 248]; [4, с. 141 – 158].

3. Изучить особенности деформационного поведения кристаллических полимеров [1, с. 217 – 221]; [2, с. 250 – 279]; [4, с. 217 – 237].

Методические указания

1. Общие закономерности процессов деформации полимеров.

Механические свойства полимерных материалов при растяжении обычно исследуют с помощью разных машин, при этом получают зависимость напряжение-деформация, называемую деформационной кривой, при которой определяется фазовым и физическим состояниями деформируемого полимера.

На рисунках 7.1, 7.2 представлены деформационные кривые полимеров в стеклообразном и высокоэластическом состояниях, а также кристаллических полимеров. Как видно из рис. 7.1 деформационные кривые полимеров можно разделить на несколько участков характеризующих различные стадии процесса деформации. Для стеклообразных полимеров рис. 7.1, а, начальная область (область 0а), представляющая собой прямолинейный участок (если температура испытания на несколько десятков градусов ниже температуры стеклования Т_с) соответствует деформации, которая формально подчиняется закону Гука. Модуль упругости твёрдых полимерных материалов на этом участке составляет величину порядка 10⁴ кг/см², т.е. он на 2 порядка меньше модуля упругости стали, однако он в несколько тысяч раз больше модуля упругости (эластичности) тех же полимерных тел, находящихся в высокоэластическом состоянии. Модуль упругости стеклообразных полимеров даже при очень низких температурах, (намного ниже Т_с) не является чисто упругим. Объясняется это релаксационными явлениями, в данном случае деформацией упругого последствия, которая добавляется к упругой деформации и искажает форму зависимости напряжение-деформация. Рассчитанные по наклону линейного участка модули упругости будут несколько заниженными.

Рис. 7.1. Зависимость относительного удлинения ε от напряжения σ (напряжение рассчитано на начальное сечение (I) и на истинное сечение в шейке (II) для:

а – аморфных стеклообразных полимеров;

б – кристаллических полимеров; в – эластомеров

На участок ав наклон кривой растяжения начинает заметно меняться. Это связанно с началом развития в образце вынужденно-элас- тических деформаций. Появление заметной вынужденно-эластической деформации – процесс локализованный; он начинается в наиболее слабом сечение (или в нескольких сечениях) образца. Скорость развития вынужденно-эластической деформации очень чувствительна к напряжениям, поэтому если какое-либо сечение образца хоть немного ослаблено (ослабление сечения может произойти не только за счёт небольшого сужения, но и вследствие неоднородности в надмолекулярной структуре материала), то небольшого повышения напряжения в нем достаточно для резкого ускорения вынужденной эластичности. Затем, когда скорость развития вынужденно-эластической деформации сравняется со скоростью деформации, задаваемой разрывной машиной, напряжение перестает расти, и на криво растяжения образуется максимум. Величина этого максимума характеризует условную величину – предел вынужденной эластичности, обозначает σ_в7. Иногда при растяжении стеклообразных полимеров максимума на кривой растяжения не наблюдается. В таких случаях предел вынужденной эластичности можно определить по точки пересечения касательных к двум ветвям кривой растяжения. В момент прохождения напряжения через максимум на рабочей части образца начинает образовываться шейка и происходит побеление материала в ней, связанное с образованием макроскопических разрывов.

После прохождения через точку максимум напряжение в образце уменьшается (участок вс) и к концу напряжения формирование шейки заканчивается. Можно назвать много причин, вызывающих спад напряжения в образце: быстрое уменьшения сечения в шейке, нагрев материала, образование макроразрывов и т.д. Если построить кривые растяжения при расчёте на истинное сечение, тщательно его измерил на всех стадиях образования шейки, можно убедиться или совсем прекращается рис. 7.1, а, кривая 2. Если напряжение рассчитано на начальное сечение, образование максимума на кривой растяжения обусловлено, главным образом, сужением образца в шейке.

Особый интерес представляет участок cd кривой растяжения (рис. 7.1, а, кривая 1). На этом участке напряжение остается практически постоянным, а удлинение образца происходит за счёт вынужденно-эластической деформации у границ шейки. Материал переходит из толстой, недеформируемой части в тонкую шейку. В точке d рост шейки прекращается. Область de соответствует дальнейшей деформации образца уменьшенного сечения, напряжение на этом участке снова начинает возрастать.

Типичная кривая нагрузка-удлинение кристаллических полимеров рис. 1б оказывается практически такой же, как и соответствующая кривая аморфных полимеров. На деформационной кривой кристаллических полимеров также можно выделить три отчётливо выраженных участка. Переход от первой стадии растяжения ко второй для кристаллических полимеров выражается более резким перегибом, чем в случае проявления вынужденной эластичности для аморфных полимеров. Деформация кристаллических полимеров имеет свои характерные отличия по сравнению с деформацией аморфных полимеров, особенно в молекулярном механизме явлений, что следует помнить при работе с кристаллическими полимерами.

На участке 0а усилие, прилагаемое к образцу, пропорционально усилию и возникающая деформация, как правило, обратима. Величина модуля на этой стадии ниже модуля растяжения, кристаллических низкомолекулярных тел благодаря тому, что значительная часть полимера является аморфной и общая деформация является главным образом деформацией аморфных микрообластей полимера. На первой стадии не происходит перестройки структуры материала, он деформируется как единое целое.

Определять модуль упругости по тангенсу угла наклона первого участка криво растяжения не всегда удается. Поэтому вводят условный модуль, определяя его как отношение напряжения σ при некоторой деформации ε к величине этой деформации. Обычно величина ε составляет несколько процентов, так как этой деформацией и ограничивается первым участком кривой растяжения. Величину деформации ε можно принимать произвольно, но сравнивать модули упругости различных полимеров нужно только при строго одинаковой деформации. В тех случаях, когда линейность на первом участке соблюдается, поступают как обычно, – вычисляют тангенс угла наклона этой линии к оси абсцисс.

Когда напряжение достигает величину σ_рекр, в образце возникает шейка, при этом наиболее слабые кристаллиты начинают интенсивно разрушаться, как бы плавиться под действием механических сил. На этой стадии растяжения – участок ав – в исходном образце кристаллического полимера при постоянном напряжении происходит процесс рекристаллизации – плавление одних кристаллов и создание других, ориентированных в направлении растяжения и поэтому более прочных. На второй стадии деформации удлинение не исчезает после снятия нагрузки, величина его несколько сотен процентов.

Такое скачкообразное превращение кристаллических областей из одной формы в другую имеет все признаки фазового перехода. Процесс рекристаллизации заканчивается в точке в, при этом весь образец переходит в шейку.

Участок вс соответствует удлинению шейки, которая растягивается как единое целое вплоть до разрыва., причем величина деформации на этом участке больше, чем на участке 0а.

Типичная кривая зависимости относительной деформации от напряжения при простом растяжении каучукоподобных полимеров (эластомеров) представлена на рис. 7.1, в (S-образная кривая). Из рисунка видно, что закон Гука соблюдается только при малых деформациях, т.е. на первом участке. На втором участке малым изменениям напряжения соответствует большие деформации (высокоэластическая деформация). Третий участок отвечает резкому возрастанию напряжения при незначительном изменении деформации, что обусловлено изменением структуры материла. На втором участке модуль упругости не является постоянной величиной, ео значение зменяется в зависимости от величины напряжения. Однако, практически для всех напряжений модуль упругости эластомеров мал и величина его того же порядка, что и у газов, т.е. он примерно равен 2 кг/см² (0,2 МПа). Отсюда возникает положение о кинетической природе высокой эластичности полимеров.

2. Влияние различных факторов на деформационные свойства.

Вид деформационной кривой полимерных материалов в значительной степени определяется температурой, при котором проводится испытание и скоростью механического воздействия. Меняя температуру в широком интервале можно для одного и того же полимера получать самые разнообразные типы кривых деформации.

Рис. 7.2. Типы кривых нагрузка-удлинение полимеров при различных температурах:

1 – при температуре выше Т_т; 2 – при температуре, соответствующей высокоэластическому состоянию; 3 – при температуре меньше Т_ст для аморфных и меньше Т_кр для кристаллических полимеров; 4 – при температуре ниже Т_хр

Величины σ_вэ и σ_рекр возрастают при понижении температуры и может наступить такой момент, когда они превысят прочность материала на разрыв. В этом случае деформационная кривая вырождается, и раньше, чем начнется процесс образования шейки, образец разрушиться (кривая 4, рис. 7.2). С повышением температуры испытания максимум на деформационной кривой постепенно сглаживается, а образование шейки наступает при всё больших деформациях. Эти же эффекты наблюдаются при изменении скорости деформирования. Увеличение скорости деформирования по своему воздействию аналогично снижению температуры, а её уменьшение – повышению температуры испытания. Это и есть одно из ярких проявлений принципа температурно-временной суперпозиции – эквивалентности влияния температуры и времени воздействия.

Огромное влияние на деформационные свойства полимеров оказывает на их молекулярный вес. Влияние молекулярного веса на деформацию весьма своеобразно. Диаграммы растяжения полимеров с различными молекулярными весами в точности накладываются друг на друга, но по мере снижения молекулярного веса укорачивается по оси удлинений (рис. 7.3).

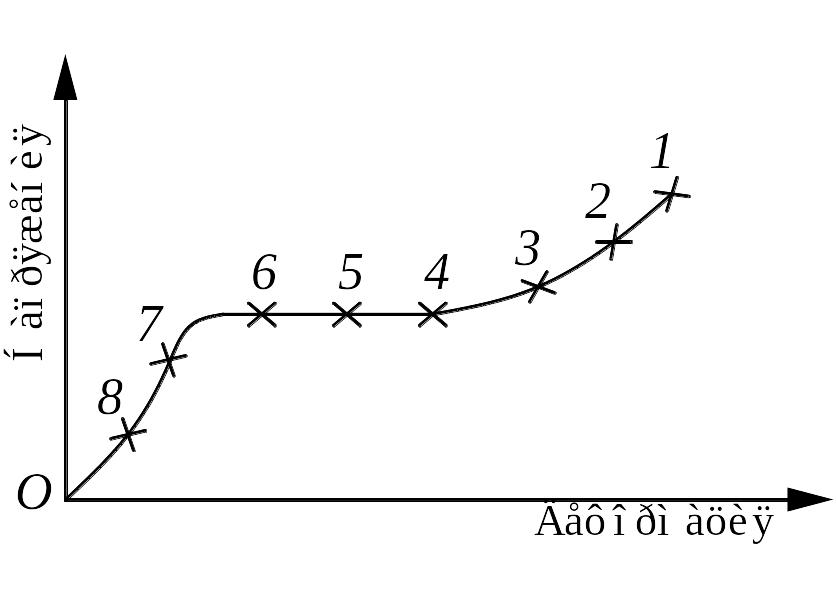
Рис. 7.3. Деформационная кривая полимеров с различным молекулярным весом

Точки на кривой соответствуют окончанию процесса деформирования (разрыву) полимеров различного молекулярного веса. В общем случае деформация образцов в момент разрыва постепенно перемещается на деформированной кривой с третьего на второй, а затем и на первый участок, что соответствует хрупкому разрыву. Низкомолекулярный полимер утрачивает одну их характерных особенностей высокополимерных веществ – способность к чрезвычайно большим деформациям. Наоборот, повышение молекулярного веса полимера приводит к резкому изменению механических свойств – снижению хрупкости и развитию больших деформаций.