Контрольные вопросы

1. Основные закономерности процесса кристаллизации полимеров.

2. Какое влияние оказывает температура и скорость охлаждения на процесс кристаллизации полимеров.

3. Что понимается под надмолекулярной структурой полимеров?

4. Какие типы надмолекулярных структур присущи кристаллизующимся полимерам в зависимости от условий кристаллизации?

5. В чем заключаются особенности надмолекулярной структуры аморфных полимеров?

Рекомендуемая литература

1. Джейл, Ф.Х. Полимерные монокристаллы / Ф.Х. Джейл. – Л. : Химия, 1968. – 552 с.

2. Торнер, P.В. Теоретические основы переработки полимеров / P.В. Торнер. – М. : Химия, 1978.

3. Манделькерн, Л. Кристаллизация полимеров / Л. Манделькерн. –

4. Новейшие методы исследования полимеров / под ред. Б. Ки. –М. : Мир, 1966. – 571 с.

Лабораторная работа 6

Изучение ползучести полимеров в твёрдом состоянии

Цель работы: снять кривую ползучести-восстановления полимерного материала и определить постоянные реологического управления; построить изохронную кривую растяжения и определить релаксационный модуль упругости; определить деформационную долговечность; построить изохронные термомеханические кривые и определить зависимость температуры стеклования от времени воздействия нагрузки.

Приборы и принадлежности: установка для испытания полимеров на ползучесть, микрометр, штангенциркуль, секундомер.

Методические указания

Для измерения характеристик ползучести образец подвергается нагружению до заданного напряжения σ после чего под действием этого постоянного напряжения в нём развивается деформация. В результате определяется зависимость относительной деформации от времени t при σ = const, которую называют кривой ползучести. На рисунке 6.1 представлена кривая ползучести-восстановления полимеров в твёрдом состоянии при напряжениях заметно ниже предела текучести. После приложения напряжения деформация развивается мгновенно до величины OА затем развитие деформации во времени выражается кривой АВ, переходящей в прямую ВD. Участок ОА соответствует небольшой по величине деформации ε₀ , которая формально подчиняется закону Гука и называется условно упругой деформацией.

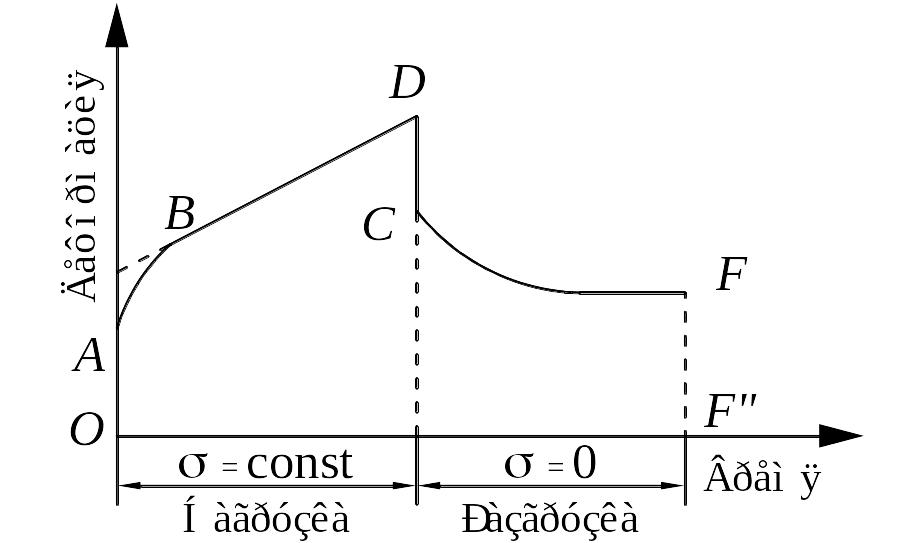
Рис. 6.1. Кривая ползучести-восстановления

Участок АВ – это участок неустановившейся ползучести. Он характеризует одновременно развивающиеся во времени высокоэластическую деформацию и деформацию течения. Прямая ВD связана только с процессом установившегося течения.

На кривой разгрузки (восстановления) отрезок DC, равный по величине отрезку ОA соответствует мгновенному обратимому восстановлению длины образца. Дальнейшее изменение длины происходит во времени постепенно, что соответствует высокоэластической деформации. После прекращения изменения длины образца, отрезок FF» соответствует остаточной, деформации. Природа остаточной деформации после разгрузки может быть двоякой. Остаточная деформация может представлять собой либо деформацию вязкого течения, либо необратимую при данной температуре часть высокоэластической деформации. Кривая изменения деформации во времени в процессе нагрузки называется прямым последствием, кривая разгрузки – обратным последствием.

Кривые ползучести реальных полимерных материалов с достаточной степенью точности могут быть описаны с помощью трёхэлементной реологической модели Максвелла-Томсона, вид которой представлен на рис. 6.2.

Рис. 6.2. Трёхэлементная модель Максвелла-Томсона

Деформационное поведение модели Максвелла-Томсона, описывается уравнением

σ + τσ = Eε + τHε, (4.1)

где τ, H, E – реологические константы уравнения Максвелла-Томсона, для данного материала: – время релаксации; – приведённый модуль упругости; Н = Е₂ – мгновенный модуль упру- гости.

Решение уравнения 4.1 для случая прямого последействия принимает вид:

, (4.2)

а для случая обратного последействия

, (4.3)

где ε₁ – деформация в момент разгрузки; t₁ – время в момент разгрузки; ε_м = σ / Н – мгновенная начальная деформация.

Постоянные реологические уравнения 4.1 определяются по экспериментальной кривой ползучести используя метод академика Малмейстера, согласно которому, решая уравнение 4.2 для случая прямого последействия получим

, (4.4)

, (4.5)

, (4.6)

где ε₁, ε₂ – деформации на кривой ползучести к моментам времени наблюдения t и 2t; – деформация на кривой ползучести, соответствующая времени наблюдения; ε_∞ = σ / E – равновесная деформация образца.

Практически бывает трудно из экспериментальных кривых определить значения ε_м и ε_∞ имеется только наиболее достоверная средняя часть кривой ползучести. В этом случае экстраполяцией кривой ползучести по обе стороны среднего участка получают Б первом приближении значения ε_м и ε_∞. Подставляя эти значения в уравнение 4.6 определяют значения τ по координатам ε(t) и t любых двух, трёх точек кривой ползучести. Если ε_м и ε_∞ выбраны правильно, то значения τ должны совпадать по величине. Путём нескольких попыток следует подобрать искомые значения ε_М и ε_∞, а затем по ним по соотношениям 4.4 и 4.5 подсчитать величины E и H. Если к твёрдому полимеру приложить напряжения, близкие к значению предела текучести σ_т , то кривые ползучести принимают форму, показанную на рис. 6.3. На этой кривой существенный интерес представляет время t_ф, предшествующее моменту резкого ускорения деформации под действием постоянного напряжения. Повышение скорости ползучести t_ф связывают с разрушением исходной структуры полимера вынужденно-эластической деформации.

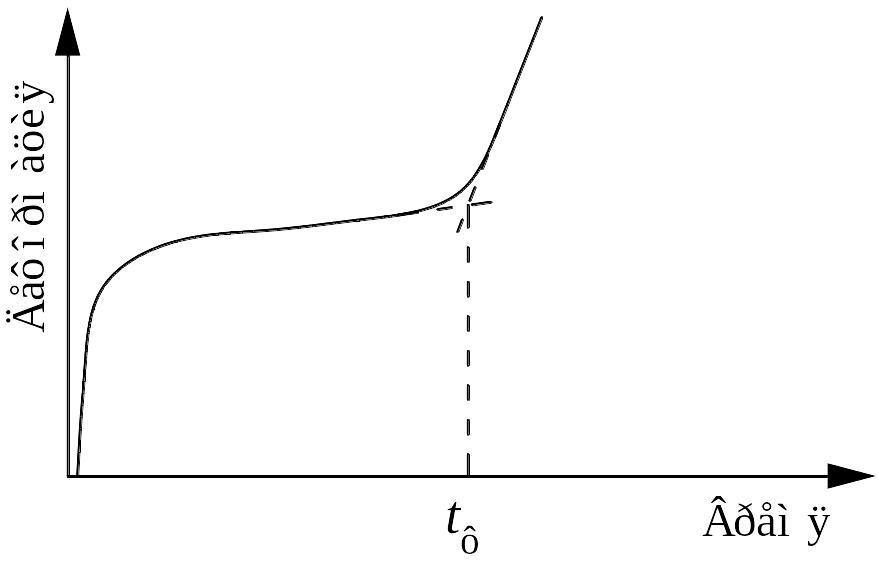
Рис. 4.3. Кривая ползучести при наличии участка быстро возрастающей деформации

Время t_ф называется временем сохранения формы материала и зависит от приложенного напряжения и температуры. Для определения величины t_ф предложен ряд соотношений, одно из которых, предложенное С.Б. Ратнером, имеет вид:

, (4.7)

где t_о – предэкспоненциальный множитель; U_о, , – константы материала; Т_n – имеет смысл температуры полюса, из которого исходит веер прямых в координатах lgt_ф – 1/T.

Набор кривых ползучести, полученных при разных напряжениях, при постоянной температуре T = const позволяет построить так называемые изохронные кривые в координатах σ–ε (рис. 6.4). Каждая точка на кривой отвечает деформации, которая развивается за время t при соответствующем напряжении. Начальный участок изохронной кривой является прямолинейным; при деформациях порядка 0,5…1,0% прямая линия переходит в кривую. По тангенсу угла наклона определяют релаксационный модуль упругости

E(t) = σ / ε. (4.8)

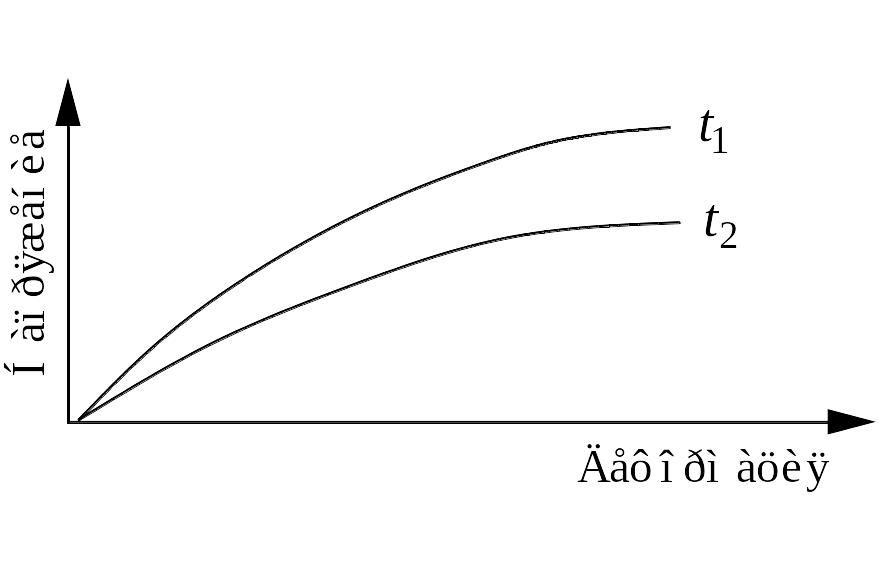
Рис. 6.4. Изохронные кривые растяжения для различных времен нагружения (t₁ < t₂) при T = const

По кривым ползучести, построенным при разных температурах можно построить изохронные термомеханические кривые. Для этого на чертеже семейства кривых, полученных при различных температурах, но постоянной нагрузке проводят вертикали, соответствующие различным временам и строят зависимости ε–Т для выбранного значения времени. По изохронной термомеханической кривой определяют температуру стеклования Т_с для каждого времени t. Затем в координатах Т_с–t строят график зависимости Т_с от времени воздействия нагрузки (с увеличением продолжительности действия нагрузки значения Т_с полимера понижаются).