Уравнивание поправок направлений

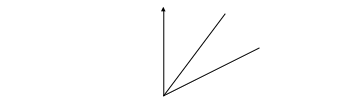
Выразим ошибки направлений через ошибки координат. На рисунке ориентирующий угол, т.е. угол между направлением ix и направлением i0 нулевого диаметра лимба

,

где α_ik – дирекционный угол направления ik, N_ik – уравненное значение этого направления. Принимая

,

находим

, (1)

где , N’_ik – измеренное значение направления.

Продифференцировав выражение по всем переменным, после перехода к конечным приращениям получим

.

Учитывая , имеем

, (2)

или

.

Подставляя полученное выражение в формулу (1), находим

, (3)

где δz_i – поправка в ориентирующий угол z₀ на i-том пункте, ξ_i , η_i , ξ_k , η_k – поправки в дециметрах в приближенные координаты x_i⁰ , y_i⁰ ; x_k⁰ , y_k⁰ пунктов i и k, т.е. ξ = 10δx , η = δy ; δx, δy – поправки в метрах.

Коэффициенты a_ik , b_ik определяют по формулам

(4)

Для обратного направления k-i

, (5)

причем a_ik = -a_ki , b_ik = -b_ki , что служит контролем вычислений. Для исходных пунктов поправки ξ и η равны нулю.

Следует заметить, что ошибки, допущенные при составлении уравнений поправок, обнаруживаются только в конце вычислений, поэтому определение a_ik , b_ik , l_ik нужно контролировать.

Уравнение поправок дирекционных углов

От азимутов Лапласа переходят к дирекционным углам направлений, в которые определяют поправки из уравнивания геодезической сети. Уравнения поправок дирекционных углов отличаются от поправок направлений отсутствием поправки –δz₀ в ориентирующий угол.

Уравнения поправок измеренных сторон

В геодезической сети могут быть измерены стороны, в которые после редуцирования на плоскость проекции Гаусса-Крюгера определяют с учетом весов измерений поправки из уравнивания. Длину стороны s_ik можно определить дважды:

, (6)

где s’_ik – измеренная и редуцированная на плоскость длина стороны; v_ik – поправка из уравнивания; s⁰_ik – длина той же стороны, определенная по приближенным координатам пунктов; δs_ik – поправка в ее значение из уравнивания.

Из формулы (6) находим исходное уравнение поправок измеренных сторон

, (7)

где .

Продифференцировав выражение по всем переменным, имеем

.

Разделив обе части равенства на s⁰_ik , после перехода к конечным приращениям находим

.

После подстановки этого значения в (6), принимая

,

(ξ , η – в дм, δx , δy – в м), получим

. (8)

Составление редуцированных нормальных уравнений

Учитывая, что на каждом пункте сумма поправок v_ik в измеренные направления равна нулю ([v] = 0), можно составить редуцированные нормальные уравнения, в которых поправки δz₀ в ориентирующие углы z₀ исключены. При этом общее число нормальных уравнений уменьшается на число пунктов, на которых измерены направления.

Положим, что на пункте I измерено n направлений, им соответствуют уравнения поправок

Примем и т.д. С учетом этих обозначений

(9)

Переходя к нормальным уравнениям, получим

(10)

Из первого уравнения, учитывая [v] = [l] = 0 , имеем

. (11)

Подставляя полученное значение δz₀ в систему (9), получим части редуцированных нормальных уравнений на данном пункте:

в которых δz₀ исключены.

Общую систему редуцированных нормальных уравнений в сети получают суммированием коэффициентов при одноименных неизвестных поправках в уравнения по станциям. Из решения этой общей системы уравнений находят поправки ξ_i и η_i к приближенным координатам определяемых пунктов. Число поправок, как и общее число редуцированных нормальных уравнений, равно удвоенному числу определяемых пунктов.

После определения ξ_i и η_i по формуле (11) вычисляют δz₀ и по формуле (8) – поправки v_ik . На каждом пункте Σv = 0 , что является контролем правильности вычислений. Уравненные координаты

.

Кроме того, x и y можно определить из решения треугольников, в которых используют уравненные направления.