Кинематические показатели движения точки

Координаты		Скорость, м/с			Ускорение, м/с2					Радиус кривизны, м
-0,06	0	0	0,0628	0,0628	0,493	0	0,493	0,493	0	0,008

Изобразим на графике траекторию точки и покажем векторные величины (рис.3.1).

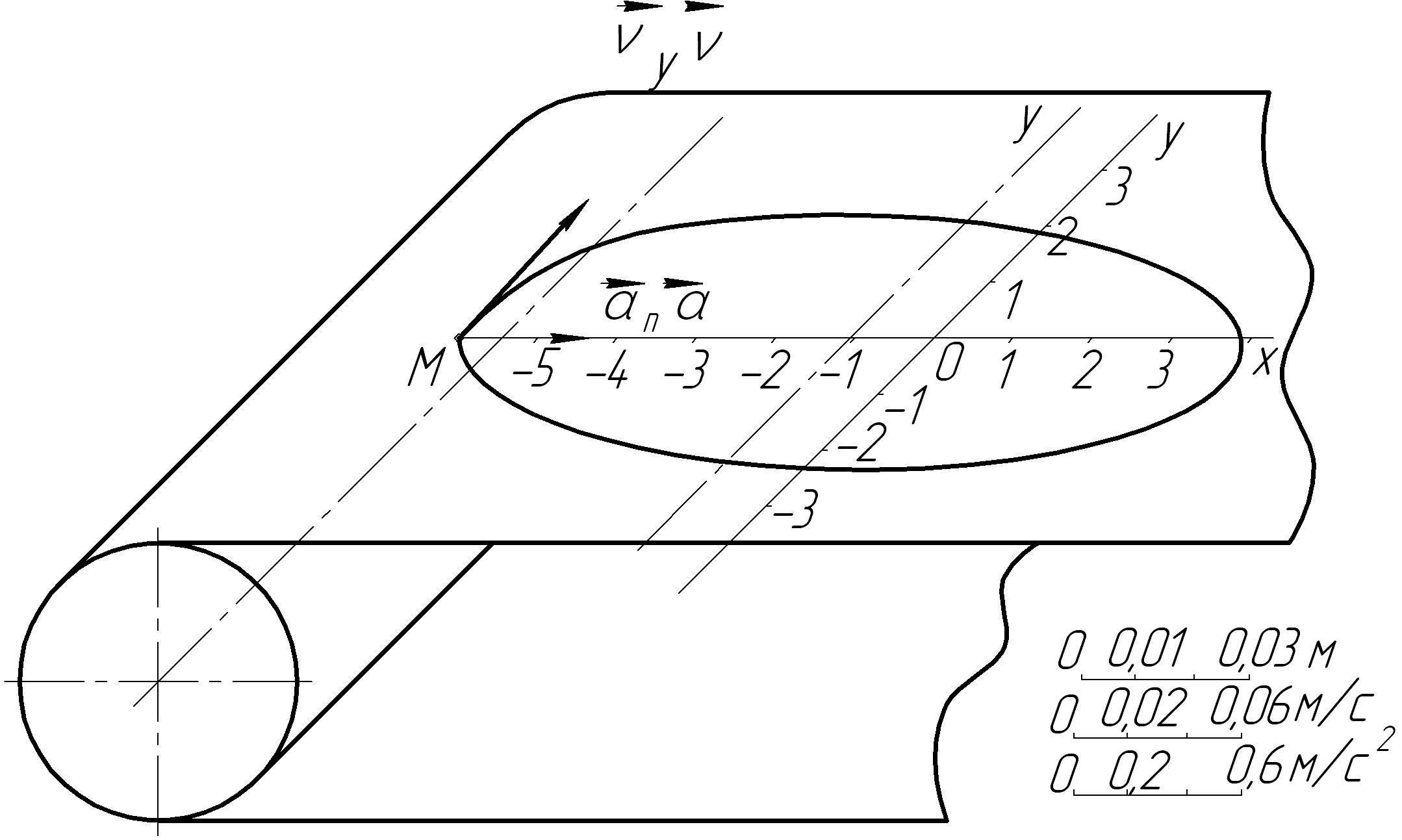
Рис.3.1. Схема исполнительного органа ленточного конвейера и

траектория движения точки

4. Задание к-2:

ОПРЕДЕЛЕНИЕ АБСОЛЮТНОЙ СКОРОСТИ И

АБСОЛЮТНОГО УСКОРЕНИЯ ТОЧКИ

В СЛОЖНОМ ДВИЖЕНИЯ

Для расчета используются схемы согласно рисункам 1.1 1.10 и геометрические параметры, сведенные в таблицу 3.1. Для заданной расчетной схемы и по заданным уравнениям относительно движения точки и переносного движения машины определить для заданного момента времени абсолютную скорость и абсолютное ускорение точки. Уравнение движения, момент времени и положение точки задаются таблицей 4.1.

Таблица 4.1

Исходные данные к К-2

№ варианта	Начальное положение точки	Уравнение переносного движения	Уравнение относительного движения	Время,с
1	2	3	4	5
1	Режущая кромка отвала	,м	,рад	2,3
2	Нижняя точка торца коронки	,м	,с-1	2,1
3	Верхняя точка режущей поверхности коронки	,м	,с-1	1,3
4	Режущая кромка ковша	,рад	,рад	0,1
5	Верхняя точка поверхности фрезы	,м	,рад	3,0
6	Режущая кромка ковша	,рад	,м	1,3
7	Нижняя точка большого диаметра фрезы	,рад	,с-1	1,9
8	Верхняя точка поверхность барабана	,рад	,м	1,6
9	Передняя точка боковой стенки ковша	,рад	,м	0,2

Продолжение табл. 4.1

1	2	3	4	5
11	Передняя точка днища ковша	,рад	,рад	0,13
12	Нижняя точка большого диаметра фрезы	,рад	,с-1	2,2
13	Нижняя точка торцовой поверхности коронки	,м	,рад	2,2
14	Передняя точка боковой стенки ковша	,рад	,м	0,1
15	Режущая кромка отвала	,м	,м	2,5
16	Нижняя точка режущей кромки коронки	,м	,с-1	0,3
17	Нижняя точка режущей кромки фрезы	,м	,рад	1,2
18	Верхняя точка режущей поверхности барабана	,рад	,м	1,5
19	Режущая кромка ковша	,рад	,м	0,3
20	Режущая кромка ковша	,рад	,рад	0,1
21	Режущая кромка боковой стенки ковша	,рад	,м	0,3
22	Крайняя верхняя точка торцовой поверхности фрезы	,м	,м	1,7
23	Центр тяжести фрезы	,м;	,рад	1,2
24	Режущая кромка ковша	,рад	,рад	0,13
25	Задняя кромка днища ковша	,рад	,рад	0,2
26	Верхняя точка режущей поверхности коронки	,рад	,с-1	1,7
27	Верхняя точка режущей коронки	,м	,с-1	1,3

Окончание табл. 4.1

1	2	3	4	5
28	Режущая кромка отвала	,м	,м	1,7
29	Верхняя точка меньшего диаметра фрезы	,рад	, с-1	1,3
30	Нижняя точка режущей поверхности барабана	,рад	,м	2,2

ПРИМЕР 4

В ряде случаев движение точки рассматривают как сложное, состоящее из нескольких движений. Подобных примеров в окружающей нас действительности очень много. Отсюда возникает необходимость изучения сложного движения в зависимости от составляющих его простых движений. Движение материальной точки, отнесенное к неподвижным осям координат, будем называть абсолютным. Движение материальной точки относительно подвижной системы координатных осей будем называть относительным. Движение подвижной системы осей относительно неподвижной называется переносным.

По аналогии с этим в механику вводят понятия скоростей соответствующих движений.

Абсолютной скоростью ( ) называется скорость точки в ее абсолютном движении. Относительной ( ) называется скорость точки, наблюдаемая в ее движении относительно подвижных осей. Под скоростью переносного движения ( ) понимают скорость той точки среды, неизменно связанной с подвижной системой отсчета, с которой в данный момент движущаяся точка совпадает.

Изучим движение точки , принадлежащей ленточному транспортеру, совершающему поступательное движение. По заданным уравнениям относительного движения точки ,м; ,м по поверхности ленты транспортера и переносного движения барабана с радиусом (рис.4.1) определить для момента времени абсолютную скорость и абсолютное ускорение точки.

Определим положение точки на поверхности ленты в данный момент времени:

;

.

Абсолютная скорость точки определяется геометрической суммой относительной и переносной скоростей:

.

Модуль относительной скорости определится как:

;

где ;

.

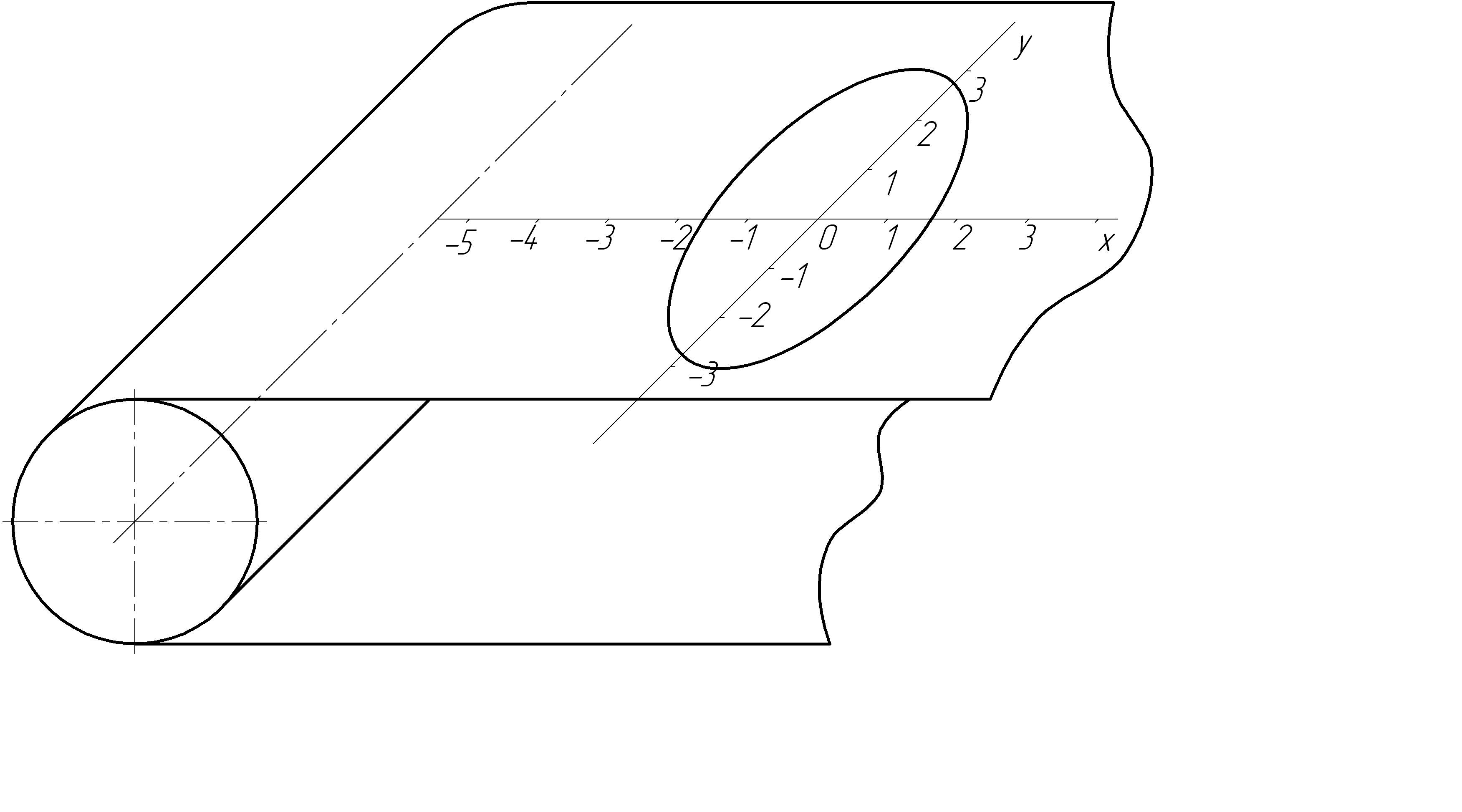
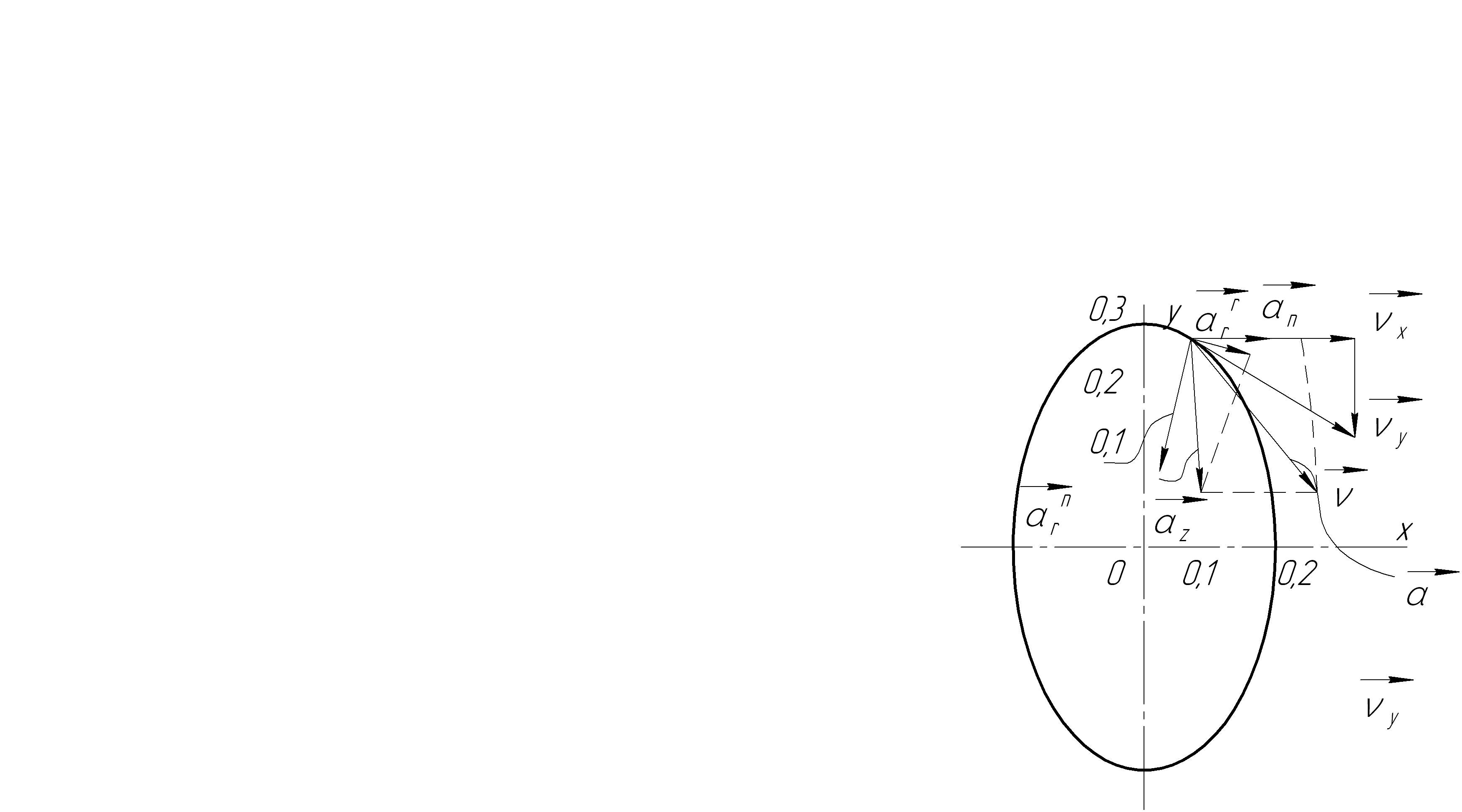
Рис.4.1. Схема исполнительного органа ленточного конвейера

и кинематические показатели сложного движения

Тогда:

.

Углы, образованны вектором относительной скорости и координатными осями:

;

.

Модуль переносной скорости найдем в виде произведения:

.

Вектор переносной скорости направлен по касательной к шкиву, т.е. вдоль оси .

Модуль абсолютной скорости точки определим как совокупность составляющих и :

.

Для этого спроектируем векторное равенство на координатные оси:

;

.

Таким образом:

.

Для определения ускорения точки воспользуемся выражением:

.

Вектор переносного ускорения имеет величину:

,

и направлен вдоль оси .

Определим модуль полного относительного ускорения:

;

где ;

.

Следовательно:

.

Определим касательное относительное ускорении по модулю:

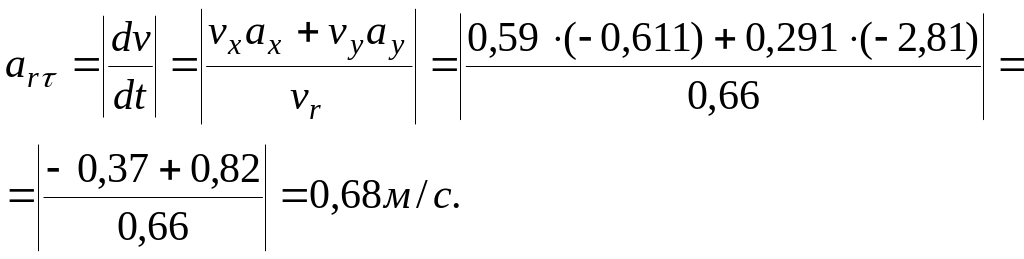
Тогда величина нормального ускорения:

.

Найдем угол между радиусом - вектором точки и осью :

.

Спроектируем векторное равенство на координатные оси, учитывая, что вектор нормального ускорения направлен вдоль радиуса – вектора к центру кривизны траектории, а вектор касательного ускорения ему перпендикулярен:

.

В этом случае величина полного ускорения точки равна:

.

Полученные результаты изобразим графически на рис.4.1 с учетом знаков перед соответствующими проекциями скорости и ускорения.