Исходные данные

АВ, м	ВС, м	СД, м	q1, кн/м	q2, кн/м	q3, кн/м	q4, кн/м
2,5	3,0	2,2	3	2,5	3,4	2,0

РЕШЕНИЕ

Заменим действие распределительных нагрузок сосредоточенными силами. Эпюра распределительной нагрузки, действующей на звено , представляет собой прямоугольный треугольник. Величина эквивалентной сосредоточенной силы равна . Точка ее приложения определится . Эпюра распределенной нагрузки, действующей на звено ВС, представляет собой прямоугольник. Величина эквивалентной сосредоточенной силы равна . Точка ее приложения определится . Эпюра распределенной нагрузки, действующей на звено СD, представляет собой трапецию. Для удобства замены ее действия эквивалентной силой разобьем эпюру на два участка – прямоугольник РОde и прямоугольный треугольник ОРf. Величина силы, эквивалентной прямоугольной эпюры, равна . Точка ее приложения определится . Величина силы, эквивалентной треугольной эпюры, равна . Точка ее приложения определится .

Освободим систему от внешних связей и заменим их действия реакциями. Внешней связью для системы является гладкая горизонтальная поверхность. Ее реакцию представим , перпендикулярной поверхности и приложенной в точке . Другой внешней связью является вертикальная гладкая поверхность. Заменим ее действие горизонтальной реакцией в точке .

Составляем расчетную схему (рис.2.12) и выбираем систему координат .

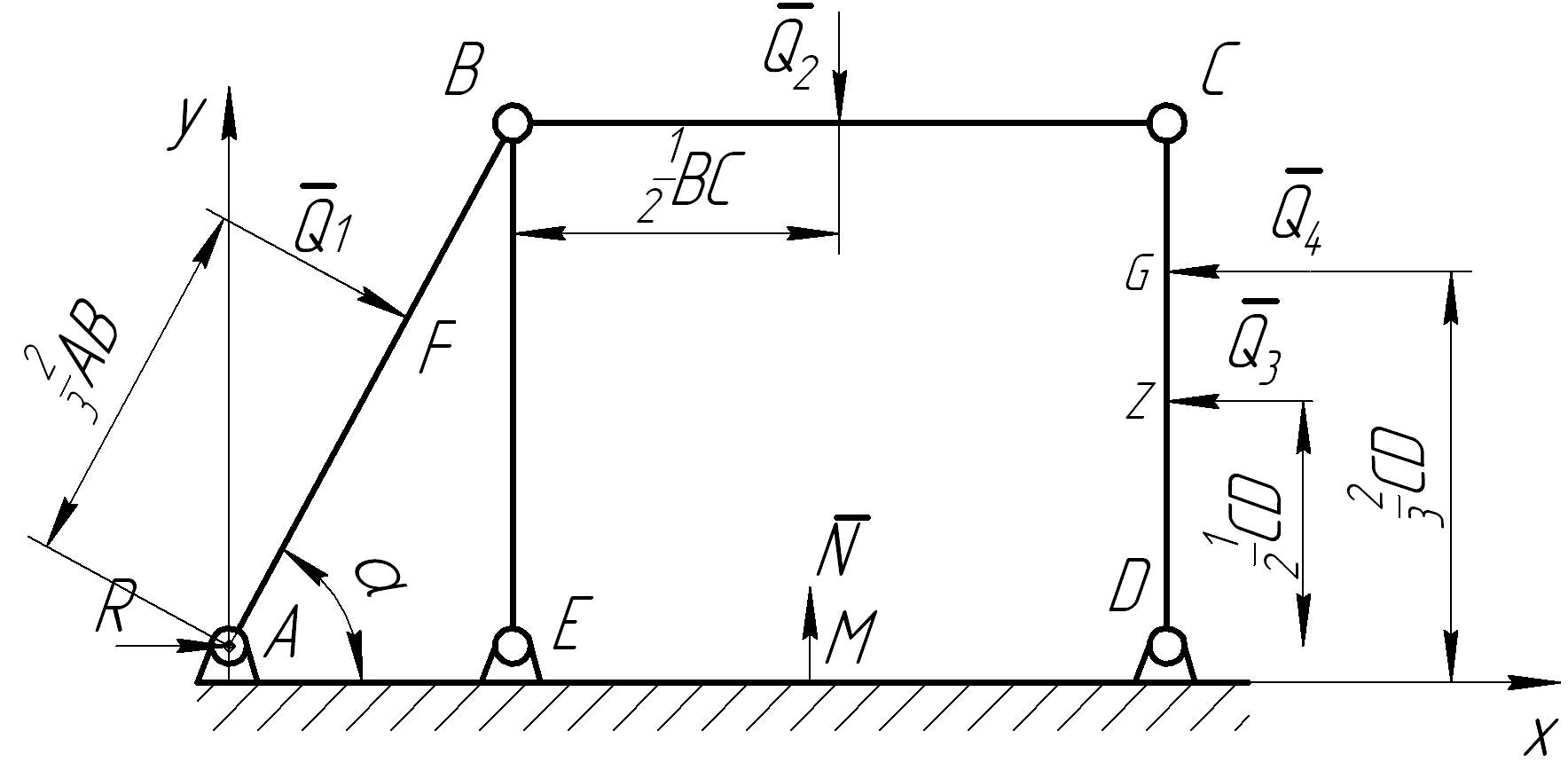
Рис.2.12. Расчетная схема секции крепи.

Получена плоская произвольная система сил. Для определения опорной реакции в точке ее приложения составим условие ее равновесия:

.

Составим сумму моментов всех сил относительно точки :

. (2.1)

Составляем сумму проекций всех сил, действующих на систему, на координатные оси:

(2.2)

(2.3)

Получена система трех уравнений (2.1), (2.2), (2.3) с тремя неизвестными , и . В этой системе

;

Решение системы дает следующее:

.

Из уравнения (2.2):

Из уравнения (2.3):

.

Из уравнения (2.1):

.

Произведем проверку вычисленных величин. Для этого составим сумму моментов всех сил, действующих на систему, относительно точки  :

Определение реакций в шарнирах проведем методом расчленения. Выделим из системы тело и составим для него расчетную схему (рис.2.13), представив реакции в шарнирах составляющими .

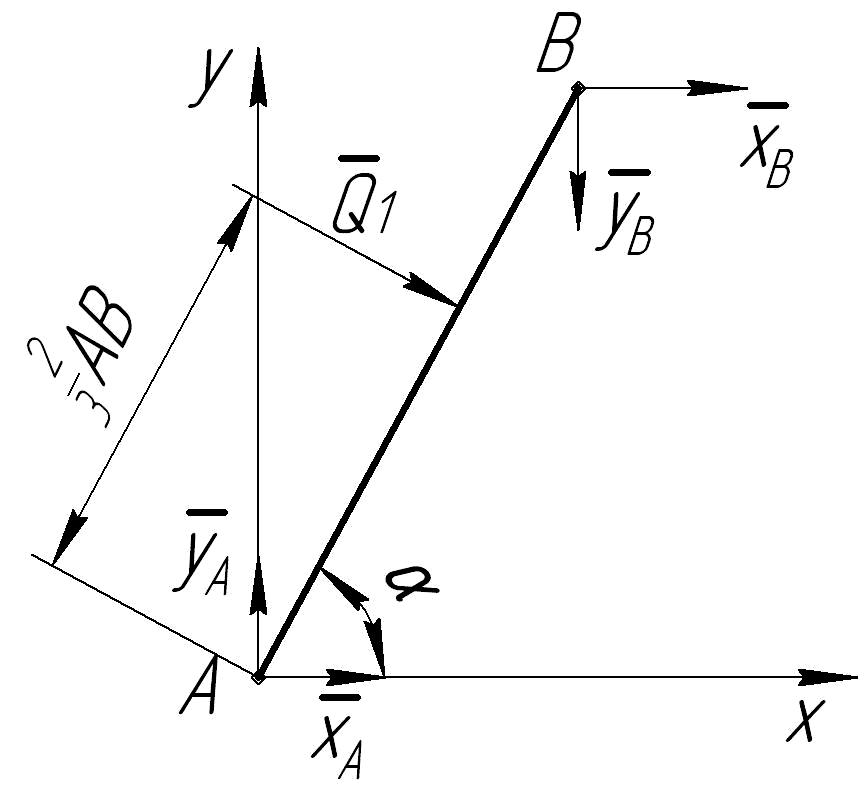
Рис.2.13. Расчетная схема

Получена плоская произвольная система сил. Составим для нее уравнения равновесия:

(2.4)

(2.5)

. (2.6)

Система трех уравнений (2.4), (2.5) и (2.6) имеет четыре неизвестные.

Выделим из системы тело и составим для него расчетную схему (рис.2.14). При этом составляющие реакции в шарнире равны по величине составляющим в том же шарнире для тела , но противоположны по направлению.

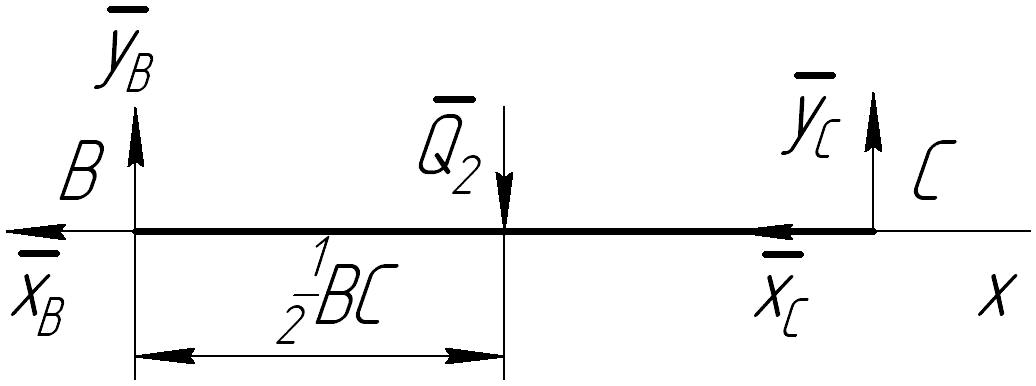
Рис.2.14. Расчетная схема

Получена произвольная плоская система сил. Составляем уравнения равновесия:

(2.7)

(2.8)

. (2.9)

Система уравнений (2.7), (2.8), (2.9) имеет четыре неизвестные.

Выделим из системы тело . Расчетная схема для него имеет вид (рис.2.15).

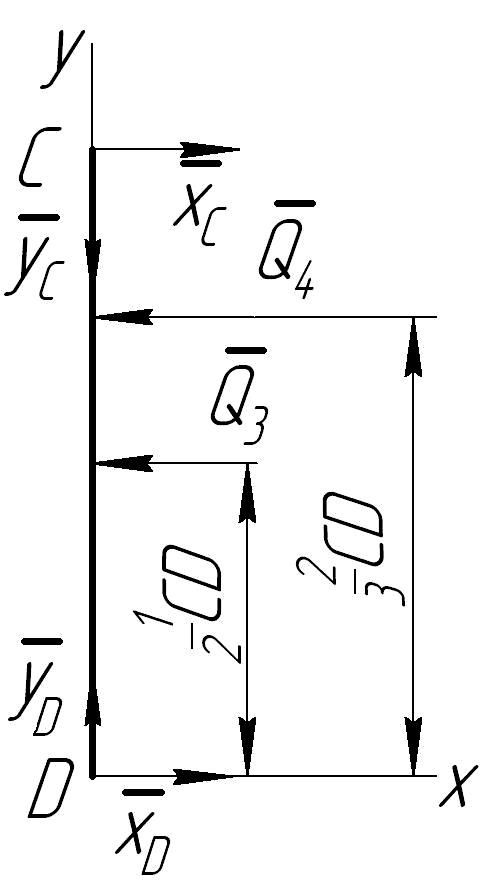
Рис.2.15. Расчетная схема

Имея в виду, что составляющие реакции шарнира направлены в стороны, противоположные аналогичным составляющим для тела , составим уравнения равновесия:

(2.10)

(2.11)

. (2.12)

Система уравнений (2.10), (2.11), (2.12) имеет четыре неизвестные.

Выделим из системы тело . Расчетная схема для него примет вид (рис.2.16).

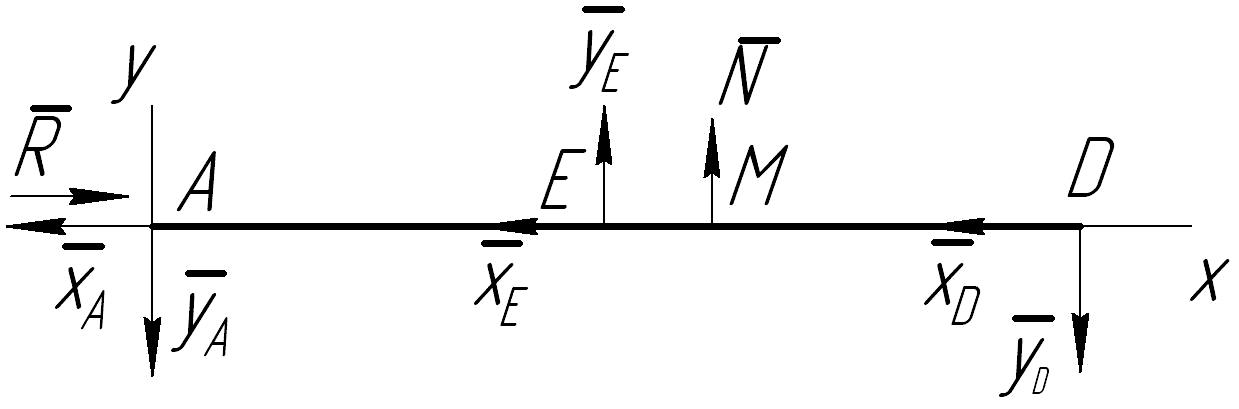
Рис.2.16. Расчетная схема

Составим уравнения равновесия:

(2.13)

(2.14)

. (2.15)

Решаем полученную систему уравнений (2.4)-(2.15). Из уравнения (2.9) имеем:

.

Из уравнения (2.8):

.

Из уравнения (2.6):

.

Из уравнения (2.4) имеем:

.

Из уравнения (2.11):

.

Из уравнения (2.12):

.

Из уравнения (2.10):

.

Из уравнения (2.7):

.

Из уравнения (2.5):

.

Из уравнения (2.13):

.

Из уравнения (2.14):

.

Таким образом, определены все составляющие реакции в шарнирах секции механизированной крепи.

Для проверки найденных величин воспользуемся уравнением (2.15)